Come determinare l'equazione dell'ellisse nota l'eccentricità e un fuoco
Per determinare l'equazione dell'ellisse con centro nell'origine, data l'eccentricità \( e = \frac{2 \sqrt{5}}{5} \) e le coordinate di un fuoco, seguo questi passaggi:
- Il fuoco mi permette di individuare l'asse maggiore dell'ellisse
- Se l'asse maggiore è orizzontale (a>b) la formula dell'eccentricità è $$ e= \frac{c}{a} $$ altrimenti, se è verticale (a<b) è $$ e= \frac{c}{b} $$
- La formula dell'eccentricità mi permette di trovare la lunghezza del semiasse maggiore
- Una volta trovata la lunghezza del semiasse maggiore, calcolo quella del semiasse minore in base alla relazione $ c= \sqrt{a^2 - b^2} $ se l'asse maggiore è orizzontale (a>b) oppure $ c= \sqrt{b^2 - a^2} $ se l'asse maggiore è verticale (a<b).
Un esempio pratico
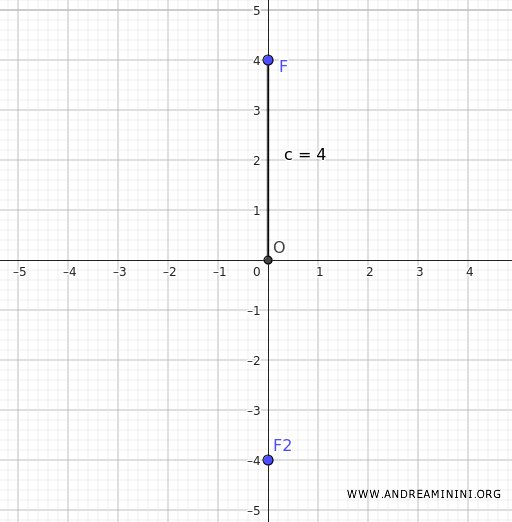
Considero un'ellisse con centro nell'origine, un'eccentricità \( e = \frac{2 \sqrt{5}}{5} \) e un fuoco nel punto \((0, 4)\).
I fuochi di un'ellisse centrata nell'origine sono simmetrici rispetto all'origine. Quindi, se un fuoco si trova in \((0, 4)\), l'altro fuoco sarà in \((0, -4)\).

Sapendo che i fuochi si trovano sempre sull'asse maggiore, deduco che in questa ellisse l'asse maggiore è verticale.
La distanza tra i due fuochi \(2c\) è uguale alla distanza tra i due punti \((0, 4)\) e \((0, -4)\)) ed è uguale a 8
$$ 2c = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} $$
$$ 2c = \sqrt{(0-0)^2+(4-(-4))^2} $$
$$ 2c = \sqrt{8} $$
Quindi, se \(2c = 8\) allora la distanza tra il centro e un fuoco è la metà ovvero \(c = 4\).
$$ c=4 $$
Quando l'asse maggiore è verticale, l'eccentricità \(e\) è definita come \(e = \frac{c}{b}\), dove \(b\) è il semiasse maggiore.
$$ e = \frac{c}{b} $$
Dato \(e = \frac{2 \sqrt{5}}{5}\) e \(c = 4\), posso calcolare \(b\):
$$ \frac{2 \sqrt{5}}{5} = \frac{c}{b} $$
$$ \frac{2 \sqrt{5}}{5} = \frac{4}{b} $$
$$ b = \frac{4 \cdot 5}{2 \sqrt{5}} $$
$$ b = \frac{20}{2 \sqrt{5}} $$
$$ b = \frac{10}{\sqrt{5}} $$
$$ b = 2\sqrt{5} $$
A questo punto, trovo il semiasse minore \(a\) sapendo che nelle ellissi in cui l'asse maggiore è verticale (b>a) vale la relazione:
$$ c = \sqrt{b^2 - a^2 } $$
Dove \(b = 2\sqrt{5}\) e \(c = 4\):
$$ 4 = \sqrt{(2\sqrt{5})^2 - a^2 } $$
$$ 4 = \sqrt{(4 \cdot 5 - a^2 } $$
$$ 4 = \sqrt{(20 - a^2 } $$
Elevo al quadrato entrambi i lati dell'equazione
$$ (4)^2 = ( \sqrt{(20 - a^2 } )^2 $$
$$ 16 = 20 - a^2 $$
$$ a^2= 20 - 16 $$
$$ a^2 = 4 $$
$$ \sqrt{a^2} = \sqrt{4} $$
$$ a=2 $$
Quindi, il semiasse minore orizzontale è lungo 2.
A questo punto, noti $ a= 2 $ e $ b = 2\sqrt{5} $ posso scrivere l'equazione dell'ellisse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{(2\sqrt{5})^2} = 1 $$
$$ \frac{x^2}{e} + \frac{y^2}{4 \cdot 5} = 1 $$
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
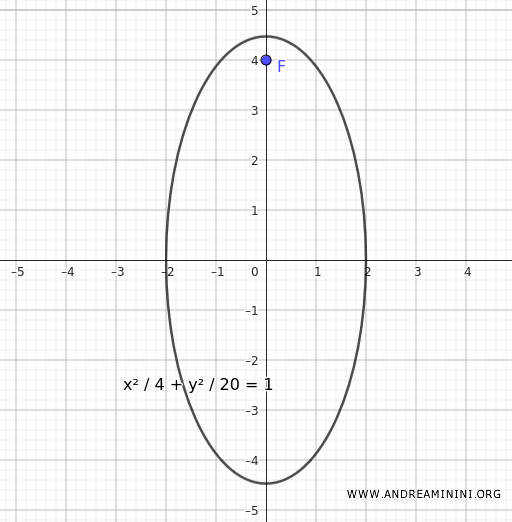
Quindi, l'equazione dell'ellisse è:
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
Ecco la rappresentazione grafica:
E così via.
