Come determinare l'equazione dell'ellisse dato un punto e un vertice
Per scrivere l'equazione di un'ellisse centrata nell'origine degli assi, noto un vertice e un punto, sostituisco i dati nell'equazione generale $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Un esempio pratico
Considero un'ellisse centrata nell'origine $ O(0;0) $ con un vertice alle coordinate $ V(-3;0) $ e passante per il punto $ P ( - \frac{ 3\sqrt{2} }{2}; -2 ) $
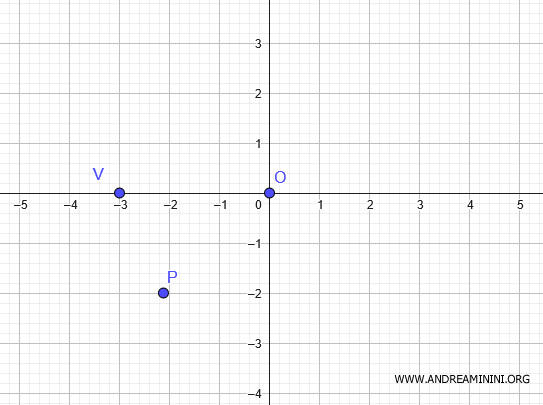
Il vertice $ V(-3;0) $ si trova sull'asse delle x.
Poiché i vertici sono simmetrici rispetto all'origine, deduco che l'altro vertice orizzontale sia $ V(3;0)$
La distanza tra il vertice $ V(-3;0) $ e l'origine $ O(0;0) $ misura la lunghezza del semiasse orizzontale.
$$ a = \sqrt{(x_v - x_o)^2 + (y_v-y_o)^2} $$
$$ a = \sqrt{(-3 - 0)^2 + (0-0)^2} $$
$$ a = \sqrt{9} $$
$$ a = 3 $$
Scrivo l'equazione generale dell'ellisse.
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} $$
Sostituisco il dato sulla lunghezza del semiasse orizzontale $ a=3 $
$$\frac{x^2}{3^2} + \frac{y^2}{b^2} = 1 $$
$$\frac{x^2}{9} + \frac{y^2}{b^2} = 1 $$
Sostituisco $ x $ e $ y $ con le coordinate del punto $ P ( - \frac{ 3\sqrt{2} }{2}; -2 ) $
$$\frac{( - \frac{ 3\sqrt{2} }{2} )^2}{9} + \frac{(-2)^2}{b^2} = 1 $$
$$\frac{ \frac{ 9 \cdot 2 }{4} }{9} + \frac{4}{b^2} = 1 $$
$$\frac{ \frac{ 18 }{4} }{9} + \frac{4}{b^2} = 1 $$
$$\frac{ \frac{ 9 }{2} }{9} + \frac{4}{b^2} = 1 $$
$$ \frac{ 9 }{2} \cdot \frac{1}{9} + \frac{4}{b^2} = 1 $$
$$ \frac{1}{2} + \frac{4}{b^2} = 1 $$
Ricavo la variabile $ b $ ovvero la lunghezza dell'altro semiasse.
$$ \frac{4}{b^2} = 1 - \frac{1}{2} $$
$$ \frac{4}{b^2} = \frac{1}{2} $$
$$ b^2 =2 \cdot 4 $$
$$ b^2 =8 $$
$$ b = \sqrt{8} $$
$$ b =2 \sqrt{2} $$
Poiché $ a > b $ l'asse maggiore dell'ellisse è orizzontale.
Una volta trovate le lunghezze dei semiassi $ a=3 $ e $ b = 2 \sqrt{2} $ li sostituisco nell'equazione generale dell'ellisse
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$\frac{x^2}{3^2} + \frac{y^2}{( 2 \sqrt{2}) ^2} = 1 $$
$$\frac{x^2}{9} + \frac{y^2}{( 4 \cdot 2 } = 1 $$
$$\frac{x^2}{9} + \frac{y^2}{8} = 1 $$
$$ \frac{8x^2+9y^2}{72} = 1 $$
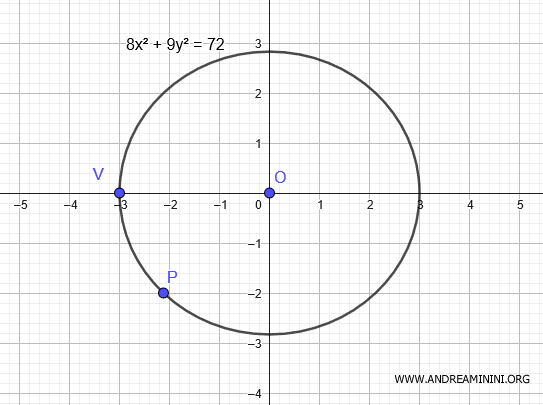
$$ 8x^2+9y^2 = 72 $$
Questa è l'equazione dell'ellisse centrata nell'origine $ O(0;0) $ con un vertice in $ V(-3;0) $ e passante per il punto $ P ( - \frac{ 3\sqrt{2} }{2}; -2 ) $
E così via.
