Come determinare l'equazione di una ellisse dato un fuoco e un vertice
Per determinare l'equazione dell'ellisse centrata nell'origine dato un vertice e un fuoco, ricavo la lunghezza del semiasse mancante usando il teorema di Pitagora.
In un'ellisse si forma un triangolo tra l'origine, un fuoco e un vertice (OF2B2).
In questo triangolo un cateto $ c $ è la distanza del fuoco dal centro, l'altro cateto $ b $ è il semiasse minore dell'ellisse mentre l'ipotenusa $ d=a $ è uguale al semiasse maggiore $ a $ dell'ellisse.
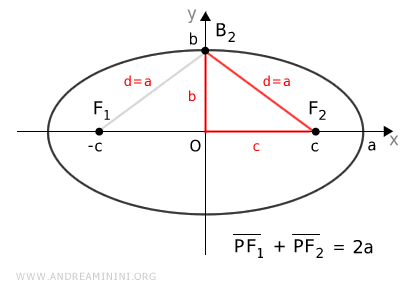
Quindi, per conoscere la lunghezza del semiasse mancante dell'ellisse, basta utilizzare il teorema di Pitagora.
Nota. La conoscenza del centro è essenziale per risolvere il problema. La sola conoscenza del vertice e del fuoco senza conoscere anche il centro non permette di risolverlo. In questo caso l'ipotesi iniziale è quella di avere un'ellisse centrata sull'origine degli assi cartesiani $ O(0;0) $.
Un esempio pratico
Considero un'ellisse centrata nell'origine \((0,0)\), un vertice \( V(5,0)\) e un fuoco \( F(4,0)\).
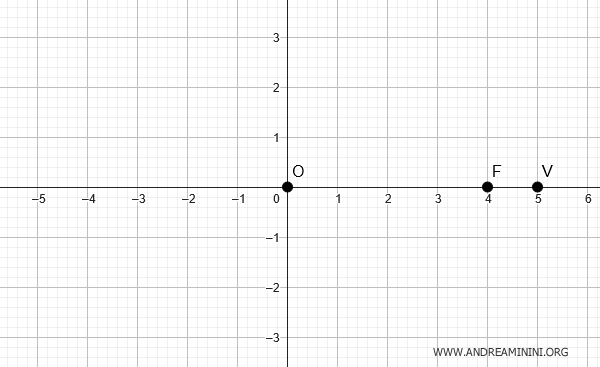
Devo determinare l'equazione dell'ellisse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Dove $ a $ è la lunghezza del semiasse sulle x mentre $ b $ è quella del semiasse sulle y.
Il fuoco \( F(4,0)\) e il vertice \( V(5,0)\) si trovano sull'asse delle x. Questo significa che l'asse maggiore dell'ellisse è orizzontale.
Inoltre, la lunghezza del semiasse orizzontale $ a $ è uguale alla distanza tra il centro \((0,0)\) e il vertice \( V(5,0)\)
$$ a = \sqrt{ (x_v-x_o)^2 - (y_v-y_o)^2 } $$
$$ a = \sqrt{ (5-0)^2 - (0-0)^2 } $$
$$ a = \sqrt{ 25 } $$
$$ a = 5 $$
Quindi, la lunghezza del semiasse orizzontale è $ a = 5 $
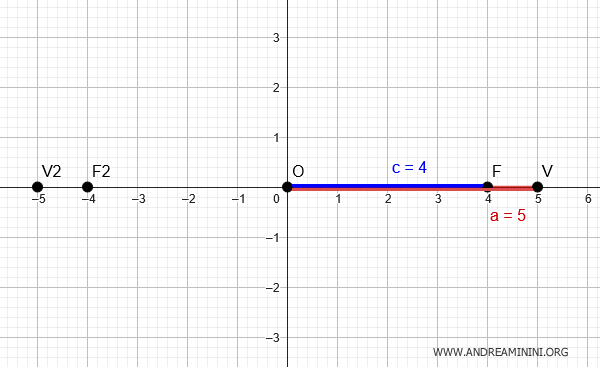
Inoltre, dalle informazioni fornite la distanza dal centro a ciascun fuoco è \(c = 4\).
Nota. Uno dei fuochi è \((4,0)\), il che implica che l'altro fuoco è \((-4,0)\) poiché i fuochi sono simmetrici rispetto all'origine. Inoltre, se uno dei vertici è \((5,0)\), questo implica che l'altro vertice è \((-5,0)\) poiché anche i vertici sono simmetrici rispetto all'origine.
Sapendo che la lunghezza del semiasse maggiore $ a $ è uguale al segmento tra il fuoco \(F(4,0)\) e il vertice $ B $ sul semiasse minore, per trovare la lunghezza del semiasse minore $ b $ mi basta applicare il teorema di Pitagora.
$$ c^2 = a^2 - b^2 $$
Sapendo che $ c = 4 $ e $ a = 5 $
$$ 4^2 = 5^2 - b^2 $$
$$ 16 = 25 - b^2 $$
$$ b^2 = 25 -16 $$
$$ b^2 = 9 $$
$$ b = 3 $$
Questo vuole dire che il semiasse verticale misura $ b = 3 $ e gli altri vertici si trovano alle coordinate $ B( 0;3 ) $ e $ B_2( 0;-3 ) $
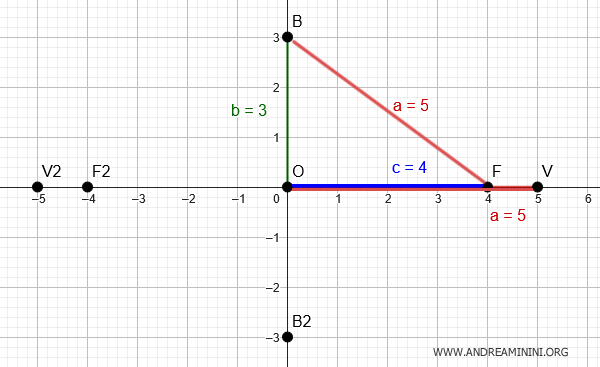
Ora ho tutti i valori necessari $ a=5 $ e $ b=3 $ per scrivere l'equazione dell'ellisse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Ecco la rappresentazione grafica dell'equazione:
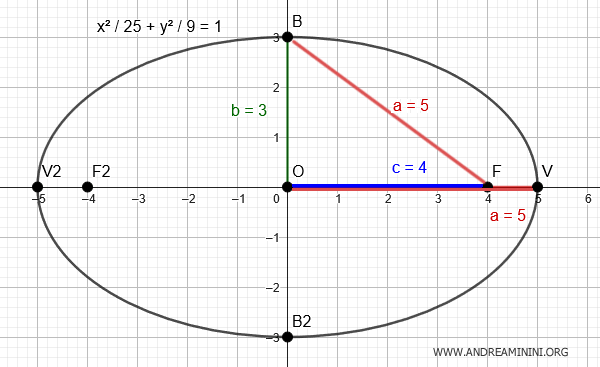
E così via.
