Come trovare l'equazione di un'ellisse dato un punto e un fuoco

Per trovare l'equazione di un'ellisse centrata nell'origine degli assi cartesiani, avendo a disposizione le coordinate di un fuoco $ F(c;0) $ o $ F(0;c) $ e di un punto $ P(x;y) $ appartenente all'ellisse, devo costruire un sistema di equazioni per trovare i valori esatti di \( a \) e \( b \).

La prima equazione la ottengo sostituendo le coordinate del punto  $ P(x;y) $ nell'equazione

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

La seconda equazione dipende dall'orientamento dell'asse maggiore che deduco dalle coordinate del fuoco.

• Se l'asse maggiore è orizzontale utilizzo la relazione tra i semiassi e il fuoco $$ c = \sqrt{a^2-b^2} $$
• Se l'asse maggiore è verticale utilizzo la relazione tra i semiassi e il fuoco $$ c = \sqrt{b^2-a^2} $$

La soluzione del sistema di equazioni mi permette di trovare la lunghezza dei semiassi $ a $ e $ b $ e di completare l'equazione dell'ellisse.

Come capire qual'è l'asse maggiore?  Si capisce dalle coordinate del fuoco. Se il fuoco ha coordinate (c, 0), l'asse maggiore è orizzontale (lungo l'asse x). Viceversa, se il fuoco ha coordinate (0, c), l'asse maggiore è verticale (lungo l'asse y).

Un esempio pratico

Devo trovare l'equazione di un'ellisse centrata nell'origine degli assi cartesiani che ha un fuoco in $ F(0; 2 \sqrt{2}) $ e passa per il punto $ P( \frac{ \sqrt{5} }{3}; 2 ) $

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

L'ellisse ha l'asse maggiore verticale perché il fuoco $ F(0; 2 \sqrt{2}) $ si trova sull'asse delle ordinate y.

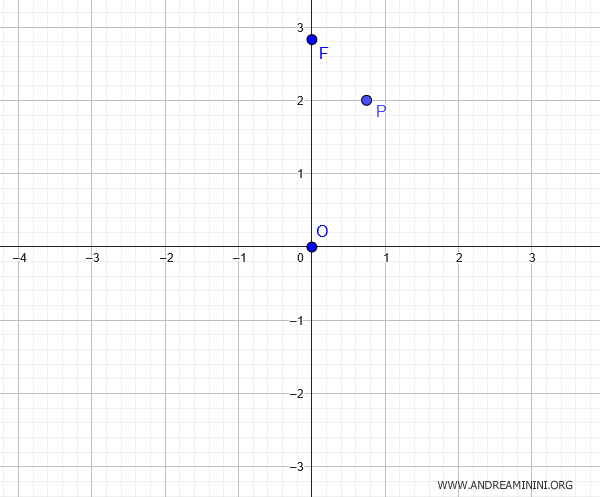
Quando l'asse maggiore è verticale, la relazione tra i semiassi è la seguente:

$$ c = \sqrt{b^2 - a^2} $$

Poiché conosco già le coordinate del fuoco $ F(0; 2 \sqrt{2}) $, la cui componente sulle ordinate è $ c = 2 \sqrt{2} $  posso scrivere

$$ 2 \sqrt{2} = \sqrt{b^2 - a^2} $$

$$ (2 \sqrt{2})^2 = ( \sqrt{b^2 - a^2})^2 $$

$$ 4 \cdot 2 = b^2 - a^2 $$

$$ 8 = b^2 - a^2 $$

Questa è una delle prime equazioni del sistema che mi aiuteranno a risolvere il problema.

L'altra equazione la ottengo sostituendo le coordinate del punto $ P( \frac{ \sqrt{5} }{3}; 2 ) $ nell'equazione dell'ellisse

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{( \frac{ \sqrt{5} }{3} )^2}{a^2} + \frac{2^2}{b^2} = 1 $$

$$ \frac{ \frac{ 5 }{9} }{a^2} + \frac{4}{b^2} = 1 $$

$$  \frac{ 5 }{9} \cdot \frac{1 }{a^2} + \frac{4}{b^2} = 1 $$

$$  \frac{ 5 }{9a^2}  + \frac{4}{b^2} = 1 $$

A questo punto costruisco il sistema di equazioni

$$ \begin{cases} b^2 - a^2 = 8 \\ \\ \frac{ 5 }{9a^2}  + \frac{4}{b^2} = 1 \end{cases} $$

Sostituisco $ b^2 = 8+a^2 $ nella seconda equazione.

$$ \begin{cases} b^2  = 8+a^2 \\ \\ \frac{ 5 }{9a^2}  + \frac{4}{8+a^2} = 1 \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ \frac{ 5 }{9a^2}  + \frac{4}{8+a^2} - 1 = 0 \end{cases} $$

La seconda equazione è un'equazione fratta. Per semplificarla, moltiplico ogni termine per  $ 9a^2(8+a^2) $

$$ \begin{cases} b^2  = 8+a^2 \\ \\ ( \frac{ 5 }{9a^2} + \frac{4}{8+a^2}- 1 ) \cdot [9a^2(8+a^2) ] = 0 \cdot [9a^2(8+a^2) ] \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ 5 \cdot (8+a^2)   + 4 \cdot 9a^2 - 9a^2(8+a^2)  = 0  \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ 40+5 a^2   + 36 a^2 - 72a^2-9a^4  = 0  \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ 40 + a^2 (5+36-72) -9a^4 = 0  \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ 40 - 31 a^2 -9a^4 = 0  \end{cases} $$

$$ \begin{cases} b^2  = 8+a^2 \\ \\ 9a^4 + 31a^2 - 40 = 0  \end{cases} $$

Per risolvere l'equazione di 4° introduco una variabile ausiliaria $ k =a^2 $

$$ 9a^4 + 31a^2 - 40 = 0 $$

$$ 9k^2 + 31k - 40 = 0 $$

In questo modo posso risolvere l'equazione per $ k $ usando la formula delle equazioni di 2° grado.

$$ k = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Dove \( a = 9 \), \( b = 31 \), e \( c = -40 \).

$$ k = \frac{-31 \pm \sqrt{31^2 - 4 \cdot 9 \cdot (-40)}}{2 \cdot 9} $$

$$ k = \frac{-31 \pm \sqrt{961 + 1440}}{18} $$

$$ k = \frac{-31 \pm \sqrt{2401}}{18} $$

$$ k = \frac{-31 \pm 49}{18} $$

Calcolo le soluzioni per \( k \) (cioè \( a^2 \))

$$ k = \begin{cases}  \frac{-31 - 49}{18} = - \frac{80}{18} = - \frac{40}{9} \\ \\ \frac{-31+ 49}{18} = \frac{18}{18} = 1   \end{cases} $$

Le soluzioni per \( k \) (cioè \( a^2 \)) dall'equazione quadratica sono \( k = -\frac{40}{9} \) e \( k = 1 \).

Dato che \( k \) rappresenta \( a^2 \), accetto solo la soluzione positiva \( k = 1 \).

$ k = 1 $

Sapendo che la variabile ausiliaria è $ k = a^2 $

$$ a^2 = 1  $$

Calcolo la radice quadrata a entrambi i membri

$$ \sqrt{a^2} = \sqrt{1} $$

$$ a = 1 $$

Una volta trovato il valore $ a = 1 $ lo sostituisco nella prima equazione $ b^2  = 8+a^2 $ del sistema per trovare anche il valore della variabile $ b $

$$ \begin{cases} b^2  = 8+a^2 \\ \\ a = 1  \end{cases} $$

$$ \begin{cases} b^2  = 8+1^2 \\ \\ a = 1  \end{cases} $$

$$ \begin{cases} b^2  = 9 \\ \\ a = 1  \end{cases} $$

$$ \begin{cases} b  =3 \\ \\ a = 1  \end{cases} $$

Le soluzioni per il sistema di equazioni sono $  a = 1 $ e $  b = 3 $.

Questo mi porta all'equazione dell'ellisse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{1} + \frac{y^2}{3^2} = 1 $$

$$ x^2+ \frac{y^2}{9} = 1 $$

Questa è l'equazione finale dell'ellisse centrata nell'origine con i dati forniti.

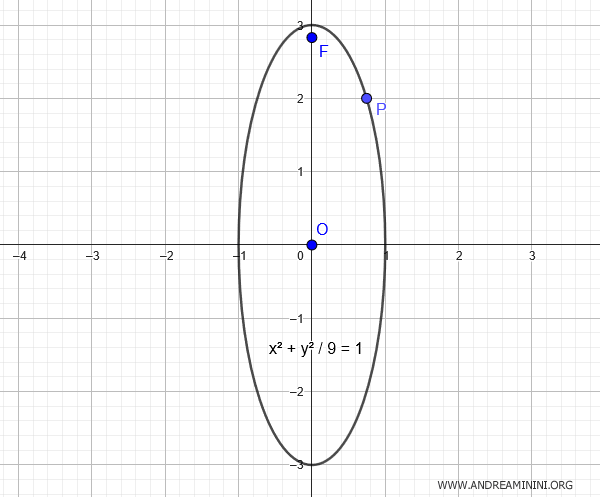
E così via.