Come ottenere l'equazione dell'ellisse dati i due semiassi

Quando sono note le lunghezze dei due semiassi di un'ellisse, l'equazione dell'ellisse può essere determinata facilmente. Ci sono due casi principali da considerare:

• Ellisse centrata nell'origine (0, 0)
  Se l'ellisse è centrata nell'origine degli assi cartesiani l'equazione dell'ellisse si ottiene semplicemente indicando la lunghezza \(a\) del semiasse orizzontale e la lunghezza \(b\) del semiasse verticale. $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
• Ellisse traslata in un punto \((h, k)\)
  Se l'ellisse è centrata in un punto $ P(h,k) $ l'equazione dell'ellisse è: $$ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 $$ Dove \( a \) è la lunghezza del semiasse orizzontale e \( b \) quella del semiasse verticale.

Esempio pratico

Considero un'ellisse centrata nell'origine con il semiasse orizzontale \(a = 5\) e il semiasse verticale \(b = 3\).

L'equazione dell'ellisse è:

$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$

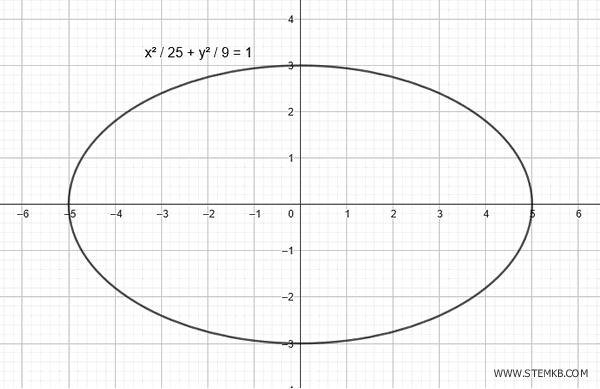
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

Ecco il grafico dell'ellisse

Se invece l'ellisse è centrata nel punto \((2, -1)\) con gli stessi semiassi, l'equazione è:

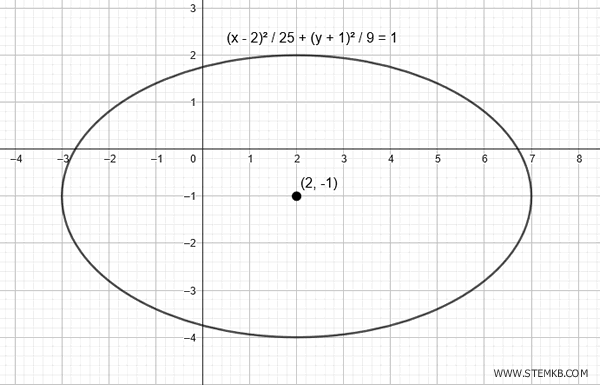
$$ \frac{(x - 2)^2}{25} + \frac{(y + 1)^2}{9} = 1 $$

Questo è il grafico dell'ellisse traslata

Queste formule generali possono essere applicate a qualsiasi ellisse di cui siano note le lunghezze dei semiassi e la posizione del centro.

E così via.