Come determinare l'equazione dell'ellisse nota l'eccentricità e un vertice

Per ottenere l'equazione di un'ellisse centrata nell'origine $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ conoscendo un vertice $ V(x_v;y_v) $ e l'eccentricità $ e $ devo capire se l'asse maggiore è orizzontale o verticale

• Se l'asse maggiore è orizzontale (a>b) utilizzo la formula dell'eccentricità $ e = \frac{c}{a} $ e la relazione $ c^2 = a^2-b^2 $
• Se l'asse maggiore è verticale (b>a) utilizzo la formula dell'eccentricità $ e = \frac{c}{b} $ e la relazione $ c^2 = b^2-a^2 $

La conoscenza del vertice $ V(x_v;y_v) $ mi permette di conoscere la lunghezza di un semiasse orizzontale o verticale.

Quando il problema non indica il semiasse maggiore, vanno considerate entrambe le ipotesi.

Un esempio pratico

Un'ellisse centrata nell'origine ha un vertice in \((-3,0)\) e \(e= \frac{\sqrt{7}}{3}\)

La conoscenza di un vertice senza altre informazioni non mi permette di capire qual'è l'asse maggiore.

Quindi, devo considerare due ipotesi: l'asse maggiore è orizzontale oppure verticale.

1] L'asse maggiore è orizzontale

In questa ipotesi il semiasse maggiore \(a\) è quello maggiore, ovvero quello in cui risiedono i fuochi dell'ellisse.

In un'ellisse centrata nell'origine se il vertice è \((-3,0)\) allora uno dei semiassi ha lunghezza $ a=3 $.

Quando il semiasse maggiore \(a\) è 3, la formula dell'eccentricità \(e\) è $ e=\frac{c}{a} $:

$$ e = \frac{c}{a} = \frac{\sqrt{7}}{3} $$

Questo vuole dire che la distanza dal centro ai fuochi è $ c= \sqrt{7} $

Quando l'asse maggiore è orizzontale vale la relazione \(c^2 = a^2 - b^2\)

$$ c^2 = a^2 - b^2 $$

Sapendo che $ a=3 $ e $ c= \sqrt{7} $

$$ (\sqrt{7})^2 = 3^2 - b^2 $$

$$ 7 = 9 - b^2 $$

$$ b^2 = 9 - 7 $$

$$ b^2 = 2 $$

$$ b = \sqrt{2} $$

A questo punto ho sia la lunghezza del semiasse maggiore $ a = 3 $ che quella del semiasse minore $ b = \sqrt{2} $

Sostituendo \(a\) e \(b\) nell'equazione standard dell'ellisse ottengo l'equazione dell'ellisse.

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} + \frac{y^2}{( \sqrt{2} )^2} = 1 $$

$$ \boxed{\frac{x^2}{9} + \frac{y^2}{2} = 1} $$

Questa è l'equazione dell'ellisse con un vertice in \( (-3;0) \) e una eccentricità \( e= \frac{\sqrt{7}}{3} \) quando l'asse maggiore è orizzontale.

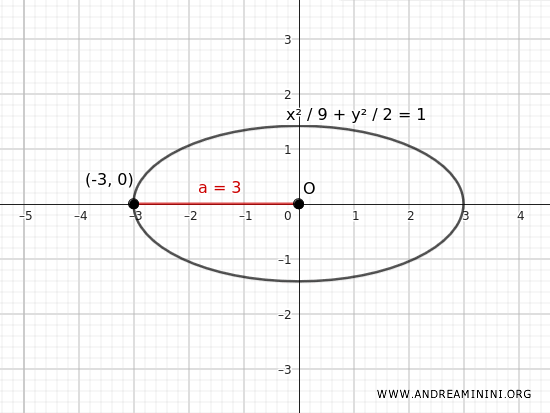
Nota. Con i semiassi $ a=3 $ e $ b = \sqrt{2} $ e la distanza focale $ c= \sqrt{7} $ l'eccentricità è rispettata $$ e = \frac{c}{a} = \frac{ \sqrt{7 }}{3 } $$

2] L'asse maggiore è verticale

In questa ipotesi il semiasse maggiore \(b\) è quello maggiore, ovvero l'asse verticale è quello in cui risiedono i fuochi dell'ellisse.

Dai dati del problema conosco la lunghezza del semiasse orizzontale minore ossia $ a=3 $

Quando l'asse maggiore è verticale la formula dell'eccentricità è $ e = \frac{c}{b} $ e la relazione tra gli assi è $ c^2 = b^2 - a^2 $

$$ e = \frac{c}{b} = \frac{\sqrt{7}}{3} $$

Dove $ c^2 = b^2 - a^2 $ quindi $ c = \sqrt{b^2-a^2} $$

$$  \frac{\sqrt{b^2-a^2}}{b} = \frac{\sqrt{7}}{3} $$

Sapendo che il semiasse orizzontale minore è $ a=3  $

$$  \frac{\sqrt{b^2-3^2}}{b} = \frac{\sqrt{7}}{3} $$

$$  \frac{\sqrt{b^2-9}}{b} = \frac{\sqrt{7}}{3} $$

$$  \sqrt{b^2-9} = \frac{\sqrt{7}}{3} b $$

Elevo al quadrato entrambi i lati

$$ (  \sqrt{b^2-9} )^2 = ( \frac{\sqrt{7}}{3} b )^2 $$

$$ b^2-9 = \frac{7}{9} b^2 $$

$$ b^2- \frac{7}{9} b^2 = 9  $$

$$ \frac{9b^2 - 7b^2}{9}  = 9  $$

$$ \frac{2b^2}{9}  = 9  $$

$$ b^2  = \frac{ 9 \cdot 9 }{2} $$

$$ b^2  = \frac{ 81 }{2} $$

Calcolo la radice quadrata in entrambi i lati dell'equazione

$$ \sqrt{b^2} = \sqrt{ \frac{ 81 }{2} } $$

$$ b =  \frac{ 9 }{\sqrt{2} } $$

Moltiplico e divido il secondo membro per $ \sqrt{2} $ per portare il radicale al numeratore

$$ b =  \frac{ 9 }{\sqrt{2} } \cdot \frac{\sqrt{2}}{\sqrt{2}} $$

$$ b =  \frac{ 9 \sqrt{2} }{2 } $$

A questo punto conosco la lunghezza sia del semiasse minore $ a=3 $ che quella del semiasse maggiore $ b =  \frac{ 9 \sqrt{2} }{2 } $

Sostituisco $ a $ e $ b $ nell'equazione dell'ellisse.

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} + \frac{y^2}{( \frac{ 9 \sqrt{2} }{2 })^2} = 1 $$

$$ \frac{x^2}{9} + \frac{y^2}{ \frac{ 81}{2} } = 1 $$

$$ \frac{x^2}{9} + y^2 \cdot  \frac{ 2}{81}   = 1 $$

$$ \boxed{ \frac{x^2}{9} +  \frac{ 2y^2}{81}   = 1 } $$

Questa è l'equazione dell'ellisse con un vertice in \( (-3;0) \) e una eccentricità \( e= \frac{\sqrt{7}}{3} \) quando l'asse maggiore è verticale.

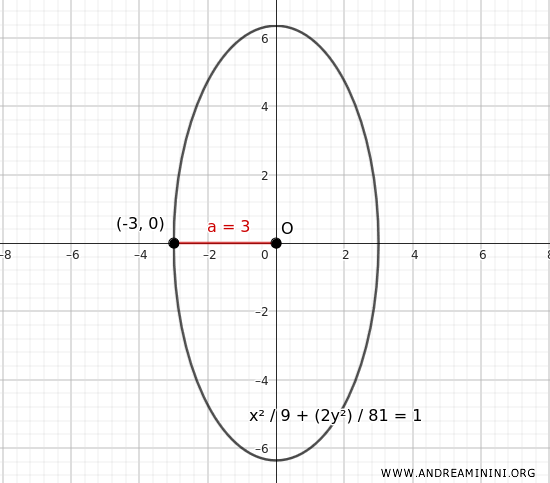
Nota. Con i semiassi $ a=3 $ e $ b= \frac{ 9 \sqrt{2} }{2 } $ l'eccentricità è rispettata $$ e = \frac{c}{b} = \frac{c}{  \frac{ 9 \sqrt{2} }{2 } } $$ Sapendo che $ c^2 = b^2-a^2 $ allora $ c = \sqrt{b^2-a^2} $ $$ e = \frac{ \sqrt{b^2-a^2}}{  \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{( \frac{ 9 \sqrt{2} }{2 } )^2-3^2}}{  \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{  \frac{ 81 }{2 }-9 }}{  \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{   \sqrt{ \frac{ 81-18 } {2 }}}{  \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{  \sqrt{  \frac{  63 }{2 }}}{  \frac{ 9 \sqrt{2} }{2 } } $$ $$ e =    \frac{ \sqrt{63} }{\sqrt{2} } \cdot \frac{ 2 }{9 \sqrt{2} }  $$ $$ e =    \frac{ \sqrt{7 \cdot 3^2} }{2 } \cdot \frac{ 2 }{9 \sqrt{2} }  $$ $$ e =    \frac{ 3 \sqrt{7} }{ \sqrt{2} } \cdot \frac{\sqrt{2}}{ \sqrt{2}} \cdot \frac{ 2 }{9 \sqrt{2} }  $$ $$ e =    \frac{ 3 \sqrt{14} }{2 } \cdot \frac{ 2 }{9 \sqrt{2} }  $$ $$ \require{cancel} e =    \frac{ 3 \sqrt{14} }{ \cancel{2} } \cdot \frac{ \cancel{2} }{9 \sqrt{2} }  $$ $$ e =    \frac{ \sqrt{14} }{ 3 \sqrt{2} }  $$ $$ e = \frac{1}{3} \cdot  \frac{ \sqrt{14} }{ \sqrt{2} }  $$ $$ e = \frac{1}{3} \cdot  \sqrt{ \frac{14}{2}}  $$ $$ e = \frac{1}{3} \cdot  \sqrt{ 7 }  $$ $$ e = \frac{ \sqrt{ 7 } }{3}    $$

In conclusione, senza ulteriori informazioni, entrambe le equazioni sono valide soluzioni per l'ellisse.

E così via.