Retta secante, tangente o esterna a un'ellisse
Sul piano una retta può essere secante, tangente o esterna a un'ellisse
- E' secante se ha due punti in comune con l'ellisse
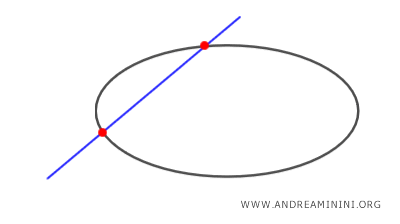
- E' tangente se ha un solo punto in comune con l'ellisse
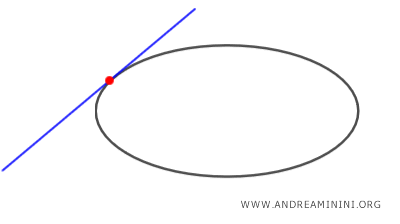
- E' esterna se non ha punti in comune con l'ellisse
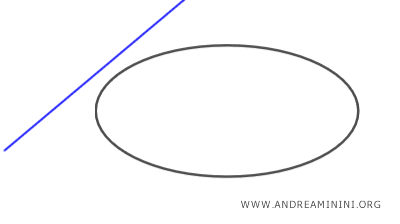
Per trovare i punti di intersezione in comune devo risolvere il sistema composto dall'equazione della retta e dall'equazione dell'ellisse.
Se il sistema ha due soluzioni reali distinte, la retta è secante. Se ha una soluzione reale è tangente e se non ha nessuna è esterna.
Nota. Per trovare l'equazione della retta tangente in un punto dell'ellisse specifico posso anche usare la formula di sdoppiamento.
Un esempio pratico
Considero l'ellisse
$$ x^2 + 4y^2 = 40 $$
e una retta
$$ x+6y-20=0 $$
Devo scoprire se la retta è secante, tangente o esterna.
Metto a sistema le due equazioni.
$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x+6y-20=0 \end{cases} $$
Cerco di risolvere il sistema con il metodo della sostituzione.
$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x=20-6y \end{cases} $$
$$ \begin{cases} (20-6y)^2 + 4y^2 = 40 \\ \\ x=20-6y \end{cases} $$
$$ \begin{cases} 400 - 240y + 36y^2 + 4y^2 - 40 = 0 \\ \\ x=20-6y \end{cases} $$
$$ \begin{cases} 40y^2 - 240y +360 = 0 \\ \\ x=20-6y \end{cases} $$
Semplifico la prima equazione dividendo entrambi i membri per dieci e poi per quattro.
$$ \begin{cases} 4y^2 - 24y + 36 = 0 \\ \\ x=20-6y \end{cases} $$
$$ \begin{cases} y^2 - 6y + 9 = 0 \\ \\ x=20-6y \end{cases} $$
L'equazione di 2° grado $ y^2 - 6y + 9 = 0 $ è l'equazione risolvente del sistema. Il discriminante dell'equazione è:
$$ \Delta = b^2 - 4ac $$
$$ \Delta = (-6)^2 - 4 \cdot 1 \cdot 9 $$
$$ \Delta = 36 - 36 $$
$$ \Delta = 0 $$
Il disciminante è zero, quindi il sistema ha una sola soluzione e la retta è tangente all'ellisse.
A questo punto risolvo l'equazione di 2° grado $ y^2 - 6y + 9 = 0 $ per trovare il valore della y.
$$ y = \frac{-b \pm \sqrt{\Delta}}{2a} $$
$$ y = \frac{-(-6) \pm \sqrt{0}}{2 \cdot 1} $$
$$ y = \frac{6}{2} $$
$$ y = 3 $$
Una volta trovato il valore della variabile y=3 lo sostituisco nell'equazione della retta per trovare quello della x.
$$ \begin{cases} y = 3 \\ \\ x=20-6 \cdot 3 \end{cases} $$
$$ \begin{cases} y = 3 \\ \\ x=2 \end{cases} $$
Pertanto, il punto di tangenza si trova alle coordinate (2;3).
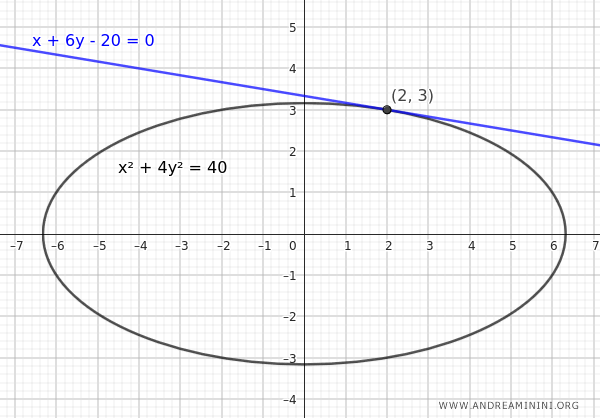
E così via.
