Il metodo del completamento del quadrato in un'ellisse
Il metodo del completamento del quadrato mi permette di determinare le caratteristiche di un'ellisse osservando la sua equazione generale $$ Ax^2 + By^2 + Cx+ Dy + E = 0 $$ raggruppando i termini x e y facendo in modo che in ogni parentesi si formi un binomio di un quadrato, allo scopo di ottenere l'equazione canonica dell'ellisse $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$ Dove $ (x_0;y_0) $ è il centro dell'ellisse.
Un esempio pratico
Considero l'equazione generale di un'ellisse
$$ 25x^2 + 9y^2 - 100x - 18y - 116 = 0 $$
Devo trasformare l'equazione dell'ellisse nella forma canonica $ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $
Sposto il termine noto nel lato destro dell'equazione
$$ 25x^2 + 9y^2 - 100x - 18y = 116 $$
Poi raggruppo x e y
$$ 25 \cdot (x^2 - 4x) + 9 \cdot (y^2-2y) = 116 $$
A questo punto utilizzo il metodo del completamento del quadrato.
Per formare il quadrato del binomio nella prima parentesi, applico la proprietà invariantiva delle equazioni e aggiungo +4·25 in entrambi i lati dell'equazione
$$ 25 \cdot (x^2 - 4x) + 4 \cdot 25 + 9 \cdot (y^2-2y) = 116 + 4 \cdot 25 $$
$$ 25 \cdot (x^2 - 4x + 4) + 9 \cdot (y^2-2y) = 116 + 100 $$
$$ 25 \cdot (x - 2)^2 + 9 \cdot (y^2-2y) = 216 $$
Per formare il quadrato del binomio nella seconda parentesi, aggiungo +1·9 in entrambi i lati dell'equazione.
$$ 25 \cdot (x - 2)^2 + 9 \cdot (y^2-2y) +1 \cdot 9 = 216 +1 \cdot 9 $$
$$ 25 \cdot (x - 2)^2 + 9 \cdot (y^2-2y+1) = 216 +9 $$
$$ 25 \cdot (x - 2)^2 + 9 \cdot (y-1)^2 = 225 $$
Ora divido entrambi i lati dell'equazione per 225
$$ \frac{ 25 \cdot (x - 2)^2 }{225} + \frac{ 9 \cdot (y-1)^2 }{ 225 } = \frac{225}{225} $$
$$ \frac{ 25 \cdot (x - 2)^2 }{225} + \frac{ 9 \cdot (y-1)^2 }{ 225 } = 1 $$
$$ \frac{ (x - 2)^2 }{ \frac{225}{25} } + \frac{ (y-1)^2 }{ \frac{225}{9} } = 1 $$
$$ \frac{ (x - 2)^2 }{ 9 } + \frac{ (y-1)^2 }{ 25 } = 1 $$
Il risultato finale è l'equazione canonica dell'ellisse.
In questa forma deduco immediatamente che l'ellisse è centrata nel punto (2;1)
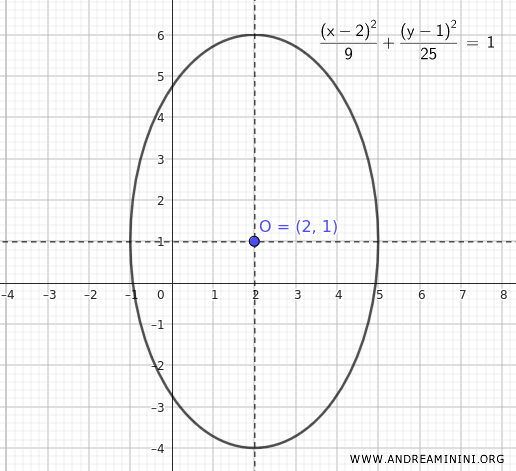
Quindi, gli assi di simmetria dell'ellisse sono $ x=2 $ e $ y=1 $
Inoltre, i termini $ a^2=9 $ e $ b^2=25 $ mi permettono di calcolare le lunghezze dei semiassi $ a=3 $ e $ b= 5 $
In questo caso, essendo $ b > a $ il semiasse maggiore dell'ellisse è quello verticale, parallelo all'asse y.
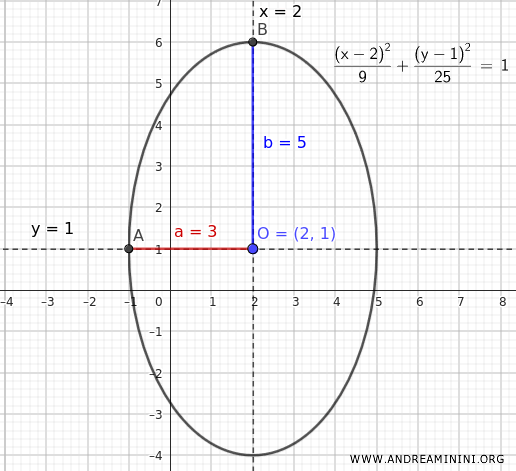
Conoscendo il centro (2;1) e le lunghezze dei semiassi, calcolo facilmente i vertici.
$$ A ( 2 \pm a, 1 ) = (2 \pm 3 , 1 ) = \begin{cases} A_1 ( -1,1) \\ \\ A_2 (5,1) \end{cases} $$
$$ B =(2, 1 \pm b) = (2, 1 \pm 5) = \begin{cases} B_1 ( 2,-4) \\ \\ B_2 (2,6) \end{cases} $$
Infine, noti $ a= 3 $ e $ b= 5 $ posso calcolare la posizione dei fuochi sull'asse verticale, sapendo che quando il semiasse maggiore è verticale vale la relazione $ c^2 = b^2 - a^2 $.
$$ c^2 = b^2 - a^2 $$
$$ c^2 = 5^2 - 3^2 $$
$$ c^2 = 25 - 9 $$
$$ c^2 = 16 $$
$$ \sqrt{c^2} = \sqrt{16} $$
$$ c = 4 $$
Quindi, sull'asse y=1 i fuochi si trovano alle coordinate:
$$ F ( 2, 1 \pm 4 ) = \begin{cases} F_1 ( 2,-3) \\ \\ F_2 (2,5) \end{cases} $$
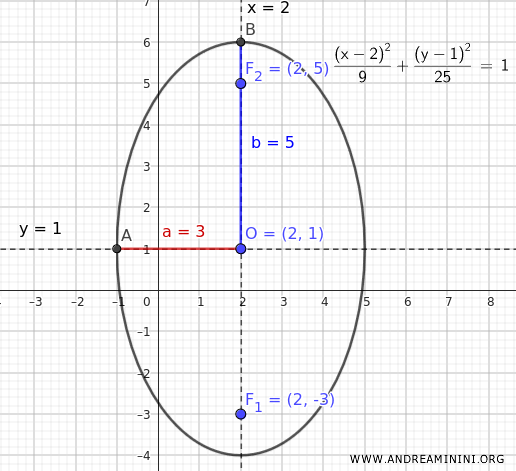
E così via.
