Come determinare l'equazione dell'ellisse noto un punto e l'eccentricità

Per determinare l'equazione di un'ellisse centrata nell'origine date le coordinate di un punto e l'eccentricità dell'ellisse, sostituisco le coordinate del punto nell'equazione generale dell'ellisse

$$ \frac{x^2}{a^2} +  \frac{y^2}{b^2} = 1 $$

Poi a seconda se il semiasse maggiore è orizzontale o verticale considero la formula dell'eccentricità

• Se il semiasse maggiore è orizzontale (a>b)  $$ e= \sqrt{1 - \frac{b^2}{a^2} } $$
• Se il semiasse maggiore è verticale (b>a)  $$ e= \sqrt{1 - \frac{a^2}{b^2} } $$

Metto le due equazioni in un sistema e trovo i dati mancanti.

Nota. Se non conosco qual è l'asse maggiore dell'ellisse, devo considerare entrambe le ipotesi.

Un esempio pratico

Considero una ellisse che passa per il punto \((1, -\sqrt{3})\) e ha come eccentricità \( e = \frac{\sqrt{3}}{3} \) .

Non conosco il semiasse maggiore, quindi devo analizzare entrambe le ipotesi.

1] Primo caso: \(a\) è il semiasse maggiore (a>b)

Quando il semiasse maggiore è orizzontale (a>b) la formula dell'eccentricità è:

$$ e =  \sqrt{1 - \frac{b^2}{a^2}} = \frac{\sqrt{3}}{3} $$

Elevo al quadrato entrambi i lati dell'equazione

$$ (  \sqrt{1 - \frac{b^2}{a^2}} )^2 = ( \frac{\sqrt{3}}{3} )^2 $$

$$  1 - \frac{b^2}{a^2}  = \frac{3}{9} = $$

$$  - \frac{b^2}{a^2}  = \frac{1}{3} - 1 = $$

$$  - \frac{b^2}{a^2}  = \frac{1-3}{3}  = $$

$$  - \frac{b^2}{a^2}  = - \frac{2}{3}  = $$

Moltiplico per -1 entrambi i lati

$$  \frac{b^2}{a^2}  =  \frac{2}{3} $$

$$ b^2  =  \frac{2}{3} a^2 $$

Calcolo la radice quadrata in entrambi i lati dell'equazione

$$ \sqrt{ b^2 }  = \sqrt{  \frac{2}{3} a^2 } $$

$$ b = a \sqrt{\frac{2}{3}} $$

A questo punto sostituisco le coordinate del punto noto \((1, -\sqrt{3})\) nell'equazione generale dell'ellisse.

$$ \frac{x^2}{a^2} +  \frac{x^2}{b^2} = 1 $$

$$  \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Sapendo che $ b = a \sqrt{\frac{2}{3}} $ dalla formula dell'eccentricità, sostituisco $ b $

$$ \frac{1}{a^2} + \frac{3}{(a \cdot \sqrt{ \frac{2}{3} })^2} = 1 $$

$$ \frac{1}{a^2} + \frac{3}{a^2 \cdot \frac{2}{3}} = 1 $$

$$ \frac{1}{a^2} + \frac{3}{\frac{2}{3} a^2} = 1 $$

$$ \frac{1}{a^2} + 3 \cdot \frac{3}{2a^2} = 1 $$

$$ \frac{1}{a^2} + \frac{9}{2 a^2} = 1 $$

$$ \frac{2+9}{2 a^2} = 1 $$

$$ \frac{11}{2 a^2} = 1 $$

$$ 2 a^2 = 11 $$

$$ a^2 = \frac{11}{2} $$

$$ a = \sqrt{\frac{11}{2}} $$

A questo punto, una volta nota la lunghezza di $ a  = \sqrt{\frac{11}{2}} $ calcolo $ b $

$$ b = a \sqrt{\frac{2}{3}} $$

$$ b =  \sqrt{\frac{11}{2}} \sqrt{\frac{2}{3}} $$

$$ b =  \sqrt{ \frac{11}{2} \cdot \frac{2}{3}} $$

$$ b =  \sqrt{ \frac{11}{3} } $$

Quindi, l'equazione dell'ellisse con $ a = \sqrt{\frac{11}{2}} $ e $ b =  \sqrt{ \frac{11}{3} } $ è

$$ \frac{x^2}{a^2} +  \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{( \sqrt{\frac{11}{2}} )^2} +  \frac{y^2}{( \sqrt{ \frac{11}{3} } )^2} = 1 $$

$$ \frac{x^2}{ \frac{11}{2} } +  \frac{y^2}{  \frac{11}{3} } = 1 $$

$$ \frac{2x^2}{ 11 } +  \frac{3y^2}{  11 } = 1 $$

Ecco la rappresentazione grafica:

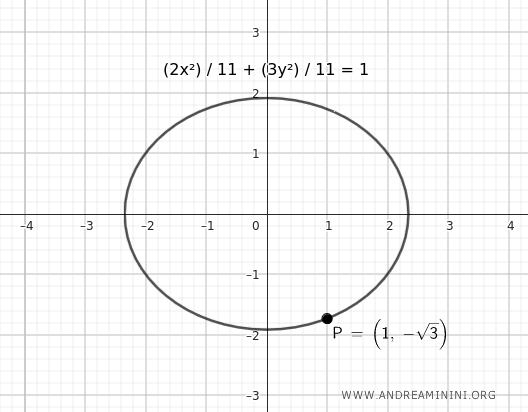
L'ellisse passa per il punto dato.

2] Secondo caso: \(a\) è il semiasse minore (a<b)

Quando $ b $ è il semiasse maggiore la formula dell'eccentricità è $$

$$ e = \sqrt{1 - \frac{a^2}{b^2}} = \frac{\sqrt{3}}{3} $$

Elevo al quadrato entrambi i lati dell'equazione

$$ ( \sqrt{1 - \frac{a^2}{b^2}} )^2 = ( \frac{\sqrt{3}}{3} )^2 $$

$$ 1 - \frac{a^2}{b^2} =\frac{3}{9} $$

$$ 1 - \frac{a^2}{b^2} =\frac{1}{3} $$

$$ - \frac{a^2}{b^2} =\frac{1}{3} - 1 $$

$$ - \frac{a^2}{b^2} =\frac{1-3}{3}  $$

$$ - \frac{a^2}{b^2} =- \frac{2}{3}  $$

Moltiplico entrambi i lati per -1

$$ \frac{a^2}{b^2} = \frac{2}{3}  $$

$$ a = b \sqrt{\frac{2}{3}} $$

A questo punto sostituisco le coordinate del punto noto \((1, -\sqrt{3})\) nell'equazione generale dell'ellisse

$$ \frac{x^2}{a^2} +  \frac{x^2}{b^2} = 1 $$

$$ \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Sapendo che $ a = b \sqrt{\frac{2}{3}} $

$$ \frac{1}{( b \sqrt{\frac{2}{3}} )^2} + \frac{3}{b^2} = 1 $$

$$ \frac{1}{b^2 \cdot \frac{2}{3}} + \frac{3}{b^2} = 1 $$

$$ \frac{3}{2 b^2} + \frac{3}{b^2} = 1 $$

$$ \frac{3+6}{2 b^2}  = 1 $$

$$ \frac{9}{2 b^2}  = 1 $$

$$ 2 b^2 = 9 $$

$$ b^2 = \frac{9}{2} $$

$$ b = \sqrt{\frac{9}{2}} $$

$$ b = \frac{3}{\sqrt{2}} $$

Moltiplico e divido per la radice di due il lato a destra

$$ b = \frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$

$$ b = \frac{3 \sqrt{2}}{2} $$

Una volta ottenuto il valore di $ b = \frac{3 \sqrt{2}}{2} $ posso calcolare $ a$

$$ a = b \sqrt{\frac{2}{3}} $$

$$ a = \frac{3 \sqrt{2}}{2} \cdot \sqrt{\frac{2}{3}} $$

$$ a = \frac{3 \sqrt{2}}{2} \cdot \sqrt{\frac{2}{3}} $$

$$  a = \frac{3 \sqrt{2}}{2} \cdot \frac{\sqrt{2}}{\sqrt{3}} $$

$$ a = \frac{3 \cdot 2}{2 \sqrt{3}} $$

$$ a = \frac{3}{\sqrt{3}} $$

$$ a = \frac{3}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} $$

$$ a = \frac{3 \sqrt{3} }{\sqrt{3} \sqrt{3}}  $$

$$ a = \frac{3 \sqrt{3} }{3}  $$

$$ a = \sqrt{3} $$

A questo punto posso sostituire $ a = \sqrt{3} $ e $ b = \frac{3 \sqrt{2}}{2} $ nell'equazione generale dell'ellisse.

$$ \frac{x^2}{a^2} +  \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{( \sqrt{3} )^2} +  \frac{y^2}{(  \frac{3 \sqrt{2}}{2}  )^2} = 1 $$

$$ \frac{x^2}{3} +  \frac{y^2}{  \frac{9 \cdot 2}{4} } = 1 $$

$$ \frac{x^2}{3} +  \frac{y^2}{  \frac{9}{2} } = 1 $$

$$ \frac{x^2}{3} +  \frac{2y^2}{ 9 } = 1 $$

Questa è l'equazione dell'ellise se \(b\) è il semiasse maggiore.

Ecco la rappresentazione grafica.

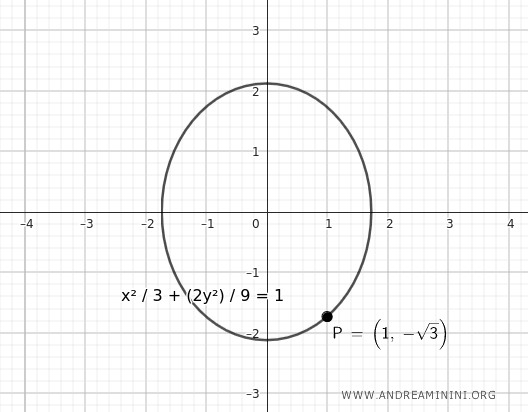
Quindi, l'ellisse che passa per il punto \((1, -\sqrt{3})\) e ha un'eccentricità di \(\frac{\sqrt{3}}{3}\) può essere descritta da una delle due equazioni sopra, a seconda di quale assunzione (semiasse maggiore o minore) sia corretta.

E così via.