Calcolo numerico

Cos'è il calcolo numerico

Il calcolo numerico è una branca della matematica che studia le procedure di risoluzione dei problemi tramite algoritmi computazionali.

A cosa serve?

Il calcolo numerico mi permette di trovare una soluzione approssimata a un problema altrimenti molto difficile o impossibile da trovare tramite l'analisi matematica.

Spesso lo svantaggio dell'approssimazione è compensato dalla rapidità del calcolo.

E' molto utile in ambito ingegneristico e, in generale, in ambito scientifico.

Nota. Il calcolo numerico è usato per risolvere sistemi di equazioni lineari, nella programmazione lineare per minimizzare una funzione lineare condizionata a determinati vincoli, per l'ottimizzazione di una funzione di due o più variabili, nel calcolo differenziale (integrate, derivate, equazioni differenziali).

La differenza tra calcolo numerico e analisi numerica

In alcuni testi il calcolo numerico è detto anche analisi numerica. In realtà, esistono alcune differenze tra i due concetti.

• ll calcolo numerico sviluppa algoritmi di risoluzione dei problemi della matematica del continuo (es. soluzione approssimata di un integrale definito o di una equazione differenziale, ecc.).
• L'analisi numerica, invece, si occupa più propriamente dell'analisi matematica degli algoritmi utilizzati nel calcolo numerico.

Un esempio pratico

Ecco alcune applicazioni pratiche del calcolo numerico

Esempio 1

In molti casi le equazioni differenziali non sono facilmente risolvibili.

Il calcolo numerico mi permette di trovare una soluzione approssimata dell'equazione differenziale che diventa utile se il margine d'errore è accettabile.

Esempio 2

Il calcolo numerico mi permette anche di stimare l'area di una figura senza dover calcolare l'integrale definito.

La discretizzazione del continuo

Spesso il calcolo numerico consiste nella discretizzazione di un problema continuo, ossia nella creazione di un modello a variabili discrete che mi permette di rappresentare lo stesso fenomeno reale in una dimensione numerica finita.

In molti casi un fenomeno reale è rappresentabile tramite un modello matematico.

Il modello matematico è composto da variabili, vincoli, relazioni funzionali e parametri che definiscono il problema.

Il modello matematico è affidabile se è

• ben posto
  fornisce soluzioni uniche e stabile che variano con continuità al variare dei dati. Ad esempio, a parità di condizioni il modello fornisce la stessa risposta.
• ben condizionato
  piccole perturbazioni nei dati in ingresso generano piccole perturbazioni nei risultati in usciti. Ad esempio, l'arrotondamento dei dati non modifica eccessivamente la risposta del modello.

Tuttavia, il modello matematico analizza il problema nella matematica del continuo e questo può appesantire la complessità computazionale della ricerca delle soluzioni.

Per evitare questo handicap posso riscrivere il modello in forma discreta utilizzando valori numerici non continui.

Il modello discreto (o modello numerico) fornisce una risposta approssimata ma in tempi più rapidi.

Nota. Le condizioni di esistenza, di unicità e stabilità delle soluzioni sono soddisfatte anche dal modello discreto. Il modello discreto è comunque ben posto e ben condizionato come il modello continuo. Questo però non vuol dire che sia anche utile. Il modello discreto è accurato ed efficace soltanto se la soluzione approssimata si trova entro un margine di errore accettabile.

Metodi di calcolo numerico

Esistono due metodologie per approcciarsi al calcolo numerico

• Il metodo diretto
  Consiste nell'utilizzo di un algoritmo che fornisce la soluzione entro un numero determinato e finito di passi. Ad esempio il crivello di Eratostene.
• Il metodo iterativo
  Consiste in una sequenza di approssimazioni successive che convergono a una soluzione approssimata finale. Ad esempio, il calcolo di un integrale di una funzione con il metodo dei rettangoli.

Il crivello di Eratostene

Il crivello di Eratostene è un algoritmo usato per calcolare i numeri primi da 1 a N.

Come funziona?

L'algoritmo elenca tutti i numeri naturali da 1 a N.

$$ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 5 \ , \ 6 \ , \ 7 \ , \ 8 \ , \ 9 \ , \ ... \ , \ N $$

Poi elimina i numeri che non sono primi.

Analizza un numero alla volta e lo divide per tutti i numeri precedenti al numero stesso.

• Se il numero analizzato è divisibile per un numero diverso da 1, lo elimina dall'elenco.

  Esempio. L'algoritmo analizza il numero 6. Lo divide per 2 e ottiene un resto pari a zero. Essendo divisibile per due, lo elimina dall'elenco e passa ad analizzare il numero successivo (7).

• Se il numero analizzato è divisibile soltanto per uno, lo mantiene nell'elenco e passa ad analizzare il numero successivo.

  Esempio. L'algoritmo analizza il numero 5. Lo divide per 2 e ottiene un resto r=1 diverso da zero. Lo divide per 3 e ottiene un resto r=2 diverso da zero. Lo divide per 4 e ottiene un resto r=1 diverso da zero. Il numero 5 non è divisibile per nessuno dei numeri precedenti (2,3,4) ad eccezione del numero uno. Quindi è un numero primo.

Al termine dell'elaborazione l'elenco contiene soltanto i numeri primi nell'intervallo da 1 a N.

$$ 1 \ , \ 2 \ , \ 3 \ , \ 5 \ , \ 7 \ , \ ... \ , \ N $$

Il metodo dei rettangoli per calcolare l'integrale definito

Il metodo dei rettangoli calcola l'integrale definito di una funzione.

Come funziona?

Considero la funzione in un intervallo definito (a,b).

Suddivido l'intervallo (a,b) in n segmenti più piccoli di uguale lunghezza.

Il risultato è una partizione dell'intervallo.

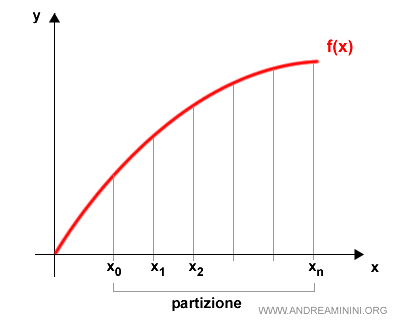
Per ciascun segmento della partizione calcolo l'altezza a partire da uno dei due estremi, ossia il segmento perpendicolare che unisce l'ascissa con il grafico della funzione.

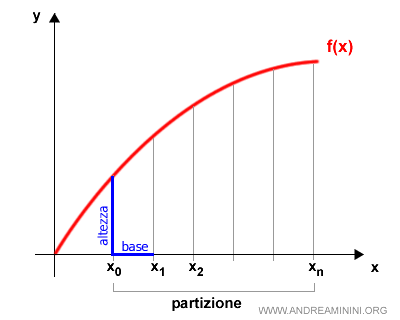
Poi moltiplico la lunghezza del segmento (base) per l'altezza e ottengo l'area del rettangolo.

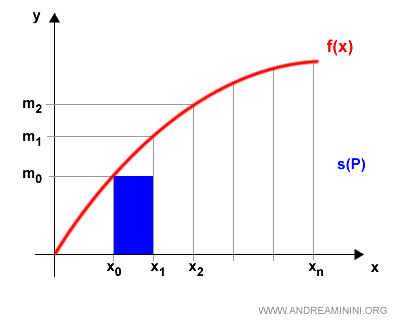
Infine passo ad analizzare il segmento successivo.

La somma delle aree di tutti i rettangoli approssima il valore dell'integrale definito della funzione nell'intervallo (a,b)

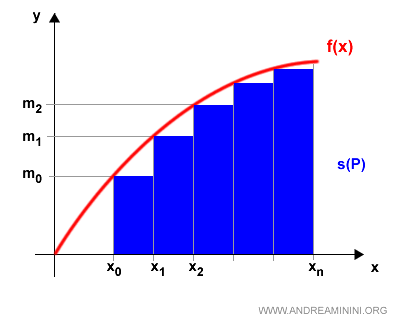
In questo caso è un'approssimazione per difetto perché ho tracciato l'altezza a partire dall'estremo di sinistra di ogni intervallo.

Nota. Tracciando l'altezza a partire dall'estremo di destra di ogni intervallo ottengo un'approssimazione per eccesso dell'integrale definito.

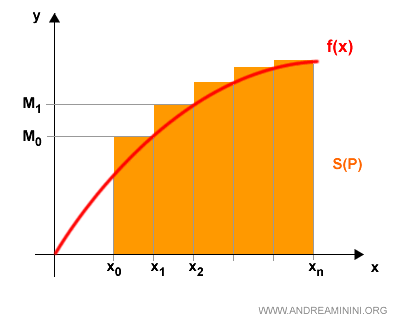
L'approssimazione dell'integrale definito è tanto più precisa, quanto più piccoli e numerosi sono i segmenti della partizione.

E così via.