Esercizio equazioni differenziali 31

Devo risolvere l'equazione differenziale del primo ordine.

$$ \begin{cases} y'= \frac{-t}{y} \\ \\ y(0)=5 \end{cases} $$

Si tratta di un problema di Cauchy

L'equazione differenziale è del tipo y'+a(t)b(y)=0 a variabili separabili con a(t)=1 e b(y)=1/y

Riscrivo y' nella notazione dy/dt

$$ \frac{dy}{dt} = \frac{-t}{y} $$

Separaro le variabili

$$ y \ dy = -t \ dt $$

Integro entrambi i membri per le rispettive variabili

$$ \int y \ dy = \int -t \ dt $$

$$ \int y \ dy = - \int t \ dt $$

$$ \frac{y^2}{2} +c_1 = - \frac{t^2}{2} +c_2 $$

Moltiplico entrambi i membri per due

$$ 2 \cdot (\frac{y^2}{2} +c_1) = 2 \cdot( - \frac{t^2}{2} +c_2) $$

$$ y^2 + \frac{c_1}{2} = - t^2 + \frac{c_2}{2} $$

Accorpo le due costanti in un'unica costante c=c₂/2-c₁/2

$$ y^2 = -t^2 +c $$

Ricavo la funzione incognita y

$$ \sqrt{y^2} = \sqrt{ -t^2 +c} $$

$$ y = \pm \sqrt{ c-t^2} $$

Scelgo il segno in base alla condizione iniziale y(0)=5 dove t=0

$$ 5 = \pm \sqrt{ c-0} $$

$$ 5 = \pm \sqrt{ c} $$

Essendo y=5 in questo caso il segno del lato destro è +

$$ 5 = + \sqrt{ c} $$

Quindi, la soluzione generale dell'equazione differenziale è

$$ y = + \sqrt{ c-t^2} $$

Ricavo la y e risolvo il problema di Cauchy applicando le condizioni iniziali y(0)=5 e t=0

$$ 5 = + \sqrt{ c-0} $$

$$ (5)^2 = +( \sqrt{ c} )^2 $$

$$ c=25 $$

Pertanto la soluzione di Cauchy è

$$ y = + \sqrt{ 25-t^2} $$

Verifica. La derivata della soluzione generale è $$ y' = D_x[ \sqrt{ 25-t^2} ] $$ $$ y' = \frac{-x}{ \sqrt{ 25-t^2} } $$ $$ y' = \frac{-x}{y} $$ La verifica è soddisfatta.

Lo studio della soluzione

L'intervallo massimale di esistenza della soluzione è [-5,5]

Dove 5 è il tempo di vita nel futuro e -5 è il tempo di vita nel passato.

In questo caso nel futuro (t=5) si verifica un break down perché la soluzione esce dal compo di definizione del lato destro dell'equazione differenziale

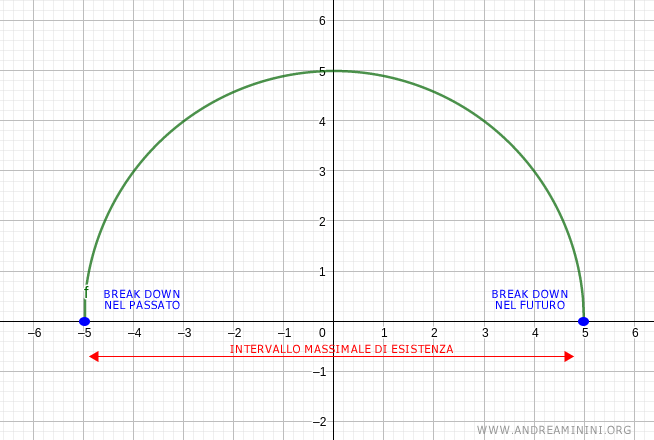
Nota. Il lato destro dell'equazione differenziale è -t/y. Quindi, in y=0 il lato destro dell'equazione non è definito. $$ y'= \frac{-t}{y} $$ Quando y=0 il lato destro è indefinito perché si verifica una divisione per 0 $$ y'= \frac{-t}{0} $$ Quindi, nel tempo di vita nel futuro (t=5) si presenta una morte del tipo break down.

Essendo una funzione pari la soluzione è in break-down anche nel passato (t=-5)

E così via