Istogramma
L'istogramma (o diagramma a barre) è un grafico che mostra come sono distribuiti dei dati usando delle barre.
- Se le barre hanno tutte la stessa larghezza, l'altezza di ciascuna rappresenta la frequenza dei dati in quell'intervallo. In questo caso si parla anche di ortogramma.
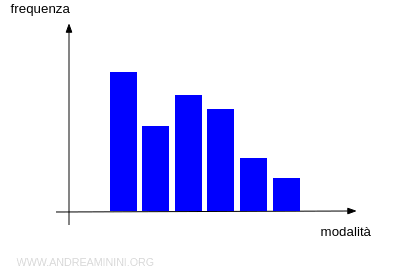
- Se le barre hanno larghezze diverse, è l'area della barra a indicare la frequenza, non l'altezza.
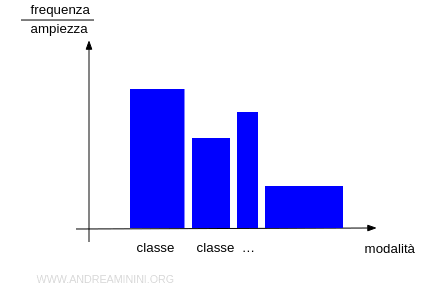
L'istogramma permette di visualizzare rapidamente e a colpo d'occhio come i dati sono distribuiti.
Ad esempio, se la maggior parte dei rettangoli è concentrata verso un lato del grafico, posso dedurre che i dati sono distribuiti asimmetricamente.
Esistono due tipi di istogrammi: con la base a larghezza fissa (ortogrammi) o variabile.
Ortogramma
Quando le barre dell'istogramma hanno le basi con la stessa larghezza, il grafico prende il nome di ortogramma.
In questo caso, l'altezza di ogni barra è direttamente proporzionale alla frequenza dei dati in quell'intervallo specifico.
Questo tipo di grafico è molto comune e facilita la lettura e l'interpretazione visiva della distribuzione dei dati.
Ad esempio, se la maggior parte dei rettangoli è concentrata verso un lato del grafico, posso dedurre che i dati sono distribuiti asimmetricamente. Se invece i rettangoli formano una curva simmetrica, questo potrebbe suggerire che i dati seguono una distribuzione normale.
Esempio
Considero il peso medio dei pacchi delle spedizioni di un e-commerce in un mese.
| Intervallo (kg) | Frequenza |
|---|---|
| 0 - 2 | 10 |
| 2 - 4 | 14 |
| 4 - 6 | 9 |
| 6 - 8 | 7 |
| 8 - 10 | 5 |
| Totale | 45 |
La prima colonna indica l'intervallo del peso delle spedizioni. Gli intervalli hanno la stessa ampiezza.
La seconda colonna indica la frequenza ossia il numero di spedizioni in ciascun intervallo di peso.
In questo caso l'altezza delle barre dell'istogramma è proporzionale alla frequenza di ciascuna classe, poiché tutte le classi hanno la stessa ampiezza.
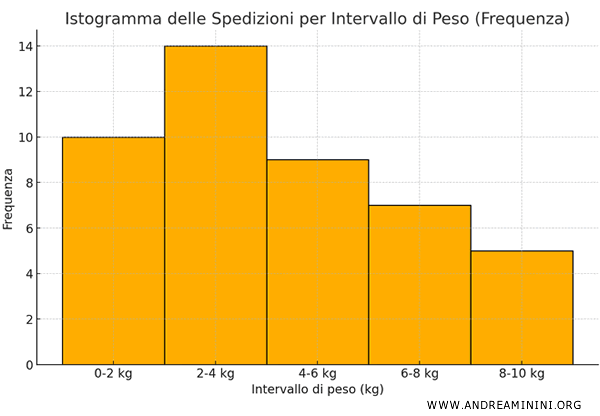
Come si può notare anche a colpo d'occhio, i rettangoli dell'istogramma hanno la base con la stessa larghezza.
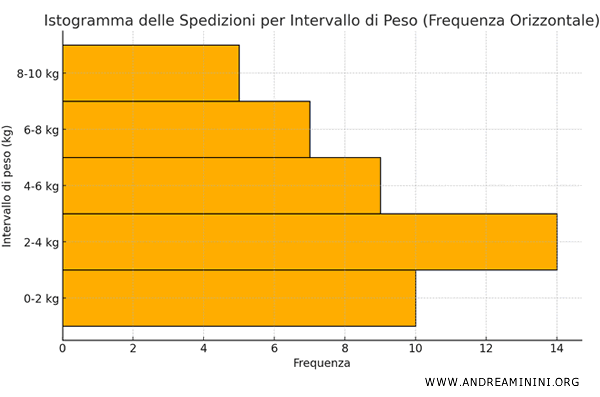
Nota. L'istogramma può essere rappresentato anche con la frequenza sull'asse orizzontale e le classi sull'asse verticale. In questo formato, le barre si estendono orizzontalmente, con la lunghezza proporzionale alla frequenza, anziché l'altezza. Nonostante la disposizione differente, tutte le barre mantengono la stessa larghezza verticale (base).
Istogramma con larghezze diverse
Quando le barre dell'istogramma hanno le basi con larghezze diverse, la frequenza di ogni modalità è proporzionale all'area della barra.
In questo caso, l'altezza delle barre non può essere utilizzata direttamente per confrontare le frequenze.
Per rendere il confronto significativo, è necessario considerare l'area totale di ogni barra, che risulta proporzionale alla frequenza dell'intervallo rappresentato.
Nota. Una barra bassa ma con la base molto larga potrebbe avere una frequenza più alta di una barra alta ma con base stretta o viceversa. In ogni caso l'altezza della barra non è più indicativa della frequenza.
Quando le larghezze delle barre sono diverse, l'altezza delle barre si calcola dividendo la frequenza per l'ampiezza dell'intervallo. Questo calcolo genera quella che è chiamata densità di frequenza.
$$ \text{Densità di frequenza} = \frac{\text{Frequenza}}{\text{Ampiezza dell'intervallo}} $$
In pratica, la densità di frequenza è il valore che viene rappresentato dall'altezza della barra, e assicura che l'area di ciascuna barra rimanga proporzionale alla frequenza.
Esempio
Considero il peso medio dei pacchi delle spedizioni di un e-commerce in un mese.
| Intervallo (kg) | Frequenza |
|---|---|
| 0 - 2 | 10 |
| 2 - 5 | 18 |
| 5 - 6 | 5 |
| 6 - 10 | 12 |
| Totale | 45 |
La prima colonna indica l'intervallo del peso delle spedizioni. Gli intervalli hanno ampiezze diverse.
La seconda colonna (frequenza) indica il numero di spedizioni che rientrano in ciascun intervallo di peso.
In questo caso le classi hanno larghezze diverse. Quindi, per costruire l'istogramma devo prima calcolare la densità di frequenza di ogni classe.
Ad esempio, per l'intervallo 0-2 kg ha un'ampiezza delll'intervallo pari a 2 e come frequenza 10. Quindi, la densità di frequenza è 5.
$$ \text{Densità di frequenza} = \frac{\text{Frequenza}}{\text{Ampiezza dell'intervallo}} = \frac{10}{2} = 5 $$
Per l'intervallo 2-5 kg la densità di frequenza è 6.
$$ \text{Densità di frequenza} = \frac{18}{3} = 6 $$
Per l'intervallo 5-6 kg la densità di frequenza è 5.
$$ \text{Densità di frequenza} = \frac{5}{1} = 5 $$
Per l'intervallo 6-10 kg la densità di frequenza è 3.
$$ \text{Densità di frequenza} = \frac{12}{4} = 3 $$
Aggiungo un'ulteriore colonna alla tabella per rappresentare anche la densità di frequenza.
| Intervallo (kg) | Frequenza | Densità di frequenza |
|---|---|---|
| 0 - 2 | 10 | 5 |
| 2 - 5 | 18 | 6 |
| 5 - 6 | 5 | 5 |
| 6 - 10 | 12 | 3 |
| Totale | 45 |
Infine, disegno l'istogramma misurando sull'asse verticale la densità di frequenza per ciascuna classe.
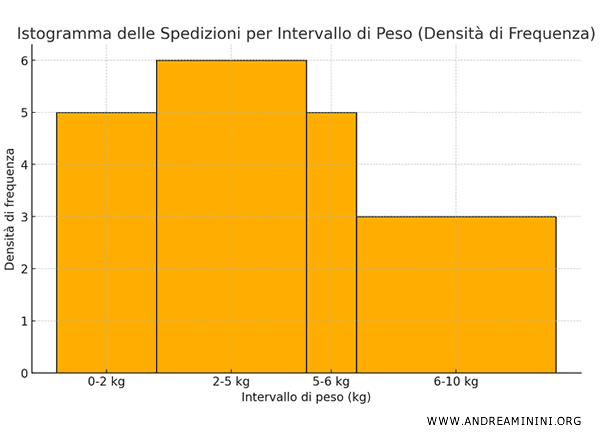
In questo mofo, anche se le ampiezze degli intervalli sono diverse, l'area di ogni barra rappresenta correttamente la frequenza dei dati grazie al calcolo della densità di frequenza.
Ad esempio, l'area della prima barra è 2×5=10 ed è uguale alla frequenza della classe 0-2 kg. L'area della prima barra è 3×6=18 ed è uguale alla frequenza della classe 2-5 kg. E via dicendo.
Questo è fondamentale per mantenere una rappresentazione accurata e coerente della distribuzione dei dati.
Nota. Se considerassi la frequenza delle classi anziché la densità di frequenza, la classe 6-10 kg apparirebbe più alta delle classi 0-2 kg e 5-6 kg distorcendo l'interpretazione grafica dei dati.
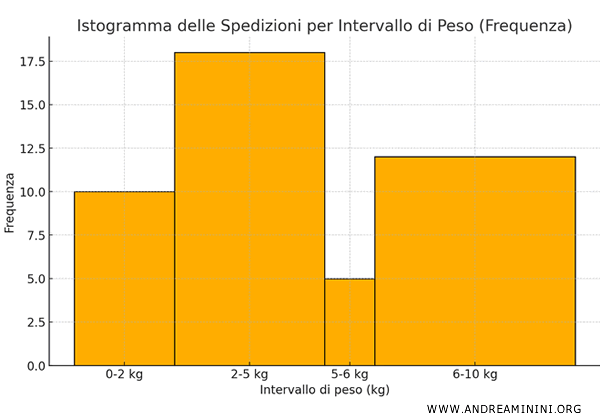
E così via.
