Covarianza
La covarianza è una misura statistica che descrive il grado di variazione simultanea tra due variabili $ X $ e $ Y $. Per \(n\) coppie di dati \((X_i, Y_i)\), la covarianza \( \text{Cov}(X, Y) \) è calcolata come: $$ \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})(Y_i - \overline{Y}) $$ Dove \( \overline{X} \) e \( \overline{Y} \) sono le medie delle variabili \( X \) e \( Y \).
La covarianza restituisce un valore assoluto che indica la relazione lineare tra le due variabili:
- Se la covarianza è positiva, significa che, in media, quando una delle variabili aumenta, anche l’altra tende ad aumentare.
- Se la covarianza è negativa, indica che, quando una delle variabili aumenta, l’altra tende a diminuire.
Infine, una covarianza di zero indica che non vi è alcuna relazione lineare tra le due variabili, ma questo non implica necessariamente indipendenza.
Relazione tra covarianza e correlazione. La covarianza misura la relazione in termini assoluti tra due variabili, fornisce solo informazioni su come due variabili si muovono insieme, ma dipende dalle unità di misura delle variabili e non dice nulla sull'intensità, né posso usarla per fare confronti. La correlazione va oltre, indica sia la forza che la direzione della relazione delle variabili statistiche. Ad esempio, la covarianza è utilizzata nel coefficiente di Pearson per misurare la correlazione su una scala tra -1 e 1. Quindi, la correlazione è una versione normalizzata della covarianza.
Un esempio pratico
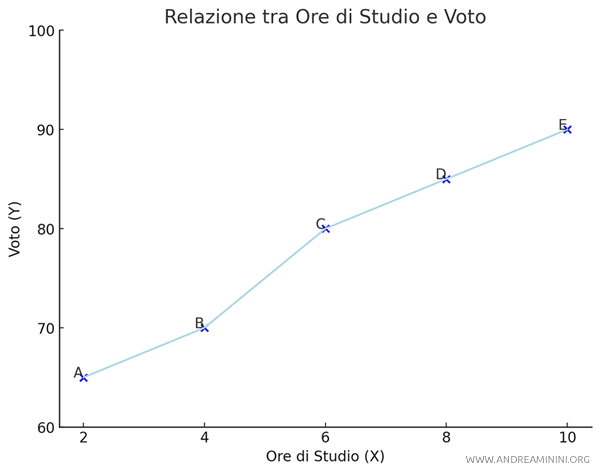
Devo calcolare la covarianza tra due variabili: il numero di ore di studio ( X ) e i voti di un gruppo di studenti ( Y ).
| Studente | Ore di studio (X) | Voto (Y) |
|---|---|---|
| A | 2 | 65 |
| B | 4 | 70 |
| C | 6 | 80 |
| D | 8 | 85 |
| E | 10 | 90 |
Per prima cosa calcolo le medie di \( X \) e \( Y \)
$$ \overline{X} = \frac{2 + 4 + 6 + 8 + 10}{5} = 6 $$
$$ \overline{Y} = \frac{65 + 70 + 80 + 85 + 90}{5} = 78 $$
Una volta note le medie, posso calcolare la covarianza tra X e Y
$$ \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})(Y_i - \overline{Y}) $$
$$ \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - 6)(Y_i - 78) $$
Poi calcoliamo i prodotti delle differenze rispetto alle medie
Facendo i calcoli per ciascun elemento della sommatoria:
- Studente A: \((2 - 6)(65 - 78) = (-4)(-13) = 52\)
- Studente B: \((4 - 6)(70 - 78) = (-2)(-8) = 16\)
- Studente C: \((6 - 6)(80 - 78) = (0)(2) = 0\)
- Studente D: \((8 - 6)(85 - 78) = (2)(7) = 14\)
- Studente E: \((10 - 6)(90 - 78) = (4)(12) = 48\)
Quindi la covarianza è la seguente:
$$ \text{Cov}(X, Y) = \frac{52 + 16 + 0 + 14 + 48}{5} $$
$$ \text{Cov}(X, Y) = \frac{130}{5} $$
$$ \text{Cov}(X, Y) = 26 $$
In questo caso, la covarianza tra le ore di studio e i voti è 26.
Si tratta di un valore assoluto positivo. Questo indica una relazione positiva tra le due variabili.
In altre parole, quando aumentano le ore di studio, aumentano anche i voti.
Una formula alternativa per calcolare la covarianza
Per calcolare la covarianza si può usare anche questa formula $$ \text{cov}(X, Y) = \frac{ \sum x_i y_i }{n} - \bar{x} \bar{y} $$ oppure $$\text{cov}(X, Y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$ Dove \( \overline{x} \) e \( \overline{y} \) sono le medie aritmetiche delle variabili: $ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i $ e $ \bar{y} = \frac{1}{n} \sum_{i=1}^n y_i $
Vediamo come si arriva a quella forma della covarianza.
Parto dalla definizione classica:
$$ \text{cov}(X, Y) = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) $$
Sviluppo l’espressione espandendo il prodotto $(x_i - \bar{x})(y_i - \bar{y}) = x_i y_i - x_i \bar{y} - \bar{x} y_i + \bar{x} \bar{y} $
$$ \text{cov}(X, Y) = \frac{1}{n} \sum_{i=1}^n x_i y_i - x_i \bar{y} - \bar{x} y_i + \bar{x} \bar{y} $$
Separo i termini:
$$ \text{cov}(X, Y) = \frac{1}{n} ( \sum_{i=1}^n x_i y_i - \bar{y} \sum_{i=1}^n x_i - \bar{x} \sum_{i=1}^n y_i + n \bar{x} \bar{y} ) $$
Sapendo che $ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i $ sostituisco $ \sum_{i=1}^n x_i = n \bar{x} $
$$ \text{cov}(X, Y) = \frac{1}{n} ( \sum_{i=1}^n x_i y_i - \bar{y} ( n \bar{x} ) - \bar{x} \sum_{i=1}^n y_i + n \bar{x} \bar{y} ) $$
Sapendo che $ \bar{y} = \frac{1}{n} \sum_{i=1}^n y_i $ sostituisco $ \sum_{i=1}^n y_i = n \bar{y} $
$$ \text{cov}(X, Y) = \frac{1}{n} ( \sum_{i=1}^n x_i y_i - \bar{y} n \bar{x} - \bar{x} ( n \bar{y} ) + n \bar{x} \bar{y} ) $$
Quindi ottengo:
$$ \text{cov}(X, Y) = \frac{1}{n} ( \sum_{i=1}^n x_i y_i - \bar{y} n \bar{x} - \bar{x} n \bar{y} + n \bar{x} \bar{y} ) $$
$$ \require{cancel} \text{cov}(X, Y) = \frac{1}{n} ( \sum_{i=1}^n x_i y_i - n \bar{x} \bar{y} - \cancel{ n \bar{x} \bar{y} } + \cancel{ n \bar{x} \bar{y} ) } $$
$$ \text{cov}(X, Y) = \frac{1}{n} \left( \sum_{i=1}^n x_i y_i - n \bar{x} \bar{y} \right) $$
Che può anche essere scritta così:
$$ \text{cov}(X, Y) = \frac{ \sum x_i y_i }{n} - \bar{x} \bar{y} $$
Forma equivalente. Per ottenere la seconda forma svolgo ancora qualche passaggio. Ho trovato questa forma della covarianza: $$ \text{cov}(X, Y) = \frac{ \sum x_i y_i }{n} - \bar{x} \bar{y} $$ Ora, ricodando che $ \bar{x} = \frac{ \sum x_i }{n} $ e $\bar{y} = \frac{ \sum y_i }{n} $ sostituisco $ \bar{x} \bar{y} = \left( \frac{ \sum x_i }{n} \right) \left( \frac{ \sum y_i }{n} \right) = \frac{ \sum x_i \cdot \sum y_i }{n^2 } $ $$ \text{cov}(X, Y) = \frac{ \sum x_i y_i }{n} - \frac{ \sum x_i \cdot \sum y_i }{n^2 } $$ $$\text{cov}(X, Y) = \frac{1}{n} \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n^2} $$ $$\text{cov}(X, Y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$
Perché si usa la forma equivalente?
La forma equivalente della covarianza è molto più comoda nei calcoli a mano perché mi evita di dover calcolare le medie aritmetiche.
$$\text{cov}(X, Y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$
Inoltre, spesso ho già le somme $ \sum x_i $, $ \sum y_i $ già disponibili nella tabella dei dati.
Esempio
Riprendo lo stesso esempio fatto in precedenza, dove devo calcolare la covarianza tra due variabili: il numero di ore di studio ( X ) e i voti di un gruppo di studenti ( Y ).
| Studente | Ore di studio (X) | Voto (Y) |
|---|---|---|
| A | 2 | 65 |
| B | 4 | 70 |
| C | 6 | 80 |
| D | 8 | 85 |
| E | 10 | 90 |
Nella tabella ci sono $n = 5 $ elementi.
Calcolo le somme delle variabili e del loro prodotto
$$ \sum x_i = 2 + 4 + 6 + 8 + 10 = 30 $$
$$ \sum y_i = 65 + 70 + 80 + 85 + 90 = 390 $$
$$\sum x\_i y\_i = 130 + 280 + 480 + 680 + 900 = 2470 $$
Sostituisco i dati nella formula
$$ \text{cov}(X, Y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$
$$ \text{cov}(X, Y) = \frac{1}{5} \left( 2470 - \frac{30 \cdot 390}{5} \right) $$
$$ \text{cov}(X, Y) = \frac{1}{5} \left( 2470 - \frac{11700}{5} \right) $$
$$ \text{cov}(X, Y) = \frac{1}{5} \left( 2470 - 2340 \right) $$
$$\text{cov}(X, Y) = \frac{1}{5} (130) $$
$$\text{cov}(X, Y) = 26 $$
La covarianza tra ore di studio e voto è 26.
Sono giunto allo stesso risultato dell'esempio precedente senza aver calcolato le medie aritmetiche delle variabili.
Poiché è positiva, indica che all’aumentare delle ore di studio tendenzialmente aumenta anche il voto.
Nota. In alternativa, avrei potuto usare la formula con le medie aritmetiche, giungendo comunque allo stesso risultato $$ \text{cov}(X, Y) = \frac{ \sum x_i y_i }{n} - \bar{x} \bar{y} $$ oppure $$\text{cov}(X, Y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$ In questo caso però, oltre a $ n=5 $ e alle somme $ \sum x_i = 30 $, $ \sum y_i = 390 $ e $ \sum x_i y_i = 2470 $, devo conoscere anche le medie $ \bar{x} = \frac{ \sum x_i }{n } = \frac{30}{5} = 6 $ e $ \bar{y} = \frac{ \sum y_i }{n } = \frac{390}{5} = 78 $ $$ \text{cov}(X, Y) = \frac{ 2470 }{5} - 6 \cdot 78 $$ $$ \text{cov}(X, Y) = 494 - 468 $$ $$ \text{cov}(X, Y) = 26 $$ Il risultato finale è lo stesso. Quindi, la scelta tra l'una e l'altra dipende da quali dati ho già disponibili e da quale mi fa risparmiare più calcoli.
La covarianza nulla non implica indipendenza
La covarianza misura solo la relazione lineare tra due variabili.
Se la covarianza è zero, significa che non c’è una relazione lineare tra le variabili, ma potrebbero comunque esistere altre forme di dipendenza non lineare.
In altre parole, due variabili possono essere correlate in modo complesso, ad esempio secondo una relazione quadratica o esponenziale, e questo tipo di dipendenza non sarebbe rilevato dalla covarianza.
Esempio. Un esempio classico è quello di due variabili \( X \) e \( Y = X^2 \), dove \( X \) è una variabile centrata rispetto alla sua media (cioè, ha media zero). In questo caso, \( X \) e \( Y \) sono dipendenti perché la conoscenza di \( X \) mi permette di determinare \( Y \)), ma la loro covarianza è zero perché la relazione non è lineare.
La differenza tra covarianza e correlazione
La covarianza e la correlazione non sono esattamente la stessa cosa
- La covarianza misura la relazione in termini assoluti e dipende dalle unità di misura delle variabili.
- La correlazione misura la relazione in termini relativi ed è un valore standardizzato che mi permette di fare anche confronti diretti.
Quindi, mentre la covarianza fornisce informazioni su come due variabili si muovono insieme in termini assoluti, la correlazione standardizza questo movimento, rendendo possibile un confronto indipendentemente dalle unità di misura delle variabili.
Come si misura la correlazione?
La covarianza fornisce alcune informazioni ma non è molto utile come indicatore della correlazione.
Per misurare la correlazione devo utilizzare altri strumenti statistici come il coefficiente di Person.
Ad esempio, nel coefficiente di Pearson la formula della correlazione \( \rho(X, Y) \) tra due variabili \( X \) e \( Y \) è data da:
$$ \rho(X, Y) = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} $$
Dove \( \text{Cov}(X, Y) \) è la covarianza tra \( X \) e \( Y \), mentre \( \sigma_X \) e \( \sigma_Y \) sono le deviazioni standard di \( X \) e \( Y \).
A differenza della covarianza, il coefficiente di Pearson varia tra -1 e 1.
- \( \rho(X, Y) = 1 \): indica una correlazione perfettamente positiva; le variabili si muovono insieme in modo proporzionale.
- \( \rho(X, Y) = -1 \): indica una correlazione perfettamente negativa; le variabili si muovono in direzioni opposte in modo proporzionale.
- \( \rho(X, Y) = 0 \): indica assenza di relazione lineare (ma non esclude dipendenze non lineari).
Poiché è una misura normalizzata, la correlazione è invariante rispetto a trasformazioni di scala sulle variabili, come moltiplicazioni e traslazioni.
Inoltre, è particolarmente utile per confrontare relazioni tra variabili con unità di misura diverse.
Note
Alcune note personali e osservazioni aggiunte sulla covarianza
- La formula operativa della covarianza si riduce a quella della varianza quando $ x=y $
Considero la formula operativa della covarianza : $$ \text{Cov}(x,y) = \frac{1}{n} \left( \sum x_i y_i - \frac{ \sum x_i \cdot \sum y_i }{n} \right) $$ Quando $x = y $, questa coincide con la varianza: $$ \text{Var}(x) = \frac{1}{n} \left( \sum x_i^2 - \frac{ ( \sum x_i )^2 }{n} \right ) $$ Quindi, questa formula operativa mi permette di calcolare sia la varianza che la covarianza in modo più pratico, senza dover prima calcolare la media e poi gli scarti. È molto utile nei programmi statistici o nei calcoli a mano perché richiede meno passaggi.
E così via.
