Interpolazione
L'interpolazione è una tecnica matematica che permette di stimare valori sconosciuti all'interno di un intervallo basandosi su dati noti.
In pratica, cerco una funzione (detta funzione interpolante) che passa attraverso o vicino a un insieme di punti dati noti (detti punti o nodi di interpolazione) e la utilizzo per prevedere o stimare i valori degli altri punti nell'intervallo.
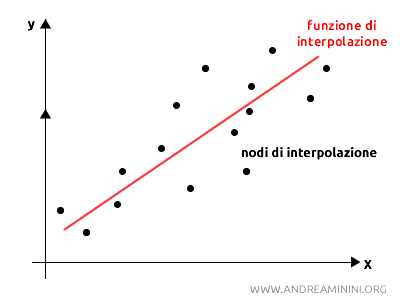
Questa tecnica mi consente di ottenere una rappresentazione continua di un fenomeno all'interno di un intervallo, partendo da un insieme limitato di dati.
In altre parole, l'interpolazione "riempie i vuoti" tra i dati noti e mi permettei di prevedere come si comporterebbe il fenomeno tra i punti osservati.
Esempio. Se conosco solo alcuni punti di riferimento in un intervallo (a,b), l'interpolazione mi consente di costruire una funzione continua che li collega. Una volta definita la funzione interpolante, posso utilizzarla per stimare i valori anche nei punti per cui non ho dati diretti
Esistono due tipi principali di funzioni interpolanti: l'interpolazione matematica e l'interpolazione statistica, ognuna con caratteristiche e scopi distinti.
- Interpolazione matematica: La funzione interpolante passa esattamente per i punti dati, utile quando i dati sono precisi.
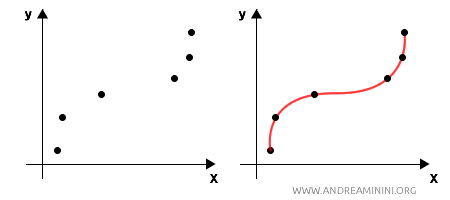
- Interpolazione statistica: La funzione interpolante si avvicina ai punti dati, minimizzando gli errori, utile quando i dati sono soggetti a errori o rumore.
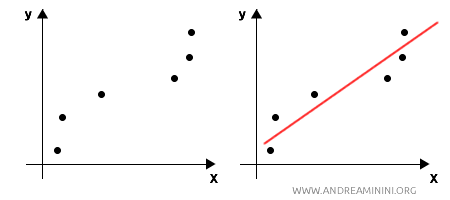
L'interpolazione statistica è ampiamente utilizzata in statistica e scienze applicate, mentre l'interpolazione matematica è più comune in contesti teorici o quando i dati sono considerati esatti.
Interpolazione matematica
Nell'interpolazione matematica, l'obiettivo è trovare una funzione interpolante che passi esattamente per tutti i punti noti o dati sperimentali.
In altre parole, la funzione interpolante restituisce esattamente i valori dei punti noti.
Questo tipo di interpolazione viene utilizzato quando i dati sono considerati accurati e privi di errori significativi, o quando si ha bisogno di una rappresentazione esatta del fenomeno descritto dai dati.
Esempio
Considero alcuni punti di interpolazione sul piano cartesiano.
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Se rappresento i punti sul piano ottengo un diagramma a dispersione (o nuvole di punti) in cui i punti sono scollegati tra loro.
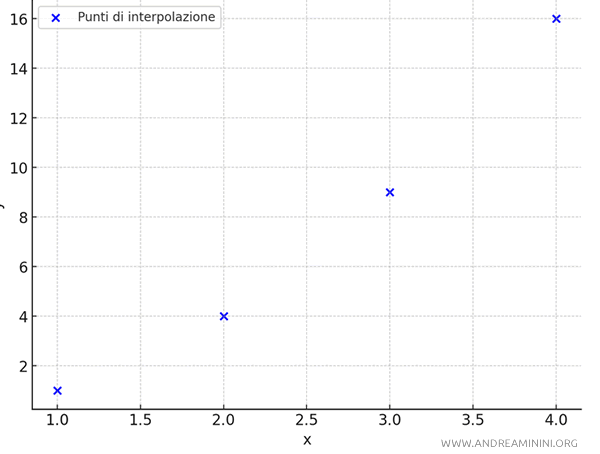
La funzione polinomiale che passa esattamente per questi punti è:
$$ y = x^2 $$
Questo polinomio è una rappresentazione perfetta dei punti dati forniti, che segue la legge \(y = x^2\).
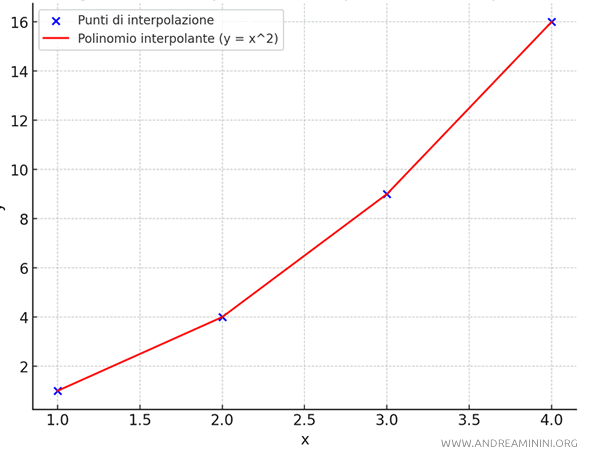
Nota. Il polinomio \(y = x^2\) l'ho ottenuto applicando il metodo di interpolazione di Lagrange. In questo caso è stato facile trovare la funzione interpolante. Va però detto che non è sempre così. Al contrario, spesso è difficile trovare una funzione matematica che passi esattamente per tutti i punti noti. Pertanto, si ricorre all'interpolazione statistica.
Interpolazione statistica
Nell''interpolazione statistica si cerca una funzione che si avvicini ai punti noti quanto più possibile, minimizzando gli errori globali tra i valori osservati e quelli stimati dalla funzione interpolante.
In questo caso, la funzione interpolante non deve necessariamente passare esattamente per ogni punto, ma piuttosto "avvicinarsi" ai punti dati.
È la tecnica più adatta per interpretare dati con rumore o incertezze, come quelli provenienti da rilevazioni sperimentali.
Esempio
Considero gli stessi dati dell'esempio precedente.
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
In questo caso, però, voglio trovare una funzione che si avvicina ai punti dati quanto più possibile tramite l'interpolazione statistica.
La funzione interpolante non deve necessariamente passare per i punti noti.

Per farlo utilizzo una tecnica di interpolazione statistica detta regressione lineare e individuo una retta $ y = 5x-5 $ che approssima i punti (vedi "come si calcola la retta interpolante").
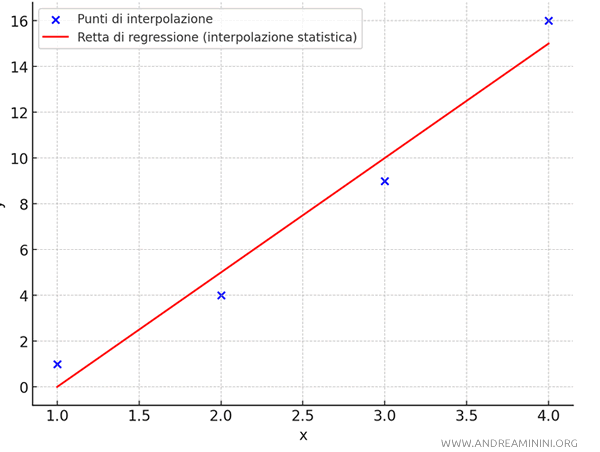
Come si può notare, la retta non passa esattamente per tutti i punti, ma cerca di avvicinarsi a essi minimizzando gli errori complessivi. E' un classico esempio di interpolazione statistica.
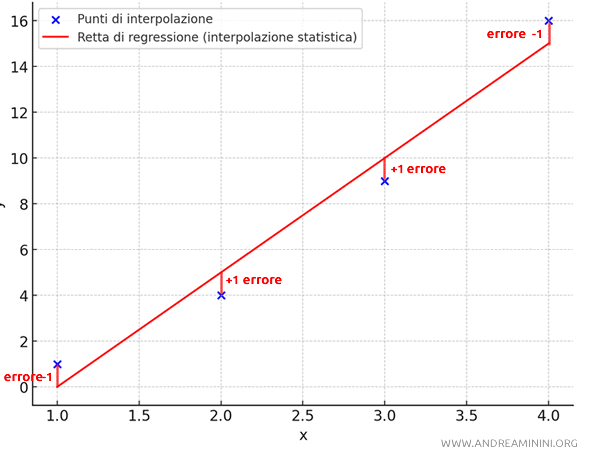
La differenza tra un punto noto \( y_i \) e un valore stimato dalla retta di regressione \( \hat{y}_i \) è detto errore parziale di accostamento.
$$ e_i = y_i - \hat{y_i} $$
Dove \( y_i \) sono i valori reali (i punti dati noti), mentre \( \hat{y}_i \) sono i valori stimati dalla retta di regressione.
| x | y | Valori stimati ( $ \hat{y} $ ) | Errore $ e_i = y - \hat{y} $ |
|---|---|---|---|
| 1 | 1 | 0.0 | 1.0 |
| 2 | 4 | 5.0 | -1.0 |
| 3 | 9 | 10.0 | -1.0 |
| 4 | 16 | 15.0 | 1.0 |
La somma degli errori parziali misura l'errore totale di approssimazione dovuto all'interpolazione.
$$ e = \sum_{i=1}^{n} e_i = \sum_{i=1}^{n} y_i - \hat{y_i} $$
Quest'ultimo però non è un buon indicatore dell'errore totale perché ,come in questo esempio, può accadere che gli errori parziali positivi e negativi si compensino tra loro.
$$ e= \sum_{i=1}^{n} y_i - \hat{y}_i = (1-0)+(4-5)+(9-10)+(16-15) $$
$$ e= \sum_{i=1}^{n} y_i - \hat{y}_i = 1-1-1+1 $$
$$ e= \sum_{i=1}^{n} y_i - \hat{y}_i = 0$$
Per evitare questo problema, è preferibile calcolare l'errore totale utilizzando la somma dei quadrati degli errori parziali (S).
$$ S = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Questo evita la compensazione tra gli errori parziali positivi e negativi.
In questo esempio la somma dei quadrati degli errori (S) è pari a 4.0.
$$ S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = (1-0)^2+(4-5)^2+(9-10)^2+(16-15)^2 $$
$$ S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = (1)^2+(-1)^2+(-1)^2+(1)^2 $$
$$ S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = 1+1+1+1 $$
$$ S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = 4 $$
Questo valore rappresenta l'errore totale di approssimazione tra i punti noti e i valori stimati dalla retta di regressione.
E così via.
