Chi-quadro

Il chi-quadro o chi-quadrato (χ²) è un test statistico utilizzato per determinare se c'è una differenza significativa tra le frequenze osservate e le frequenze attese in una o più categorie.

Il test del chi-quadro si utilizza principalmente in due situazioni:

• Test di indipendenza: Serve per verificare se due variabili categoriali sono indipendenti. Ad esempio, lo potrei usare per capire se c'è una relazione tra il genere (maschio/femmina) e la preferenza per un tipo di prodotto (A/B).
• Test di adattamento: Serve per confrontare le frequenze osservate con quelle attese in base a una distribuzione teorica. Ad esempio, posso usarlo per verificare se i risultati del lancio di un dado sono equamente distribuiti.

In generale, è uno strumento molto utile per verificare se due variabili categoriali sono indipendenti o per confrontare la distribuzione osservata con una distribuzione teorica.

Nota. Il chi-quadro (o chi-quadrato) è conosciuto anche come indice di Pearson dal nome dello statistico Karl Pearson, che ha sviluppato il test per analizzare la relazione tra variabili. A volte come indice di Pizzetti-Pearson, perché in alcune fonti viene attribuito anche al contributo di Paolo Pizzetti, un altro statistico. Quando viene usato specificamente per verificare se due variabili categoriali sono indipendenti è spesso indicato semplicemente come Test di indipendenza.

Come si calcola il chi-quadro

Il chi-quadro si calcola con la seguente formula:

$$ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} $$

Dove:

• \( O_i \) sono le frequenze assolute osservate nelle categorie.
• \( E_i \) sono le frequenze attese in base all'ipotesi nulla che di solito è l'indipendenza delle variabili o una distribuzione teorica specifica.

Se il valore di \( \chi^2 \) è grande, vuole dire che c'è una discrepanza significativa tra le frequenze osservate e quelle attese.

Come si interpreta il valore del Chi-quadrato?

Per interpretare il risultato del test, confronto il valore calcolato di \( \chi^2 \) con un valore critico \( \chi^2_{\alpha, df} \) tratto dalla distribuzione del chi-quadro.

• Se \( \chi^2 \) calcolato è maggiore del valore critico, le variabili sono dipendenti oppure la distribuzione osservata non segue quella teorica. L'ipotesi nulla (indipendenza) viene rifiutata.
• Se \( \chi^2 \) calcolato è minore del valore critico, le variabili potrebbero essere indipendenti, perché non ci sono prove sufficienti per affermare che le variabili sono associate tra loro (dipendenti) o che la distribuzione differisce da quella attesa. In questo caso l'ipotesi nulla non può essere scartata.

Il valore critico si indica comunemente con \( \chi^2_{\alpha, df} \), dove:

• \( \alpha \) rappresenta il livello di significatività (ad esempio, 0,05 o 0,01). E' una misura che stabilisce il criterio di decisione per accettare o rifiutare un’ipotesi, in base alla probabilità di errore che sono disposto a tollerare.

  Ad esempio, un livello di significatività comune è α=0,05 significa che c'è un 5% di probabilità di commettere un errore di tipo I. In altre parole, accetto il rischio che il risultato sia dovuto al caso 1 volta su 20.

• \( df \) rappresenta i gradi di libertà del test. I gradi di libertà sono calcolati in base alle dimensioni della tabella a doppia entrata (o tabella di contingenza) usata per analizzare i dati. $$ df = (r - 1) \times (c - 1) $$ Dove $ r $ è il numero di righe della tabella e $ c $ è il numero di colonne. In altre parole, il grado di libertà riflette le combinazioni possibili tra le varie categorie delle due variabili all'interno della tabella di contingenza.
  

  Ad esempio, in una tabella a doppia entrata con r=2 righe e c=3 colonne il grado di libertà è df=2. $$ df = (2 - 1) \times (3 - 1) = 2 $$

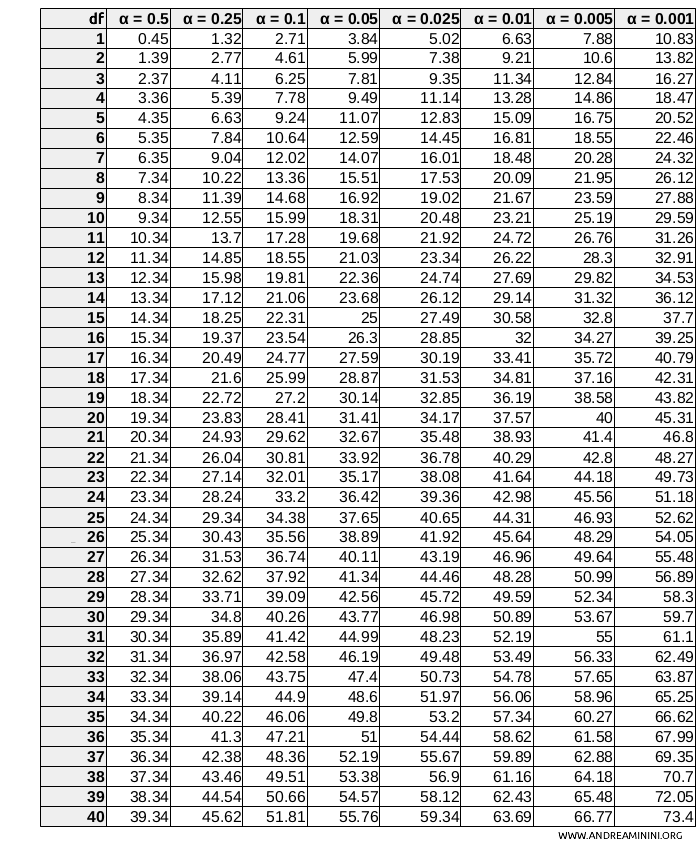
Per trovare il valore critico devo consultare la tabella della distribuzione del chi-quadro.

Ad esempio, \( \chi^2_{0.05, 2}  \) indica il valore critico per un livello di significatività del 5% (ovvero α=0.05) e df=2 gradi di libertà. Si trova guardando il valore corrispondente alla riga $ df=2 $ e alla colonna $ \alpha=0.05 $. In questo caso il valore critico è \( \chi^2_{0.05, 2}  = 5.99 \)

Un esempio pratico

Voglio verificare se c'è una relazione tra il genere (Maschio/Femmina) e la preferenza per un tipo di snack (A, B, o C).

Ho fatto un sondaggio su 100 persone raccogliendo i seguenti dati:

	Snack A	Snack B	Snack C	Totale
Maschio	20	15	10	45
Femmina	10	25	20	55
Totale	30	40	30	100

Nella tabella a doppia entrata sono indicate le frequenze assolute, ovvero quante persone hanno mostrato una preferenza per uno snack e il genere della persona.

La tabella è composta da $ r=2 $ righe e $ c=3 $ colonne, togliendo quelle relative ai totali parziali.

Nota. La tabella a doppia entrata utilizzata nel test del chi-quadro è anche chiamata tabella di contingenza o tabella delle contingenze. Dove per "contingenza" si intende la relazione o dipendenza tra due o più variabili. In pratica, una contingenza indica che l’occorrenza di una variabile può essere influenzata o associata all’occorrenza di un’altra variabile. Questa tabella mostra le frequenze congiunte delle categorie di due variabili e può includere sia le frequenze assolute osservate sia le frequenze attese.

Per prima cosa devo calcolare le frequenze attese (\( E_{ij} \)) usando la formula seguente:

$$ E_{ij} = \frac{(\text{Totale riga}) \times (\text{Totale colonna})}{\text{Totale generale}} $$

Le frequenze attese sono quelle frequenze che mi aspetterei di vedere quando le variabili sono indipendenti.

Calcolo le frequenze attese per ciascuna cella della tabella:

• Maschio, Snack A $$ E_{11} = \frac{(45) \times (30)}{100} = 13.5 $$
• Maschio, Snack B $$ E_{12} = \frac{(45) \times (40)}{100} = 18 $$
• Maschio, Snack C $$ E_{13} = \frac{(45) \times (30)}{100} = 13.5 $$
• Femmina, Snack A $$ E_{21} = \frac{(55) \times (30)}{100} = 16.5 $$
• Femmina, Snack B $$ E_{22} = \frac{(55) \times (40)}{100} = 22 $$
• Femmina, Snack C $$ E_{23} = \frac{(55) \times (30)}{100} = 16.5 $$

La tabella a doppia entrata con le frequenze attese diventa:

	Snack A	Snack B	Snack C	Totale
Maschio	13.5	18	13.5	45
Femmina	16.5	22	16.5	55
Totale	30	40	30	100

Una volta calcolate tutte le frequenze attese, posso applicare la formula del chi-quadro:

$$ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} $$

Dove \( O_{ij} \) sono le frequenze assolute osservate nel sondaggio e \( E_{ij} \) sono quelle attese.

Calcolo ogni termine della sommatoria:

• Maschio, Snack A $$ \frac{(20 - 13.5)^2}{13.5} = \frac{6.5^2}{13.5} \approx 3.13 $$
• Maschio, Snack B $$ \frac{(15 - 18)^2}{18} = \frac{(-3)^2}{18} \approx 0.5 $$
• Maschio, Snack C $$ \frac{(10 - 13.5)^2}{13.5} = \frac{(-3.5)^2}{13.5} \approx 0.91 $$
• Femmina, Snack A $$ \frac{(10 - 16.5)^2}{16.5} = \frac{(-6.5)^2}{16.5} \approx 2.56 $$
• Femmina, Snack B $$ \frac{(25 - 22)^2}{22} = \frac{3^2}{22} \approx 0.41 $$
• Femmina, Snack C $$ \frac{(20 - 16.5)^2}{16.5} = \frac{3.5^2}{16.5} \approx 0.74 $$

Poi sommo tutti i termini:

$$ \chi^2 = 3.13 + 0.5 + 0.91 + 2.56 + 0.41 + 0.74  $$

Il risultato finale è il valore del chi-quadro \( \chi^2 = 8.25 \).

$$ \chi^2 = 8.25 $$

Per interpretare il valore del chi-quadro, devo confrontarlo con un valore critico tratto dalla distribuzione del chi-quadro.

In questo caso la tabella a doppia entrata ha $ df=2 $ gradi di libertà perché è composta da due righe ( $ r=2 $) e tre colonne ( $ c=3 $ ).

$$ df = (r - 1) \times (c - 1) $$

$$ df = (2 - 1) \times (3 - 1) $$

$$ df = 2 $$

Scelgo come livello di significatività \( \alpha = 0.05 \) che equivale al 5% di probabilità che il risultato sia errato o dovuto al caso.

Guardando la tabella del chi-quadro ottengo il valore critico per $ df = 2 $ gradi di libertà e un livello di significatività  \( \alpha = 0.05 \) 

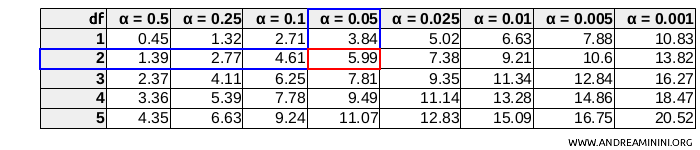
In questo caso il valore critico è circa 5.99.

$$ \chi^2_{0.05, 2}  = 5.99 $$

Infine, confronto il chi-quadro che ho calcolato sulla tabella $ \chi^2 = 8.25  $ con il valore critico $ \chi^2_{0.05, 2} = 5.99  $.

• Se $ \chi^2 >  \chi^2_{0.05, 2} $ le variabili sono dipendenti tra loro
• Se $ \chi^2 \le  \chi^2_{0.05, 2} $ le variabili potrebbero essere indipendenti tra loro

Poiché \( \chi^2 = 8.25 \) è maggiore di \( \chi^2_{0.05, 2} = 5.99 \) , deduco che le variabili non sono indipendenti e concludo che esiste una relazione significativa tra il genere (Maschio/Femmina) e la preferenza per lo snack (A,B o C).

Questo risultato mi suggerisce di scartare l'ipotesi nulla (indipendenza tra le due variabili).

In altre parole le due variabili statistiche sono dipendenti.

Nota. Viceversa, se il chi-quadro fosse stato minore o uguale al valore critico $ \chi^2 \le  \chi^2_{0.05, 2} $ , avrei accettato l'ipotesi nulla (indipendenza delle variabili), affermando che le preferenze per gli snack non dipendono dal genere.

Note a margine

Alcune note a margine e osservazioni sull'utilizzo del Chi-Quadro.

• Il Chi-quadro si applica solo ai dati disposti in categorie e non a dati quantitativi continui
  Il Chi-quadro si applica esclusivamente a dati categoriali (o qualitativi), cioè a dati che possono essere suddivisi in categorie distinte, come il genere (maschio/femmina), il colore degli occhi (chiaro/scuro), o la preferenza per un prodotto (A, B, C). Non è adatto per dati quantitativi continui, come altezze, pesi o temperature, che richiedono test statistici diversi, come il test t o l'ANOVA, che sono pensati per confrontare medie e varianze di dati numerici continui.

  Nota. Il motivo è che il Chi-quadro valuta la frequenza delle osservazioni in ciascuna categoria e confronta queste frequenze con quelle attese, quindi presuppone che i dati siano contati e non misurati su una scala continua.

• Le frequenze attese devono essere grandi
  Le frequenze attese in ciascuna categoria devono essere sufficientemente grandi (in genere almeno 5) per garantire che i risultati siano affidabili. Se le frequenze attese sono troppo piccole il calcolo del chi-quadro può diventare poco accurato e la distribuzione del chi-quadro potrebbe non approssimare correttamente i valori attesi, portando a conclusioni errate. Una regola pratica comunemente utilizzata è che le frequenze attese in ogni cella della tabella di contingenza dovrebbero essere almeno 5.
  

  Nota. Quando molte celle hanno frequenze attese inferiori a 5, una possibile soluzione è raggruppare le categorie per aumentare le frequenze attese in ogni cella. In alternativa, potrei utilizzare un test alternativo, come il test esatto di Fisher, che è più adatto quando le frequenze attese sono basse.

E così via.