Dipendenza e indipendenza statistica
In statistica, la dipendenza tra due caratteri o variabili si riferisce a una relazione in cui la variazione di una variabile influenza o è associata alla variazione di un’altra variabile.
Quando due caratteri sono dipendenti, le modalità di uno influenzano la distribuzione delle modalità dell'altro.
In altre parole, conoscere il valore o la categoria di una variabile mi fornisce informazioni utili per prevedere o spiegare il valore o la categoria dell’altra variabile.
Ad esempio, se sto osservando il genere (maschio o femmina) e il tipo di lettura preferita (romanzo, saggio, giallo) di un gruppo di persone, direi che c'è dipendenza se la preferenza di lettura cambia in modo significativo in base al genere della persona.
Se, invece, la distribuzione delle preferenze di lettura fosse uguale indipendentemente dal genere, si parla di indipendenza tra i due caratteri.
Per misurare e verificare la dipendenza o l'indipendenza tra due variabili, posso utilizzare test statistici come il test del \(\chi^2\) (chi quadrato).
Questo test confronta le frequenze osservate (quelle rilevate dai dati) con le frequenze teoriche che mi aspetterei in un caso di perfetta indipendenza.
Cosa sono le frequenze teoriche? Le frequenze teoriche sono i valori che ci aspettiamo di osservare se non ci fosse dipendenza tra le variabili in esame. Servono per confrontare i dati osservati e verificare se esiste una relazione significativa.
Un esempio pratico
In questo esempio considero un gruppo di 100 studenti e voglio verificare se c’è una dipendenza tra il genere (maschio o femmina) e la scelta di materia preferita (matematica o letteratura).
Raccolgo i dati e costruisco una tabella a doppia entrata.
| Matematica | Letteratura | Totale | |
|---|---|---|---|
| Maschi | 30 | 20 | 50 |
| Femmine | 10 | 40 | 50 |
| Totale | 40 | 60 | 100 |
In questa tabella ci sono le frequenze assolute dei dati raccolti.
Ora, per determinare se esiste una dipendenza tra il genere e la scelta della materia preferita, devo calcolare le frequenze teoriche ipotizzando che i due caratteri siano indipendenti.
Le frequenze teoriche si calcolano moltiplicando il totale della riga per il totale della colonna e dividendo il tutto per il totale generale:
- Matematica e maschi $$ \frac{50 \cdot 40}{100} = 20 $$
- Letteratura e maschi $$ \frac{50 \cdot 60}{100} = 30 $$
- Matematica e femmine $$ \frac{50 \cdot 40}{100} = 20 $$
- Letteratura e femmine $$ \frac{50 \cdot 60}{100} = 30 $$
Sostituisco le frequenze assolute (in rosso) con le frequenze teoriche nella tabella a doppia entrata.
| Matematica | Letteratura | Totale | |
|---|---|---|---|
| Maschi | 20 | 30 | 50 |
| Femmine | 20 | 30 | 50 |
| Totale | 40 | 60 | 100 |
A questo punto, confronto le frequenze osservate (tra parentesi) con quelle teoriche (in rosso) e noto già a colpo d'occhio che le frequenze osservate differiscono significativamente dalle frequenze teoriche.
| Matematica | Letteratura | Totale | |
|---|---|---|---|
| Maschi | 20 ( 30 ) | 30 (20) | 50 |
| Femmine | 20 ( 10 ) | 30 (40) | 50 |
| Totale | 40 | 60 | 100 |
Ad esempio, è evidente che i maschi preferiscono maggiormente la matematica rispetto a quanto previsto (30 vs 20). Le femmine, invece, preferiscono maggiormente la letteratura (40 vs 30).
Questa differenza suggerisce che esiste una dipendenza statistica tra il genere e la scelta della materia preferita. In altre parole, la preferenza per matematica o letteratura varia a seconda del genere.
Il test del chi quadrato
Per misurare statisticamente questa dipendenza, posso applicare il test del \(\chi^2\) (chi quadrato).
Se il risultato del test è significativo, conferma l'esistenza di una relazione tra i due caratteri, indicando che non sono indipendenti.
La formula per calcolare il valore del \(\chi^2\) è:
$$ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} $$
Dove \(O_{ij}\) sono le frequenze osservate, \(E_{ij}\) sono le frequenze teoriche calcolate in precedenza.
La differenza fra la frequenza assoluta e quella teorica $ O_{ij} - E_{ij} $ è detta contingenza.
Calcolo \(\chi^2\) per ogni cella:
- Matematica e maschi $$ \frac{(30 - 20)^2}{20} = \frac{100}{20} = 5 $$
- Letteratura e maschi $$ \frac{(20 - 30)^2}{30} = \frac{100}{30} \approx 3.33 $$
- Matematica e femmine $$ \frac{(10 - 20)^2}{20} = \frac{100}{20} = 5 $$
- Letteratura e femmine $$ \frac{(40 - 30)^2}{30} = \frac{100}{30} \approx 3.33 $$
Sommo tutti i risultati ottenuti:
$$ \chi^2 = 5 + 3.33 + 5 + 3.33 = 16.67 $$
Il valore del \(\chi^2\) è quindi \(16.67\).
Nota. Il valore \(\chi^2\) cresce con la quantità dei dati osservati. Per evitare questo problema spesso si utilizza il chi quadrato normalizzato. $$ C = \frac{\chi^2}{N \cdot (h-1)} $$ Dove $ N $ è il numero delle osservazioni, mentre $ h $ è il valore minore tra il numero di righe e di colonne della tabella. In questo caso $ N=100 $ poiché sono cento gli studenti intervistati e $ h=2 $, quindi il chi quadrato normalizzato è $$ C = \frac{16.67}{100 \cdot (2-1)} = \frac{16.67}{100} = 0.1667 $$ In alternativa, potrei calcolare l'indice quadratico medio di contingenza. $$ I_c = \sqrt{ \frac{ \chi^2 }{ \chi^2 + N } } = \sqrt{ \frac{16.67}{16.67+100} } = \sqrt{16.67}{116.67} = \sqrt{0.1427} =0.3778 $$
Infine, confronto questo valore con il valore critico della distribuzione \(\chi^2\) con 1 grado di libertà (dato da \((2-1) \times (2-1)\)) per determinare se c’è una dipendenza significativa tra le variabili.
Valore critico della distribuzione \(\chi^2\) e gradi di libertà
Quando si calcola il valore di \(\chi^2\), per determinare se è significativo, lo si confronta con un valore critico preso da una distribuzione \(\chi^2\).
Questo valore critico dipende:
- dal livello di significatività scelto (di solito \( \alpha = 0.05 \) che corrisponde a una probabilità del 5%)
- dai gradi di libertà del test.
I gradi di libertà (\(df\)) per una tabella di contingenza sono calcolati come:
$$ df = (\text{numero di righe} - 1) \times (\text{numero di colonne} - 1) $$
In questo esempio ci sono 2 righe (Maschi e Femmine) e 2 colonne (Matematica e Letteratura). Quindi:
$$ df = (2 - 1) \times (2 - 1) = 1 $$
Per \(df = 1\) e \( \alpha = 0.05 \), il valore critico è circa 3.841.
Nota. Il valore 3.841 lo ottengo dalla distribuzione chi quadrato ( \( \chi^2 \) ) corrispondente a un livello di significatività del 5% (o \( \alpha = 0.05 \) ) con 1 grado di libertà. Esistono delle tabelle standard della distribuzione \(\chi^2\) che mostrano i valori critici per diversi gradi di libertà e livelli di significatività.
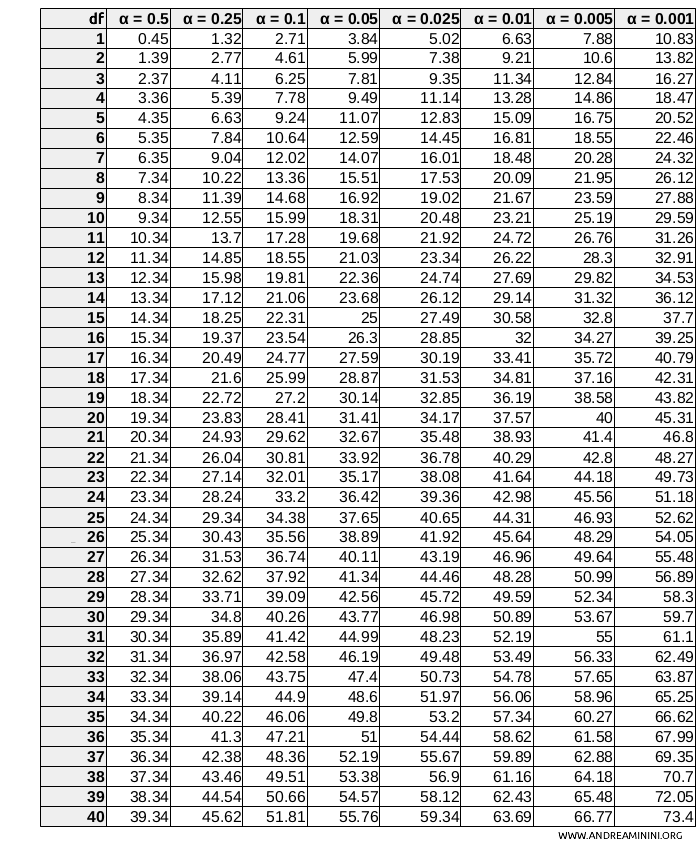
Infine, confronto il valore di \(\chi^2 = 16.67 \) con il valore critico ottenuto dalla tabella:
- Se il valore del \( \chi^2 \) è maggiore di 3.841 esiste una dipendenza significativa tra le variabili.
- Se il valore del \( \chi^2 \) è minore o uguale a 3.841 esiste una indipendenza tra le variabili.
In questo caso il valore di \(\chi^2 = 16.67 \) calcolato è maggiore del valore critico
$$ 16.67 > 3.841 $$
Questo significa che esiste una dipendenza significativa tra il genere e la preferenza per la materia. Non c'è indipendenza..
E così via.
