La distribuzione normale
Cos'è la distribuzione normale
La distribuzione normale è una distribuzione di probabilità caratterizzata da una curva a campana simmetrica. E' anche detta distribuzione gaussiana.
La curva a campana simmetrica è detta curva normale o curva di Gauss (o gaussiana).
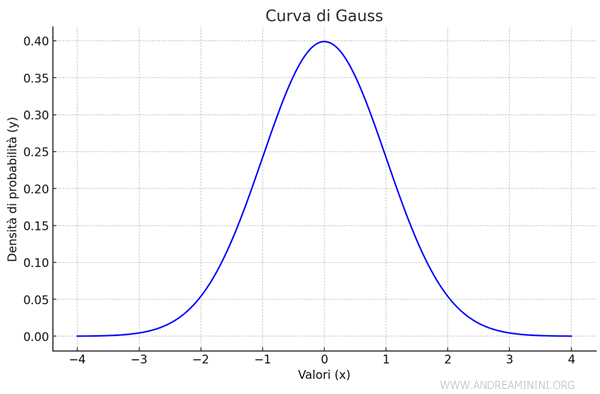
E' definita dalla media e dalla deviazione standard di una popolazione.
Nota. Il nome "gaussiana" deriva dal matematico tedesco Carl Friedrich Gauss, che la descrisse per la prima volta nel 1809. In genere si usa il termine "distribuzione normale" in matematica e statistica, mentre il termine "distribuzione gaussiana" è più utilizzato in fisica e ingegneria. Entrambi i termini si riferiscono alla stessa distribuzione di probabilità continua.
Come si calcola?
Per calcolare la distribuzione normale di una popolazione ho bisogno di due dati
Con questi due dati posso calcolare le probabilità dei valori.
A cosa serve?
Il calcolo della distribuzione normale mi fornisce informazioni sulla distribuzione delle probabilità dei valori che una variabile statistica può assumere.
Esempio. L'altezza delle persone della popolazione in una determinata fascia d'età può essere ben rappresentata dalla distribuzione normale perché gran parte delle persone hanno un'altezza vicina alla media. Va comunque detto che non tutti i fenomeni sono rappresentabili con la distribuzione gaussiana e, in ogni caso, è sempre presente un margine di incertezza nella rappresentazione.
Le caratteristiche della distribuzione gaussiana
In una distribuzione gaussiana il 68,27% dei valori è compreso tra M-σ e M+σ, dove M è la media aritmetica e σ è la deviazione standard.
Questo accade perché in una distribuzione gaussiana la deviazione standard è strettamente legata al modo in cui si distribuiscono le frequenze intorno al valore medio.
Si può dimostrare che:
- il 68,27% dei valori è compreso tra M-σ e M+σ ovvero entro una deviazioni standard dalla media
- il 95,45% dei valori è compreso tra M-2σ e M+2σ ovvero entro due deviazioni standard dalla media
- il 99,74% dei valori è compreso tra M-3σ e M+3σ ovvero entro tre deviazioni standard dalla media
Per raggiungere il 99,99% dei valori dovrei considerare un margine pari M-3,29σ e M+3,29σ
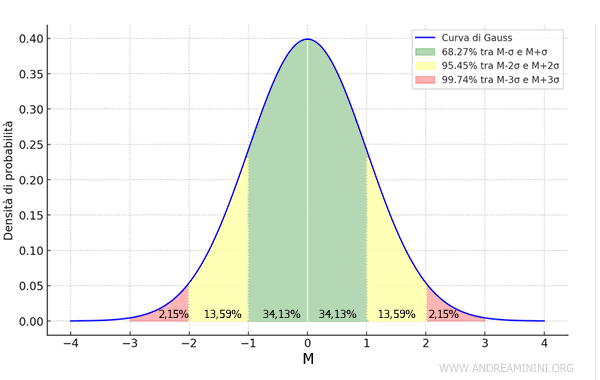
Si tratta una regola empirica conosciuta anche come "regola 68-95-99.7" della distribuzione di Gauss.
Nota. Il risultato ottenuto applicando questa regola a una distribuzione di dati è approssimato, perché le popolazioni non seguono perfettamente la distribuzione normale. Tuttavia, in alcuni fenomeni il risultato che ottengo è abbastanza accettabile.
I valori critici (z) della distribuzione normale
A ciascun livello di confidenza (o probabilità comulata) è associato un valore critico (z) che indicano quandi scarti standard ci si trova lontano dalla media per raccogliere una determinata percentuale dell'area sotto la curva.
Ad esempio, se il 68,27% dei valori è compreso tra M-σ e M+σ, il valore critico è z=1. Ciò significa che circa il 68,27% dei valori di una distribuzione normale standard si trova entro 1 deviazione standard dalla media $ M \pm \sigma $. Se il 95,45% dei valori è compreso tra M-2σ e M+2σ il valore critico è z=2. Se il 99,74% dei valori è compreso tra M-3σ e M+3σ il valore critico è z=3. E via dicendo.
Questi valori critici sono usati per costruire intervalli di confidenza e per altre applicazioni statistiche quando si assume che i dati siano distribuiti normalmente.
Ecco altri valori critici più comunemente utilizzati:
- 68.27% di confidenza: z=1
- 90% di confidenza: z=1,645
- 95% di confidenza: z=1,96
- 95.45% di confidenza: z=2
- 99% di confidenza: z=2,575
- 99.74% di confidenza: z=3
- 99,9% di confidenza: z=3,291
Per conoscere i valori critici (z) per un particolare livello di confidenza, diverso dai precedenti, bisogna consultare la tavola della distribuzione normale standard.
La funzione della densità
La formula generale della funzione di densità di probabilità di una distribuzione normale (curva di Gauss) è:
$$ f(x) = \frac{1}{\sigma \sqrt{2\pi}} \, e^{-\frac{(x - M)^2}{2 \sigma ^2}} $$
dove:
- \( M \) è la media della distribuzione,
- \( \sigma \) è la deviazione standard,
- \( x \) è la variabile casuale,
- \( e \) è la base del logaritmo naturale (\( \approx 2.718 \)).
Questa formula descrive come i valori della variabile \( x \) si distribuiscono attorno alla media \( M \), con una dispersione determinata dalla deviazione standard \(\sigma \).

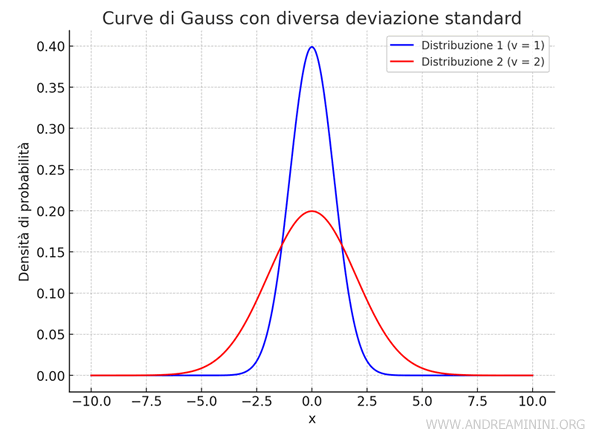
Il confronto tra due distribuzioni con la stessa media ma deviazione standard differente
Quando due distribuzioni hanno la stessa media \( M \) ma diversa deviazione standard \( \sigma \), la curva con una deviazione standard maggiore risulta essere più larga e schiacciata lungo l'asse orizzontale.
Questo accade perché la deviazione standard rappresenta la misura della dispersione dei dati intorno alla media: un valore maggiore indica che i dati sono più distribuiti, e quindi la curva sarà più ampia e bassa.
Al contrario, una deviazione standard più piccola implica che i dati sono più concentrati intorno alla media, il che rende la curva più stretta e alta.
Tuttavia, entrambe le curve mantengono la stessa area totale sotto di esse, che è pari a 1, poiché rappresentano distribuzioni di probabilità.
Questo comportamento visivo riflette l'effetto della deviazione standard sulla variabilità dei dati nella distribuzione.
Esempio. Considero due distribuzioni normali, entrambe con media \( M = 0 \), ma con diverse deviazioni standard:
- Distribuzione 1: \( M = 0 \) e \( v = 1 \)
- Distribuzione 2: \( M = 0 \) e \( v = 2 \)
Analizzo come queste distribuzioni appaiono graficamente e come la loro forma cambia in base alla deviazione standard.
- Distribuzione 1: \( N(0, 1) \)
La prima distribuzione ha una deviazione standard di 1. La sua funzione di densità di probabilità è: \[
f_1(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \] Questa distribuzione è centrata su \( M = 0 \) e i dati sono più concentrati attorno alla media. La curva sarà stretta e più alta. - Distribuzione 2: \( N(0, 2) \)
La seconda distribuzione ha una deviazione standard di 2. La sua funzione di densità di probabilità è: \[
f_2(x) = \frac{1}{2\sqrt{2\pi}} e^{-\frac{x^2}{8}} \] Anche questa distribuzione è centrata su \( M = 0 \), ma poiché la deviazione standard è maggiore, i dati sono più dispersi. La curva sarà più schiacciata orizzontalmente e più bassa.
Pertanto, la distribuzione 1 (con \( \sigma = 1 \)) sarà più stretta e concentrata, con una curva alta attorno alla media. La distribuzione 2 (con \( \sigma = 2 \)), invece, sarà più ampia e schiacciata, con una curva più bassa e dati più distribuiti.
Un esempio pratico
Considero una popolazione X composta da 100 studenti di cui conosco la media dell'altezza
$$ \mu=1,8 \ metri $$
e la deviazione standard
$$ \sigma^2 = 0,1 $$
A partire da questi dati voglio conoscere la probabilità per fasce di altezza
Scrivo una tabella con le altezze in ordine crescente da 1,65 a 2,00 metri
| altezza | densità di probabilità | cumulativa |
|---|---|---|
| 1,6 | ||
| 1,65 | ||
| 1,7 | ||
| 1,75 | ||
| 1,8 | ||
| 1,85 | ||
| 1,9 | ||
| 1,95 | ||
| 2,00 |
Quindi, calcolo la densità di probabilità normale e cumulativa usando la distribuzione normale.
| altezza | densità di probabilità | cumulativa |
|---|---|---|
| 1,6 | 0,54 | 0,02 |
| 1,65 | 1,30 | 0,07 |
| 1,7 | 2,42 | 0,16 |
| 1,75 | 3,52 | 0,31 |
| 1,8 | 3,99 | 0,50 |
| 1,85 | 3,52 | 0,69 |
| 1,9 | 2,42 | 0,84 |
| 1,95 | 1,30 | 0,93 |
| 2,00 | 0,54 | 0,98 |
La funzione della densità di probabilità mi fornisce un'idea sulla probabilità dei valori.
Ad esempio, i valori più vicini alla media aritmetica (μ=1,8) hanno una densità di probabilità maggiore.
Dal punto di vista grafico la distribuzione della densità di probabilità assume la classica forma di curva a campana simmetrica.
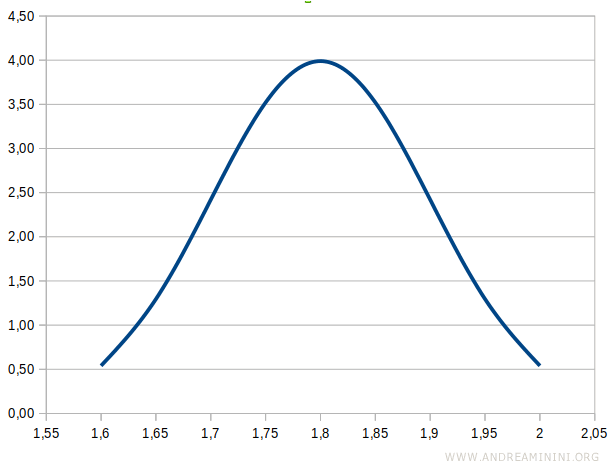
La curva della funzione di distribuzione cumulativa è invece una curva crescente da 0 a 1
Dove 0 e 1 misurano la probabilità.
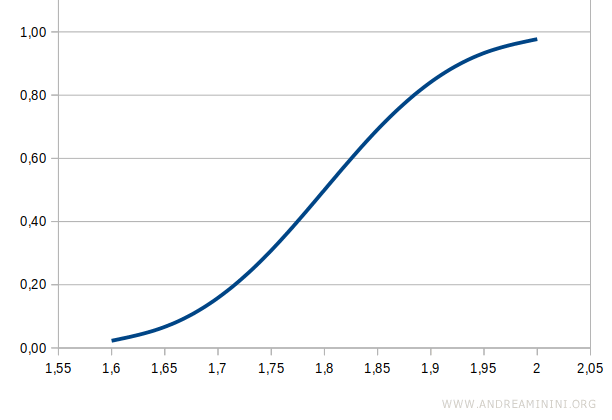
La funzione di distribuzione cumulativa mi permette di calcolare la probabilità per fascia di altezza.
Ad esempio, sapendo che la probabilità cumulativa fino a 1,7 metri è 0,16 e quella fino a 1,75 metri è 0,31, calcolo per differenza la probabilità della fascia 1,7-1,75
$$ p = 0,31 - 0,16 = 0,15 $$
Pertanto, la probabilità dell'altezza tra 1,7 e 1,75 metri è del 15%
Allo stesso modo posso calcolare le altre probabilità.
| altezza | probabilità | nota |
|---|---|---|
| 1,60 - 1.65 | 0,05 | 0,07-0,02 = 0,05 = 5% |
| 1-65 - 1,70 | 0,09 | 0,16-0,07 = 0,09 = 9% |
| 1,70 - 1,75 | 0,15 | 0,31-0,16 = 0,15 = 15% |
| 1,75 - 1,80 | 0,19 | 0,50-0,31 = 0,19 = 19% |
| 1,80 - 1,85 | 0,19 | 0,69-0,50 = 0,19 = 19% |
| 1,85 - 1,90 | 0,15 | 0,84-0,69 = 0,15 = 15% |
| 1,90 - 1,95 | 0,09 | 0,93-0,84 = 0,09 = 9% |
| 1,94 - 2,00 | 0,05 | 0,98-0,83 = 0,05 = 5% |
L'analisi campionaria
La distribuzione normale mi permette di studiare le caratteristiche di una popolazione osservando soltanto un campione della popolazione.
Cos'è un campione? E' un sottoinsieme di dati (o campione) selezionato in modo casuale dalla popolazione. L'obiettivo dell'analisi del campione è quello di trarre conclusioni sulla popolazione più ampia sulla base dei dati raccolti dal campione. Queste permette di ridurre i tempi e i costi dell'analisi statistica.
In questo caso il campione è composto da un numero "n" inferiore di elementi rispetto alla popolazione.
Per condurre l'analisi campionaria devo utilizzare:
- La media aritmetica del campione (μc)
- Le deviazione standard del campione (sc)
Nota. Nel caso dei campioni utilizzo il simbolo "s" per indicare la deviazione standard del campione. In modo da distinguerla dal simbolo σ che generalmente si utilizza per indicare la deviazione standard di una popolazione.
La media aritmetica del campione mi fornisce un'approssimazione della media aritmetica dell'intera popolazione.
In questo modo ottengo un'informazione sulla popolazione senza dover analizzare tutte le sue unità statistiche.
Nota. Ogni campione ha una media campionaria diversa dagli altri campioni. Pertanto, l'analisi campionaria è soggetta a un margine di incertezza che devo considerare.
Per calcolare l'incertezza dell'approssimazione posso utilizzare l'errore standard.
$$ s_x = \frac{s_c}{ \sqrt{n-1} } $$
Dove n è il numero di unità del campione e sc è la deviazione standard del campione.
L'errore standard mi permette di calcolare l'intervallo di confidenza.
$$ ( μ_c - 3 \cdot s_x \ , \ μ_c + 3 \cdot s_x ) $$
L'intervallo di confidenza è un intervallo che comprende al 99,74% il valore medio dell'intera popolazione.
Esempio. In una fabbrica che produce bulloni prelevo un campione di 50 bulloni per misurare il peso in grammi. La media aritmetica del campione è di 19,3 grammi e la deviazione standard campionaria è di 0,985. In questo caso l'errore standard è pari a 0,14 $$ s_x = \frac{0,985}{\sqrt{50-1}{}} = 0,14 $$ Pertanto, l'intervallo di confidenza è $$ (19,3 - 3 \cdot 0,14 \ , \ 19,3 + 3 \cdot 0,14 ) $$ $$ (18,88 \ , \ 19,72 ) $$Questo vuol dire che al 99,75% la media aritmetica del peso dei bulloni nell'intera popolazione è compresa tra 18,88 grammi e 19,72 grammi.
Se la stima riguarda una percentuale, per calcolare l'errore standard utilizzo una formula diversa
$$ s = \sqrt{ \frac{f \cdot (1-f) }{n} } $$
Anche in questo caso l'errore standard è inversamente correlato al numero di unità del campione (n).
Pertanto, quanto più aumenta la numerosità del campione, tanto più si riduce l'errore standard e l'ampiezza dell'intervallo di confidenza.
Esempio. In un urna ci sono un migliaio di palline. Estraggo un campione di 50 palline e ne osservo il colore. Il 30% delle palline sono rosse. Per proiettare questo dato sull'intera popolazione utilizzo la formula $$ s = \sqrt{ \frac{f \cdot (1-f) }{n} } $$ In questo caso f=0,30 e n=50 $$ s = \sqrt{ \frac{0,30 \cdot (1-0,30) }{50} } = \sqrt{ \frac{0,30 \cdot 0,70 }{50} } = \sqrt{ 0,21 }{50} = \sqrt{ 0,0042 } = 0,064 $$ L'errore standard è di 0,064 punti percentuali. Pertanto, l'intervallo di confidenza è compreso tra $$ (0,30 - 3 \cdot 0,064 \ , \ 0,30 + 3 \cdot 0,064 ) $$ $$ (0,30 - 0,192 \ , \ 0,30 - 0,192 ) $$ $$ (0,10,8 \ , \ 0,494 ) $$ Questo vuol dire che molto probabilmente, al 99,74%, la percentuale di palline rosse nell'intera popolazione è compresa tra il 10,8% e il 49,4%. L'intervallo è molto ampio. Per ridurlo dovrei prendere un campione con più palline. Ad esempio, estraggo n=200 palline e il 25% di queste sono rosse (f=0,25). Calcolo l'errore standard. $$ s = \sqrt{ \frac{0,25 \cdot (1-0,25) }{200} } = 0,0306 $$ In questo caso al 99,74% la popolazione delle palline rosse è compresa tra il 15,9% e il 34,1% $$ (0,25 - 0,0306 \cdot 3 \ , \ 0,25 + 0,0306 \cdot 3 ) $$ $$ (0,25 - 0,091 \ , \ 0,25 + 0,091 ) $$ $$ (0,159 \ , \ 0,341 ) $$ L'intervallo è ancora elevato ma è meno ampio rispetto al caso precedente.
E così via.
