Il coefficiente di correlazione lineare di Pearson
Il coefficiente di Pearson \( r \) misura la correlazione lineare tra due variabili. $$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} $$ dove \( X \) e \( Y \) sono le variabili osservate, e \( \bar{X} \) e \( \bar{Y} \) sono le loro rispettive medie.
Il coefficiente di Pearson è anche noto anche come coefficiente di correlazione di Bravais-Pearson,
E' un indicatore adimensionale, cioé non dipende dall'unità di misura e dalla scala delle variabili.
Il coefficiente di Pearson è un valore compreso tra -1 e 1, dove:
- r=1 indica una correlazione perfettamente positiva (o diretta), quando una variabile aumenta, l'altra aumenta in proporzione.
- r=-1 rappresenta una correlazione perfettamente negativa (o inversa), quando una variabile aumenta, l'altra diminuisce in proporzione
- r=0 segnala l’assenza di correlazione lineare tra le variabili.
Va sottolineato che il coefficiente di Pearson misura esclusivamente la correlazione lineare tra due variabili, quindi non rileva altri tipi di correlazioni, come quelle quadratiche, esponenziali o curvilinee.
Se le variabili sono legate in modo non lineare, il coefficiente di Pearson potrebbe risultare basso o nullo, anche se esiste una relazione forte tra le variabili.
La correlazione non va confusa con la causalità. La correlazione non implica causalità: due variabili possono essere correlate senza che una causi l’altra, perché potrebbero dipendere da una terza variabile. Allo stesso modo, l’assenza di correlazione non implica necessariamente assenza di causalità; una relazione causale può esistere, ma essere mascherata da altri fattori o da una relazione non lineare. Causalità e correlazione sono quindi concetti distinti: la correlazione misura un legame statistico, mentre la causalità implica un effetto diretto di una variabile sull’altra.
Un esempio pratico
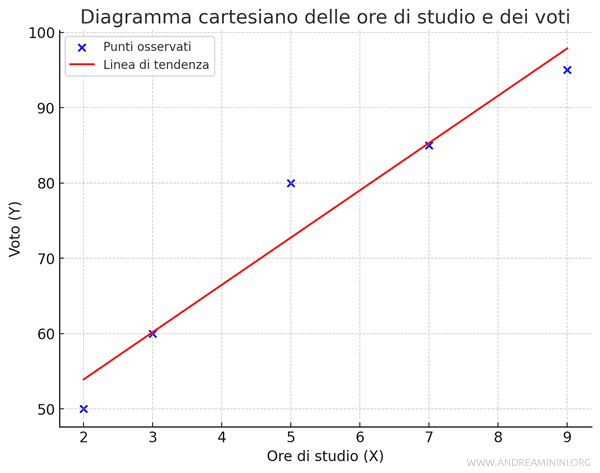
Prendo come esempio un piccolo dataset con due variabili: ore di studio (X) e voti agli esami (Y).
I dati raccolti per cinque studenti sono i seguenti:
| Studente | Ore di studio (X) | Voto (Y) |
|---|---|---|
| A | 2 | 50 |
| B | 3 | 60 |
| C | 5 | 80 |
| D | 7 | 85 |
| E | 9 | 95 |
Nota. In questo esempio l’analisi si basa su soli cinque studenti, il che rende il campione troppo piccolo per trarre conclusioni generali. E' però utile per rendere la spiegazione più semplice. In generale, un campione più ampio fornisce una visione più accurata della correlazione tra ore di studio e risultati accademici.
Calcolo le medie delle due variabili statistiche \( X \) e \( Y \)
$$ \bar{X} = \frac{2 + 3 + 5 + 7 + 9}{5} = 5.2 $$
$$ \bar{Y} = \frac{50 + 60 + 80 + 85 + 95}{5} = 74 $$
Per ciascun valore di \( X \) e \( Y \), calcolo le deviazioni dalla media, cioè \( X - \bar{X} \) e \( Y - \bar{Y} \), e i prodotti di queste deviazioni \( (X - \bar{X})(Y - \bar{Y}) \).
Inoltre, eleviamo al quadrato queste deviazioni per ottenere \( (X - \bar{X})^2 \) e \( (Y - \bar{Y})^2 \).
| Studente | \( X \) | \( Y \) | \( X - \bar{X} \) | \( Y - \bar{Y} \) | \( (X - \bar{X})(Y - \bar{Y}) \) | \( (X - \bar{X})^2 \) | \( (Y - \bar{Y})^2 \) |
|---|---|---|---|---|---|---|---|
| A | 2 | 50 | -3.2 | -24 | 76.8 | 10.24 | 576 |
| B | 3 | 60 | -2.2 | -14 | 30.8 | 4.84 | 196 |
| C | 5 | 80 | -0.2 | 6 | -1.2 | 0.04 | 36 |
| D | 7 | 85 | 1.8 | 11 | 19.8 | 3.24 | 121 |
| E | 9 | 95 | 3.8 | 21 | 79.8 | 14.44 | 441 |
Ora sommo i valori nelle colonne finali:
$$ \sum (X - \bar{X})(Y - \bar{Y}) = 206 $$
$$ \sum (X - \bar{X})^2 = 32.8 $$
$$ \sum (Y - \bar{Y})^2 = 1370 $$
Questo mi permette di calcolare il coefficiente di Pearson \( r \)
$$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \cdot \sum{(Y - \bar{Y})^2}}} $$
Sostituendo i valori nella formula ottengo:
$$ r = \frac{206}{\sqrt{32.8 \cdot 1370}} \approx 0.97$$
Il risultato, \( r \approx 0.97 \), indica una forte correlazione positiva tra le ore di studio e i voti.
Questo suggerisce che un maggior numero di ore di studio è associato a voti più alti.
Nota. Sebbene vi sia una correlazione forte, questo non implica necessariamente causalità. Fattori esterni, come la qualità dello studio o le capacità individuali, potrebbero influenzare i voti. Ad esempio, non è detto che più ore di studio portino automaticamente a voti più alti, poiché anche il modo di studiare è fondamentale.
Il calcolo del coefficiente di correlazione tramite i coefficienti di regressione
Il coefficiente di correlazione \( r \) di Pearson posso anche calcolarlo come la radice quadrata del prodotto dei coefficienti di regressione \( m \) e \( m_1 \) delle rette di regressione: $$ r = \pm \sqrt{m \cdot m_1} $$
Questa formula deriva dal fatto che il prodotto dei coefficienti di regressione è uguale al quadrato del coefficiente di correlazione \( r^2 \).
Il segno di \( r \) dipende dal segno di \( m \) e \( m_1 \):
- Se entrambi i coefficienti di regressione sono positivi, allora \( r \) sarà positivo.
- Se entrambi sono negativi, \( r \) sarà negativo.
Quindi, conoscendo i coefficienti di regressione (o pendenze) delle rette di regressione, posso ottenere anche il coefficiente di correlazione di Pearson tra le due variabili.
Nota. Se conosco \( r \) e le deviazioni standard \( \sigma_X \) e \( \sigma_Y \) posso calcolare direttamente le pendenze delle rette di regressione, che descrivono il cambiamento medio di una variabile rispetto all'altra.
- Il coefficiente di regressione di \( Y \) rispetto a \( X \) ossia $ y = m_1 x + q_1 $ $$ m_1 = r \frac{\sigma_Y}{\sigma_X} $$
- Il coefficiente di regressione di \( X \) rispetto a \( Y \) ossia $ x = m_2 y + q_2 $ $$ m_2 = r \frac{\sigma_X}{\sigma_Y} $$
Queste formule mostrano che i coefficienti di regressione sono proporzionali al coefficiente di correlazione \( r \), ma "scalati" dal rapporto tra le deviazioni standard di \( X \) e \( Y \).
Dimostrazione
Per ipotesi conosco i coefficienti di regressione di $ X $ e $ Y $
$$ m_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} $$
$$ m_2 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (y_i - \bar{y})^2} $$
Calcolo il prodotto \( m \cdot m_1 \) dei coefficienti di regressione.
$$ m \cdot m_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} \cdot \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (y_i - \bar{y})^2} $$
$$ m \cdot m_1 = \frac{\left[\sum (x_i - \bar{x})(y_i - \bar{y})\right]^2}{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2} $$
Questo risultato è uguale al quadrato del coefficiente di correlazione lineare di Pearson.
$$ m \cdot m_1 = r^2 $$
Pertanto, il coefficiente di Pearson è la radice quadrata del prodotto dei coefficienti di regressione.
$$ r = \pm \sqrt{m \cdot m_1}. $$
In questo caso, il segno di \( r \) devo sceglierlo in base al segno dei coefficienti di regressione.
- Il coefficiente \( r \) ha il segno \( + \) se i due coefficienti sono positivi
- Il coefficiente \( r \) ha il segno \( - \) se i due coefficienti sono negativi
Questo dimostra la relazione tra il coefficiente di Pearson e i coefficienti di regressione.
La relazione tra il coefficiente di Pearson, i coefficienti di regressione e la deviazione standard
Sapendo che il coefficiente di Pearson è
$$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} $$
Le deviazioni standard sono:
$$ \sigma_X = \sqrt{ \frac{1}{n} \cdot \sum (X- \bar{X})^2 } $$
$$ \sigma_Y = \sqrt{ \frac{1}{n} \cdot \sum (Y- \bar{Y})^2 } $$
Moltiplico il coefficiente di Pearson per il rapporto tra le deviazioni standard.
$$ m_1 = r \frac{\sigma_Y}{\sigma_X} $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \frac{ \sqrt{ \frac{1}{n} \cdot \sum (X- \bar{Y})^2 } }{ \sqrt{ \frac{1}{n} \cdot \sum (Y- \bar{X})^2 } } $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \sqrt{ \frac{1}{n} \cdot \sum (Y- \bar{Y})^2 \cdot \frac{n}{ \sum (X- \bar{X})^2 } } $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \sqrt{ \frac{ \sum (Y- \bar{Y})^2 }{ \sum (X- \bar{X})^2 } } $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \frac{ \sqrt{ \sum (Y- \bar{Y})^2 } }{ \sqrt{ \sum (X- \bar{X})^2 }} $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} } \cdot \sqrt{ \sum{(Y - \bar{Y})^2}}} \cdot \frac{ \sqrt{ \sum (Y- \bar{Y})^2 } }{ \sqrt{ \sum (X- \bar{X})^2 }} $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} } \cdot \sqrt{ \sum (X- \bar{X})^2 } } $$
$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{ \sum{(X - \bar{X})^2} } $$
In questo modo ho trovato il coefficiente di regressione di \( Y \) rispetto a \( X \) ossia $ y = m_1 x + q_1 $
Nota. Seguendo la stessa procedura posso dimostrare che ol coefficiente di regressione di \( X \) rispetto a \( Y \) ossia $ x = m_2 y + q_2 $ è $$ m_2 = r \frac{\sigma_X}{\sigma_Y} $$ Basta ribaltare il rapporto tra le deviazione standard e procedere con le semplificazioni algebriche.
Pro e contro del coefficiente di Pearson
Il coefficiente di Pearson presenta alcuni limiti importanti:
- Correlazione solo lineare
Rileva solo la relazione lineare tra due variabili, ignorando qualsiasi legame non lineare. Se esistono relazioni quadratiche, esponenziali o curvilinee, Pearson può risultare fuorviante. In questi casi, altre misure di correlazione, come quella di Spearman, o analisi specifiche delle curve, possono essere più appropriate. - Sensibilità agli outlier
È molto influenzato dai valori anomali, che possono distorcere il risultato e indicare una correlazione diversa dalla realtà dei dati principali. - Necessità di variabili quantitative e continue
Funziona solo con variabili su scale di intervallo o rapporto. Variabili categoriali o ordinali richiedono metodi alternativi come la correlazione di Spearman. - Distribuzione normale
La correlazione di Pearson è più efficace quando le variabili sono distribuite normalmente. In caso contrario, l’interpretazione del coefficiente può essere meno affidabile. - Nessuna causalità implicità
Come ogni misura di correlazione, Pearson non implica causalità; una correlazione elevata non significa che una variabile causa l’altra.
Il coefficiente di Pearson offre però anche diversi vantaggi:
- Interpretazione semplice
Fornisce un valore compreso tra -1 e 1, dove i valori estremi indicano una correlazione lineare perfetta, facilitando la comprensione della forza e della direzione della relazione. - Calcolo rapido
È relativamente semplice e veloce da calcolare, rendendolo una scelta pratica per analisi esplorative rapide. - Sensibilità alle variazioni lineari
È particolarmente utile quando si vogliono misurare e confrontare relazioni lineari tra variabili quantitative continue. - Facilita l'analisi preliminare
È uno strumento di analisi preliminare che aiuta a identificare potenziali relazioni tra variabili, guidando verso analisi più approfondite se necessario.
E così via.
