Correlazione
La correlazione in statistica misura la relazione tra due o più variabili, indicando se e come variano insieme. Se le variabili si muovono nella stessa direzione, si parla di correlazione positiva, se si muovono in direzioni opposte, si ha una correlazione negativa.
Per misurare la correlazione tra due variabili posso utilizzare la covarianza.
La covarianza restituisce un valore positivo o negativo che indica l'esistenza di una correlazione positiva o negativa tra i dati.
- Correlazione positiva
Se la covarianza è positiva, le due variabili sono correlate positivamente: quando una aumenta, anche l'altra tende a crescere. - Correlazione negativa
Se la covarianza è negativa, le variabili sono correlate negativamente: quando una aumenta, l'altra tende a diminuire.
Tuttavia, la covarianza non è un indicatore normalizzato perché viene influenzato dall'unità di misura dei dati e, quindi, è difficile interpretare il suo valore assoluto.
Per questa ragione la correlazione è spesso quantificata anche tramite il coefficiente di correlazione di Pearson, che assume valori standard compresi tra -1 e 1, dove:
- 1 indica una correlazione perfetta positiva,
- 0 indica assenza di correlazione,
- -1 indica una correlazione perfetta negativa.
Nota. La correlazione non va confusa con la causalità. Due variabili possono muoversi nella stessa direzione ma non essere legate da una relazione di causalità.
Un esempio pratico
In questo esempio considero due variabili \( X \) e \( Y \):
$$ X = [1, 2, 3, 4, 5] $$
$$ Y = [2, 4, 6, 8, 10] $$
Per misurare la correlazione calcolo la covarianza e il coefficiente di correlazione di Pearson.
Innanzitutto, calcolo la media di ciascuna variabile:
$$ \bar{X} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 $$
$$ \bar{Y} = \frac{2 + 4 + 6 + 8 + 10}{5} = 6 $$
Poi calcolo la covarianza. La formula della covarianza per due variabili \( X \) e \( Y \) è:
$$ \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y}) $$
Dove \( n \) è il numero di coppie (qui \( n = 5 \)).
Calcolo i singoli prodotti:
| $ X_i $ | $ Y_i $ | $ (X_i - \bar{X})(Y_i - \bar{Y}) $ | Risultato |
|---|---|---|---|
| 1 | 2 | (1−3)(2−6) | 8 |
| 2 | 4 | (2−3)(4−6) | 2 |
| 3 | 6 | (3−3)(6−6) | 0 |
| 4 | 8 | (4−3)(8−6) | 2 |
| 5 | 10 | (5−3)(10−6) | 8 |
Sommo i prodotti e trovo la covarianza.
$$ \text{Cov}(X, Y) = \frac{8 + 2 + 0 + 2 + 8}{5} $$
$$ \text{Cov}(X, Y) = \frac{20}{5} = 4.0 $$
La covarianza tra i dati è 4.0 e indica una probabile correlazione positiva tra i dati.
Tuttavia, la covarianza misura l'andamento comune di due variabili, ma non rappresenta direttamente la correlazione.
Nota. La covarianza indica se due variabili tendono a variare insieme (covarianza positiva) o in direzioni opposte (covarianza negativa) ma non è standardizzata e dipende dalle unità di misura delle variabili, rendendo difficile interpretare il suo valore assoluto.
Per ottenere un valore più interpretabile e confrontabile, calcolo anche il coefficiente di correlazione di Pearson, che è una versione normalizzata della covarianza.
Il coefficiente di Pearson è un indicatore compreso tra -1 e 1, e fornisce una misura più precisa della relazione lineare tra le variabili.
Si calcola con la seguente formula:
$$ r = \frac{\text{Cov}(X, Y)}{\sigma_X \cdot \sigma_Y} $$
Dove \( \sigma_X \) è la deviazione standard di \( X \) e \( \sigma_Y \) è la deviazione standard di \( Y \).
So già che la covarianza tra le variabili è $ \text{Cov}(X, Y) = 4.0 $
$$ r = \frac{4}{\sigma_X \cdot \sigma_Y} $$
Calcolo prima la deviazione standard \( \sigma_X \)
$$ \sigma_X = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(X_i - \bar{X})^2} $$
$$ \sigma_X = \sqrt{\frac{(1 - 3)^2 + (2 - 3)^2 + (3 - 3)^2 + (4 - 3)^2 + (5 - 3)^2}{5}}$$
$$ \sigma_X = \sqrt{\frac{4 + 1 + 0 + 1 + 4}{5}} = \sqrt{2} \approx 1.414 $$
Poi calcolo la deviazione standard \( \sigma_Y \):
$$ \sigma_Y = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(Y_i - \bar{Y})^2} $$
$$ \sigma_Y = \sqrt{\frac{((2 - 6)^2 + (4 - 6)^2 + (6 - 6)^2 + (8 - 6)^2 + (10 - 6)^2}{5}} $$
$$ \sigma_Y = \sqrt{\frac{16 + 4 + 0 + 4 + 16}{5}} = \sqrt{8} \approx 2.828 $$
Una volta ottenute le deviazioni standard \( \sigma_X \) e \( \sigma_Y \), posso calcolare il coefficiente di Pearson \( r \):
$$ r = \frac{4.0}{\sigma_X \cdot \sigma_Y} $$
$$ r = \frac{4.0}{1.414 \cdot 2.828} \approx 1.0 $$
In questo caso il coefficiente di Pearson è $ r \approx 1.0 $, questo conferma che le variabili $ X $ e $ Y $ hanno una correlazione positiva perfetta.
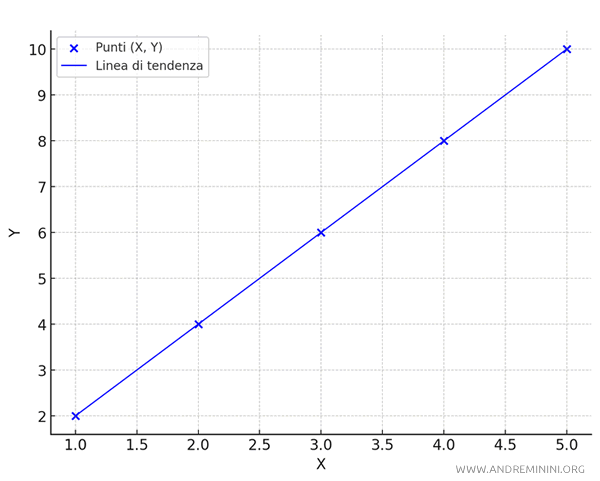
Quando la variabile $ X $ aumenta anche la variabile $ Y $ aumenta e viceversa.
La differenza tra correlazione e causalità
La correlazione e la causalità sono due concetti distinti.
- Correlazione: indica una relazione tra due variabili, cioè quando una varia, anche l'altra tende a variare in modo simile o opposto. Tuttavia, la correlazione non implica necessariamente che una variabile influenzi direttamente l'altra.
- Causalità: implica un rapporto di causa-effetto, ovvero una variabile (la causa) provoca un cambiamento nell'altra (l'effetto). Per stabilire la causalità, è necessario dimostrare che non solo le variabili sono correlate, ma che una è la causa dell'altra, escludendo altre spiegazioni possibili.
Quindi, anche se due variabili sono correlate, non significa automaticamente che una sia la causa dell’altra; potrebbero esserci fattori esterni o coincidenze.
In breve, la correlazione è osservare che due cose accadono insieme. La causalità è sapere perché accadono.
Esempio
Uno studio rileva che nei giorni in cui ci sono più gelati venduti, aumenta anche il numero di persone che annegano in piscina.
Potrei saltare alla conclusione che mangiare gelati provoca annegamenti? Sicuramente, no. In realtà, c’è una terza variabile in gioco: il caldo. Quando fa caldo, la gente mangia più gelati e va più spesso in piscina.
Quindi, il caldo è la vera causa di entrambe le cose, ma gelati (A) e annegamenti (B) sono solo correlati tra loro, non c’è nessun legame di causa-effetto diretto. Tra le due variabili A e B c'è una correlazione, non una causalità.
Questo è il punto: correlazione vuol dire soltanto che due cose succedono insieme. Causalità, invece, vuol dire che una cosa causa l’altra.
Esempio 2
Guardando la strada osservo che le persone portano l'ombrello e le strade sono bagnate.
Questi due eventi si presentano spesso insieme. Ma non è l’ombrello a bagnare la strada, né la strada bagnata a far comparire gli ombrelli, ovviamente. Sono due effetti della stessa causa: la pioggia.
La pioggia è il vero fattore causale, quello che effettivamente genera sia il fatto che la gente prenda l'ombrello sia il fatto che le strade diventino bagnate.
Quindi posso dire che c’è una relazione di causalità tra la pioggia e questi due eventi. Tra le persone che portano l'ombrello e la strada bagnata, invece, c'è solo una relazione di correlazione.
E così via.
