Gli indici di variabilità

Gli indici di variabilità misurano la dispersione e la disuguaglianza dei dati in una distribuzione statistica.

La variabilità dei dati è quantificabile in due aspetti diversi tra loro

• La dispersione è l'addensamento o meno dei valori rispetto a un valore medio x_M (o altro valore). La posso misurare tramite lo scarto o lo scostamento medio dei valori x_i-x_M
• La disuguaglianza è la differenza di valore dei dati. La misuro osservando le differenze in valore assoluto |x_i-x_j| tra tutti gli elementi della popolazione presi a coppia.

Nota. Gli indici di variabilità sono usati in statistica per confrontare due o più distribuzioni o popolazioni statistiche. Ad esempio, se ho due gruppi A e B con la stessa media ma il gruppo B ha minore dispersione, vuol dire che i dati del secondo gruppo sono più concentrati intorno al valore medio rispetto al primo gruppo.

A cosa servono gli indici di variabilita

Quando utilizzo un indice di posizione (es. la media aritmetica) ottengo una informazione sintetica della distribuzione perdendo però molte altre informazioni.

Tra le informazioni perdute c'è quella sulla variabilità dei dati.

Ad esempio, considero due gruppi di studenti e misuro la loro altezza.

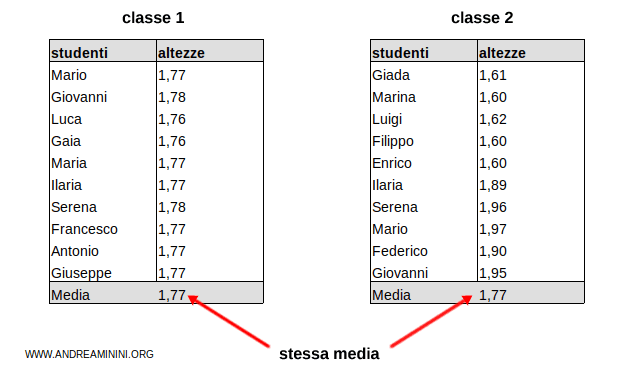
In entrambi i casi la media aritmetica è uguale a 1,77 cm ... ma le popolazioni statistiche non sono uguali.

$$ \mu=1,77 \ cm $$

E' un indice di sintesi che non mi dice nulla sulla variabilità dei dati.

• Nel primo gruppo (classe 1) gli studenti hanno tutti un'altezza vicina alla media (1,77)
• Nel secondo gruppo (classe 2) gli studenti hanno altezze molto diverse dalla media (1,77).

Per questa ragione, è molto utile accompagnare un indice di sintesi con un indice di variabilità.

Tipi di indici di variabilità

Esistono due tipologie di indici di variabilità

• Gli indici di variabilità assoluta
  Questi indici dipendono dall'unità di misura dei dati. Ad esempio, la varianza o lo scarto quadratico medio.
  • Il campo di variazione
    Misura la differenza tra il valore massimo e il valore minimo della distribuzione.
  • La differenza interquartile
    Misura la differenza Q₃-Q₁ tra il terzo quartile (Q₃) e il primo quartile (Q₁) di una distribuzione.
    La semidifferenza interquartile
    Misura la metà della differenza interquartile
  • Lo scostamento semplice medio
    Somma il valore assoluto degli scarti rispetto alla media o alla mediana
  • La varianza
    Misura la dispersione statistica
  • La varianza campionaria
    Misura la dispersione statistica della popolazione tramite un campione
  • La deviazione standard (scarto quadratico medio)
    Calcola la radice quadrata della varianza
  • La deviazione standard campionaria
    Calcola la radice quadrata della varianza campionaria
  • La devianza
    Misura la dispersione statistica
  • La differenza media
    Misura la distanza interna tra gli elementi di una distribuzione.
• Gli indici di variabilità relativa
  Sono indici che non dipendono dall'unità di misura dei dati. Sono molto utili per confrontare la variabilità di due fenomeni diversi tra loro.
  • Il coefficiente di variazione
    Misura la variabilità relativa di una o più distribuzioni
  • La concentrazione
    Misura la concentrazione della variabilità
  • Le variabili standardizzate

E così via.