Diagramma cartesiano
Il diagramma cartesiano è una rappresentazione grafica dei dati che permette di visualizzare la relazione tra due variabili statistiche su un piano (detto piano cartesiano).
Per costruire un diagramma cartesiano assegno le variabili agli assi del piano
- Asse orizzontale (asse delle ascisse o asse x)
L'asse x rappresenta una variabile statistica. - Asse verticale (asse delle ordinate o asse y)
L'asse y rappresenta l'altra variabile statistica.
Entrambi gli assi hanno un verso indicato da una freccia e si intersecano in un punto detto origine (O) del diagramma cartesiano.
Nota. Generalmente sull'asse x viene indicata la variabile indipendente, come il tempo o la distanza, mentre sull'asse y è indicata la variabile dipendente, cioè quella che cambia in funzione della variabile sull'asse x.
Ogni punto P su questo piano è identificato da una coppia di valori numerici (x, y), detta coordinata cartesiana, che indica quanto ci si sposta lungo l'asse x e quanto lungo l'asse y.
Ad esempio, se ho un punto alle coordinate (3, 4), questo significa che devo spostarmi di +3 unità a destra lungo l'asse x e di +4 unità verso l'alto lungo l'asse y.
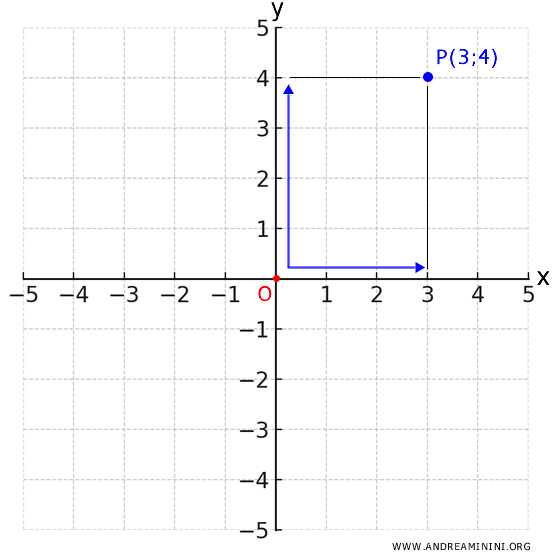
Un esempio pratico
Devo rappresentare le vendite di libri di un negozio nel corso di alcuni anni e voglio rappresentare questi dati su un diagramma cartesiano.
Ecco i dati delle vendite per ciascun anno:
| Anno | Libri Venduti |
|---|---|
| 2005 | 120 |
| 2006 | 140 |
| 2007 | 160 |
| 2008 | 130 |
| 2009 | 180 |
| 2010 | 150 |
| 2011 | 170 |
| 2012 | 100 |
| 2013 | 220 |
| 2014 | 190 |
| 2015 | 210 |
| 2016 | 250 |
Comincio a costruire il diagramma cartesiano.
Per prima cosa assegno le variabili agli assi cartesiani
- Sull'asse x (orizzontale) indico glli anni del periodo che sto analizzando (2005-2016)
- Sull'asse y (verticale) misuro le vendite ossia il numero di libri venduti.
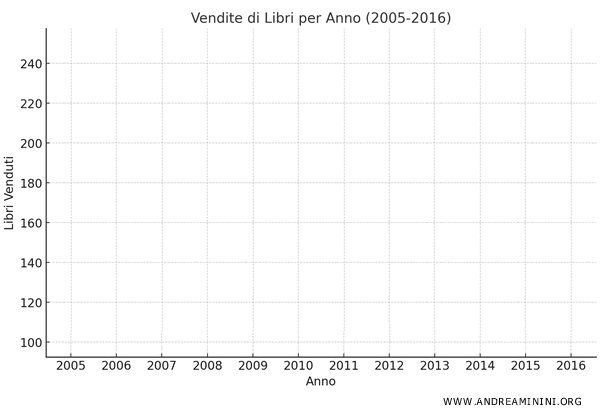
Nota. È fondamentale ricordarsi di specificare quali variabili sono rappresentate sull'asse x e sull'asse y. Senza questa indicazione, il grafico perde di significato. Si tratta di un errore comune, ma altrettanto serio, soprattutto se il grafico è parte di un esercizio d'esame.
Ogni punto sul diagramma cartesiano sarà rappresentato dalla coppia di coordinate (x, y), dove:
- La variabile $ x $ è l'anno
- La variabile $ y $ è il numero di libri venduti.
Considerando i dati nella tabella, le coordinate cartesiane per ciascun anno saranno le seguenti:
- (2005, 120) per l'anno 2005
- (2006, 140) per l'anno 2006
- (2007, 160) per l'anno 2007
- (2008, 130) per l'anno 2008
- (2009, 180) per l'anno 2009
- (2010, 150) per l'anno 2010
- (2011, 170) per l'anno 2011
- (2012, 200) per l'anno 2012
- (2013, 220) per l'anno 2013
- (2014, 190) per l'anno 2014
- (2015, 210) per l'anno 2015
- (2016, 250) per l'anno 2016
Disegno questi punti sul diagramma cartesiano.
Ad esempio, la coppia (2005,120) equivale a un punto che corrisponde all'anno 2005 sull'asse x e alla riga che interseca il valore 120 delle vendite sull'asse y.
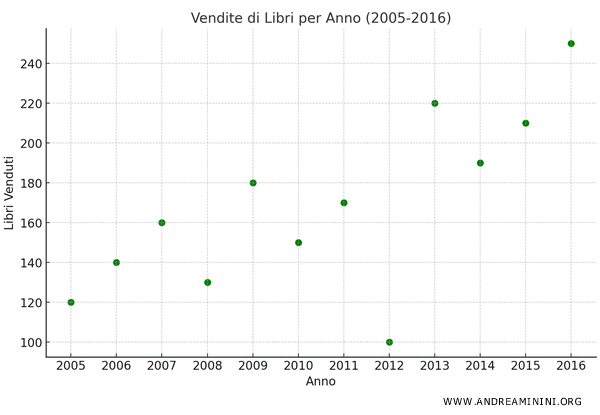
Questo insieme di punti forma una sorta di nuvola di punti.
Per rendere più chiaro l'andamento, unisco i punti adiacenti con una linea.
In questo modo ottengo un grafico a linee, detto anche poligono delle frequenze, che mostra la distribuzione delle frequenze, ovvero l'andamento delle vendite di libri nel corso degli anni.
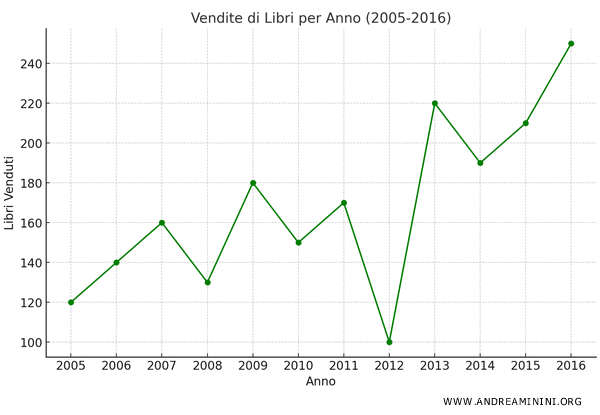
Questa rappresentazione grafica dei dati rende più facile interpretare l'andamento di un fenomeno nel corso del tempo e comprendere cosa sta accadendo.
In particolar modo, è molto utile per rappresentare visivamente una serie storica di dati.
Ad esempio, osservando il grafico posso vedere chiaramente come le vendite fluttuino nel corso del tempo. In questo caso è evidente che si stia verificando un aumento graduale delle vendite, nonostante una brusca caduta delle vendite registrata nel 2012. L'analisi induce a indagare sulle cause della caduta e su cosa non abbia funzionato nel 2012.
In alternativa, posso evidenziare i punti sul piano tracciando un segmento corrispondente alle ordinate.
Questo tipo di diagramma cartesiano è detto diagramma a segmenti.
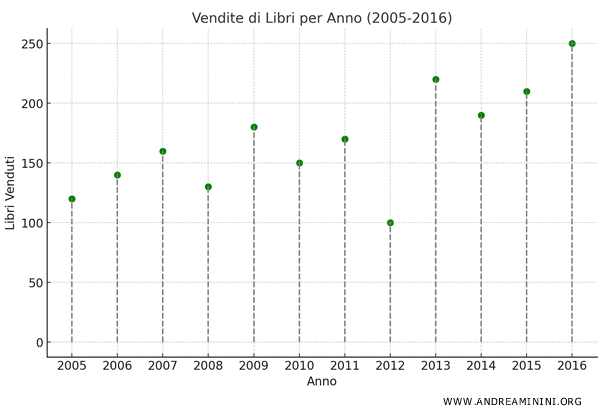
E così via.
