Trasformata di Laplace
La trasformata di Laplace converte una funzione reale f(t) in una funzione di variabile complessa F(s).
Data una funzione f(t) reale e nulla per t<0, la trasformata di Laplace F(s) è la seguente: $$ F(S) = L[f(t)] = \int_{0}^{∞} \: e^{-st} f(t) \: dt $$
La formula precedente è anche detta trasformata di Laplace fondamentale perché dà origine a molte regole di trasformazione.
A cosa serve la trasformata di Laplace
La trasformata di Laplace è usata per la risoluzione delle equazioni differenziali.
Semplifica le operazioni differenziali trasformandole in semplici equazioni algebriche.
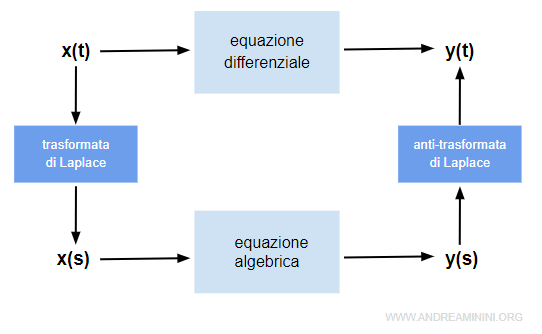
Una volta trovata la soluzione algebrica y(s) posso trasformarla in una funzione nel dominio del tempo y(t) tramite l'anti-trasformata di Laplace.
Pertanto, la trasformata di Laplace mi evita di dover svolgere parecchi calcoli molto più complessi.
Nota. La trasformata di Laplace mi permette anche di trovare direttamente la soluzione particolare che soddisfa una determinata condizione iniziale del sistema. Con i metodi tradizionali dovrei trovare prima la soluzione generale e poi quella la soluzione particolare svolgendo molti più calcoli. E' un altro vantaggio da considerare.
Come calcolare la trasformata di Laplace
La trasformata di Laplace si calcola con la seguente formula:
$$ F(s) = L[f(t)] = \int_{0}^{∞} \: e^{-st} f(t) \: dt $$
Nota. In alcuni libri la trasformata di Laplace è indicata anche con il simbolo L[f(t)]. E' la stessa cosa. $$ F(s)=L[f(t)] $$
La variabile s è una funzione complessa s=σ±jω ( pulsazione complessa ) detta operatore di Laplace con dimensioni inverse di un tempo [t-1].
$$ s=σ±jω $$
La funzione f(t) è invece una funzione reale in relazione al tempo t.
Perché l'integrale parte da t=0?
L'intervallo di integrazione comincia da t=0 perché generalmente la trasformata di Laplace si utilizza per studiare l'evoluzione di un fenomeno fisico a partire da un istante iniziale.
I fenomeni fisici evolvono in avanti nel tempo.
E' quindi inutile considerare l'intervallo negativo (t<0) della funzione f(t).
Nota. La trasformata di Laplace è particolarmente utile nella teoria dei sistemi perché consente di semplificare e svolgere algebricamente dei calcoli integro-differenziali altrimenti molto difficili. Trasforma le funzioni nel dominio del tempo f(t) in funzioni F(s) nel campo dei numeri complessi. Una volta risolta l'equazione algebrica nel campo complesso (s) posso trasformare il risultato in funzione del tempo f(t) tramite l'antitrasformata L-1.
Un esempio pratico
Ho la seguente equazione differenziale
$$ y'+y =-1 $$
La condizione iniziale è
$$ y(0)=0 $$
Nota. Per semplicità scrivo la funzione soltanto con il simbolo y anziché y(t). In ogni caso, la variabile indipendente è il tempo t>0.
Devo trovare la funzione y incognita.
Applico la traformata di Laplace a entrambi i membri dell'equazione.
$$ L[y'+y] =L[-1] $$
$$ L[y']+L[y] =L[-1] $$
So già che la trasformata di una costante è 1/s.
$$ L[y']+L[y] = -\frac{1}{s} $$
Ora applico il teorema della linearità e sostituisco la trasformata della derivata L[y'] con sL[y]-y(0)
$$ sL[y]+y(0)+L[y] = -\frac{1}{s} $$
So già che la condizione iniziale y(0)=0
$$ sL[y]+L[y] = -\frac{1}{s} $$
Poi raccolgo algebricamente L[Y]
$$ L[y](s+1) = -\frac{1}{s} $$
Quindi risolvo rispetto a L[y]
$$ L[y] = -\frac{1}{s(s+1)} $$
Una volta ottenuta la trasformata di Laplace, posso calcolare la funzione y(t) tramite l'antitrasformata di Laplace L-1.
$$ y(t) = L^{-1}[y] $$
$$ y(t) = L^{-1}[-\frac{1}{s(s+1)}] $$
Decompongo la frazione nel secondo membro
$$ y(t) = L^{-1}[\frac{1}{s+1}] - L^{-1}[\frac{1}{s}]$$
Ora calcolo l'antitrasformata dei singoli componenti
$$ y(t) = e^{-t} -1 $$
Ho così trovato la soluzione che cercavo
$$ y(t) = e^{-t} -1 $$
La trasformata di Laplace in elettronica
Il metodo della trasformata di Laplace è particolarmente utile nello studio delle reti con componenti reattivi (condensatori e induttori) in regime sinusoidale, perché semplifica il calcolo matematico sulle tensioni e le correnti.
Senza il metodo di Laplace dovrei studiare le correnti, le tensioni e la reazione ai segnali di ingresso dei componenti nel tempo tramite equazioni differenziali, integrali e derivate.
Ecco un esempio di equazione differenziale di un semplice circuito RC.
$$ v(t) = R \cdot i(t) + \frac{1}{C} \int{i(t) \: dt} $$
La trasformata di Laplace invece si basa su operazioni più semplici.
Le funzioni del tempo sono convertite in funzioni complesse con parte reale e immaginaria, questo mi permette di trasformare le equazioni integro-differenziali in semplici equazioni algebriche.
La L-trasformata del circuito RC precedente.
$$ \frac{E}{s} = R \cdot I(s) + \frac{1}{sC} I(s) $$
Nota. In una pagina a parte ho appuntato tutti i passaggi dell'analisi del circuito RC con la trasformata di Laplace.
La trasformata di Laplace mi permette di studiare più facilmente la reazione di un componente elettrico nella fase transitoria, quando reagisce a un segnale di ingresso.
E così via.
