Le trasformate di Laplace tipiche
Nella teoria dei sistemi alcune trasformate di Laplace sono più ricorrenti di altre. Sono dette segnali tipici o segnali saggio. Sono ottenute dalla seguente formula:
$$ L(t^ne^{at}) = \frac{n!}{(s-a)^{n+1}} $$
Dove n è un intero positivo, a una costante reale o complessa e t la variabile tempo non negativa.
A cosa servono? Ricordare queste trasformate evita di dover calcolare matematicamente la trasformata di Laplace ogni volta che si studia un sistema.
Elenco delle trasformate
Impulso unitario di Dirac
$$ L[δ(t)] = 1 $$
Un esempio di impulso unitario
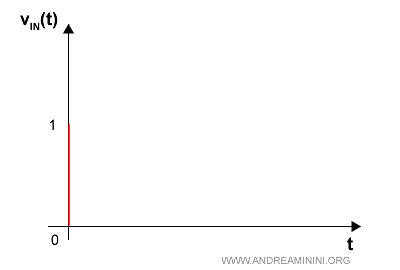
Gradino unitario
$$ L[u(t)] = L[1] = \frac{1}{s} $$
Si ottiene ponendo n=0 e a=0.
Un esempio di gradino unitario
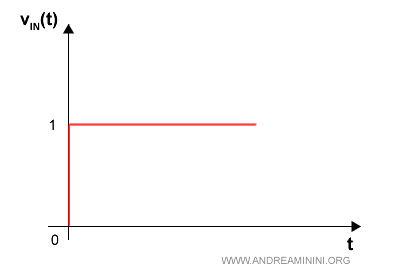
Gradino di ampiezza E
$$ L[u(t)] = L[E] = \frac{E}{s} $$
Un esempio di gradino di ampiezza costante E
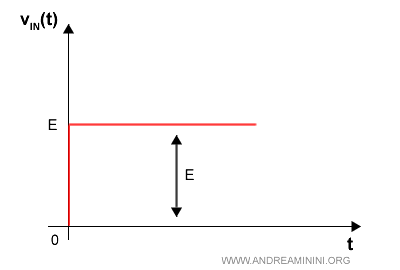
Rampa unitaria
$$ L[t] = \frac{1}{s^2} $$
Si ottiene ponendo n=1 e a=0.
Un esempio di segnale a rampa unitaria
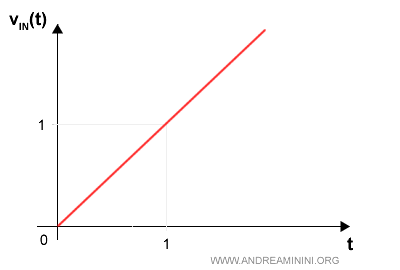
Rampa con pendenza k
Altre rampe con pendenza diversa da 1.
$$ L[k·t] = k·L(t) = \frac{k}{s^2} $$
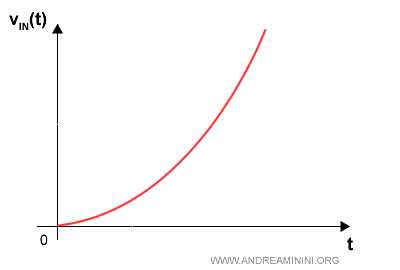
Parabola unitaria
$$ L[\frac{t^2}{2}] = \frac{1}{s^3} $$
Si ottiene ponendo n=2 e a=0 dividendo entrambi i membri per 2.
Nota. In generale, la trasformata dell'impulso unitario, del gradino unitario, della rampa unitaria e della parabola unitaria sono casi particolari della trasformata di un polinomio $$ L[ \frac{t^{k}}{k!}] = \frac{1}{s^{k+1}} $$
Potenza
$$ L[t^n] = \frac{n!}{s^{n+1}} $$
Esponenziale
$$ L[e^{at}] = \frac{1}{s-a} $$
$$ L[e^{-at}] = \frac{1}{s+a} $$
Si ottiene ponendo n=0.
Sinusoide
$$ L[\sin ωt] = \frac{ω}{s^2+ω^2} $$
Cosinusoide
$$ L[\cos ωt] = \frac{s}{s^2+ω^2} $$
Altre trasformate
$$ L[\frac{t^{n-1}}{(n-1)!}] = \frac{1}{s^n} $$
con n intero ed e>0
$$ L[\frac{1}{a}(1-e^{-at})] = \frac{1}{s(s+a)} $$
$$ L[\frac{e^{-at}-e^{-bt}}{b-a}] = \frac{1}{(s+a)(s+b)} $$
$$ L[t \cdot e^{-at}] = \frac{1}{(s+a)^2} $$
$$ L[\frac{1}{(n-1)!}(t^{n-1}e^{-at})] = \frac{1}{(s+a)^n} $$
$$ L[e^{-at} \sin ωt] = \frac{ω}{(s+a)^2+ω^2} $$
$$ L[\frac{k}{ω} e^{-at} \sin (ωt+φ)] = \frac{s+b}{(s+a)^2+ω^2} $$
Nota. con $$ φ=artg( \frac{ω}{b-a}) \\ k=\sqrt{(b-a)^2+ω^2} $$
E così via.
