Esempio di trasformata di Laplace con scomposizione e traslazione del segnale

Ho un segnale di ingresso f(t) che si presenta in questa forma:

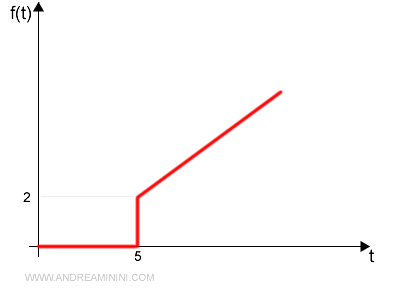
Per calcolare la trasformata di Laplace del segnale, considero il segnale come la somma di un segnale a gradino f₁ e di un segnale a rampa f₂.

Entrambi i segnali li ritardo di 5 secondi per farli coincidere con la funzione f(t).

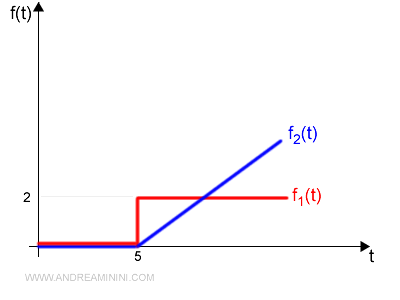
La funzione f(t) è la somma dei due segnali

$$ f(t) = f_1(t) + f_2(t) $$

A questo punto calcolo la trasformata di Laplace

$$ L[f(t)] = L[f_1(t) + f_2(t)] $$

Per il teorema della somma delle trasformate

$$ L[f(t)] = L[f_1(t)] + L[f_2(t)] $$

$$ F(s) = L[f_1(t)] + L[f_2(t)] $$

Calcolo la trasformata di Laplace della prima funzione f₁

$$ F(s) = \frac{2}{s} e^{-5s} + L[f_2(t)] $$

Spiegazione. Il primo segnale f₁ è un gradino di ampiezza E=2. Si tratta di un segnale tipico di cui già conosco la L-trasformata. $$ \frac{E}{s} $$ In questo caso devo però considerare anche un ritardo di t₀=5 secondi. Secondo il teorema della traslazione la formula precedente diventa $$ \frac{E}{s} e^{-t_0s} $$

Poi calcolo la trasformata di Laplace della seconda funzione f₂

$$ F(s) = \frac{2}{s} e^{-5s} + \frac{1}{s^2} e^{-5s} $$

Spiegazione. Il secondo segnale f₂ è una rampa a 45°. Pertanto il coefficiente angolare è α=1. E' un segnale tipico (rampa unitaria) di cui conosco la L-trasformata. $$ α \cdot \frac{1}{s^2} $$ Anche in questo caso devo considerare il ritardo di t₀=5 secondi e secondo il teorema della traslazione la formula precedente diventa $$ α \cdot \frac{1}{s^2} e^{-t_0s} $$

Dopo qualche semplice passaggio algebrico

$$ F(s) = e^{-5s} (\frac{2}{s}+\frac{1}{s^2} ) $$

ottengo la trasformata di Laplace della funzione f(t)

$$ F(s) = e^{-5s} (\frac{2s+1}{s^2} ) $$

E così via.