Come trovare la trasformata di Laplace di una funzione
Devo studiare una funzione f(t) nel tempo di cui conosco solo il grafico con la trasformata di Laplace.
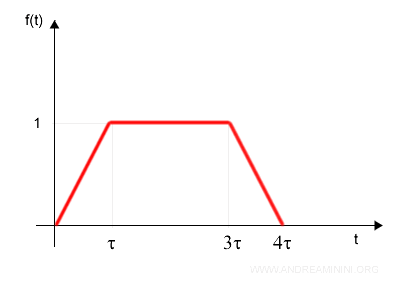
Posso considerare la funzione f(t) come la somma di quattro funzioni
$$ f(t) = \frac{1}{τ} \cdot [ t \cdot u(t) - (t-τ) \cdot u(t-τ) \\ - (t-3τ) \cdot u(t-3τ) + (t-4τ) \cdot u(t-4τ) ] $$
Nota. Dove u(t) è una qualsiasi funzione a cui è applicato il segnale di ingresso f(t).
perché il grafico è suddivisibile in quattro intervalli
- da 0 a τ è una rampa crescente
- da τ a 3τ è costante
- da 3τ a 4τ è una rampa decrescente
- da 4τ in poi è costante
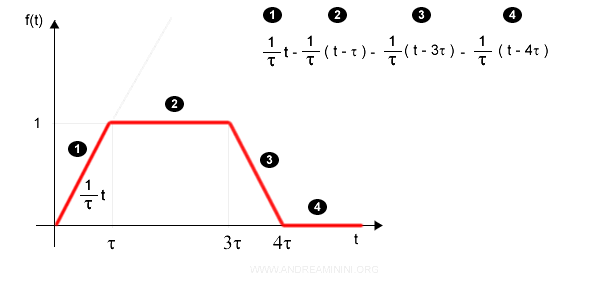
Intervallo da 0 a τ
In questo lasso di tempo ( punto 1 ) la funzione f(t) è una semplice rampa crescente di ampiezza 1 e pendenza 1/τ. La L-trasformata è la seguente:
$$ \frac{1}{τs^2} $$
Intervallo da τ a 3τ
In questo lasso di tempo ( punto 2 ) la funzione f(t) ha un andamento costante.
Per trasformare il segnale in uscita in una costante devo sottrarre la stessa rampa con segno opposto, perché nell'intervallo (τ-3τ) continua a esserci la rampa crescente del precedente intervallo.
Questa seconda funzione è traslata nel tempo con un ritardo pari a τ. Quindi, applico anche il teorema della traslazione.
$$ ( - \frac{1}{τs^2} ) e^{-sτ} $$
Nota. Complessivamente il segnale della funzione f(t) è $$ \frac{1}{τs^2} - \frac{1}{τs^2} e^{-sτ} $$
Intervallo da 3τ a 4τ
In questo lasso di tempo ( punto 3 ) la funzione f(t) è una rampa decrescente con pendenza 1/τ.
Per modificare il segnale di uscita ( costante ) in decrescente aggiungo una rampa decrescente traslata con un ritardo pari a 3τ.
$$ ( - \frac{1}{τs^2} ) e^{-s3τ} $$
Nota. Complessivamente il segnale della funzione f(t) è $$ \frac{1}{τs^2} - \frac{1}{τs^2} e^{-sτ} - \frac{1}{τs^2} e^{-s3τ} $$
Intervallo da 4τ in poi
In questo intervallo ( punto 4 ) la funzione torna costante.
Essendo il segnale di uscita una rampa decrescente, aggiungo il segnale di una rampa crescente traslato con un ritardo pari a 4τ.
$$ ( \frac{1}{τs^2} ) e^{-s4τ} $$
Nota. Complessivamente il segnale della funzione f(t) è $$ \frac{1}{τs^2} - \frac{1}{τs^2} e^{-sτ} - \frac{1}{τs^2} e^{-s3τ} + \frac{1}{τs^2} e^{-s4τ} $$
La L-Trasformata
Una volta trovate le L-Trasformate delle funzioni che compongono il segnale, non mi resta altro da fare che sommarle.
$$ L[f(t)] = \frac{1}{τs^2} + ( - \frac{1}{τs^2} ) e^{-sτ} + ( - \frac{1}{τs^2} ) e^{-s3τ} + ( \frac{1}{τs^2} ) e^{-s4τ} $$
$$ L[f(t)] = \frac{1}{τs^2} ( 1 - e^{-sτ} - e^{-s3τ} + e^{-s4τ} ) $$
Ho così trovato la trasformata di Laplace della funzione.
E così via.
