Circuito RC e trasformata di Laplace
Analisi della corrente
Ho un circuito RC composto da un generatore di tensione, un resistore e un condensatore.
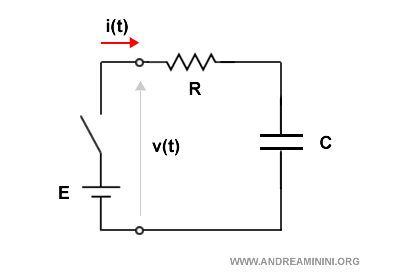
L'interruttore genera un impulso a gradino che porta la tensione da 0 a E.

Nota. Il passaggio da 0 a t è detto fase transitoria mentre l'intervello successivo è detto fase a regime.
Per studiare il comportamento del circuito nel tempo, nella fase transitoria e a regime, devo calcolare l'equazione del circuito.
$$ v(t) = v_R(t)+v_C(t) $$
Per semplicità non considero l'energia immagazzinata nel condensatore, la ipotizzo nulla.
Sapendo che in funzione del tempo le tensioni degli elementi sono:
$$ v_R(t)=R \cdot i(t) $$
$$ v_C(t)=\frac{1}{C} \int{i(t) \: dt} $$
Ottengo l'equazione differenziale del circuito elettrico RC in relazione al tempo.
$$ v(t) = R \cdot i(t) + \frac{1}{C} \int{i(t) \: dt} $$
Per evitare il calcolo differenziale, ricorro alla trasformata di Laplace.
Nota. La trasformata di Laplace mi permette di trasformare l'equazione differenziale in equazione algebrica, decisamente più semplice da risolvere.
La trasformata di Laplace del circuito RC
La trasformata di Laplace del circuito è
$$ L[v(t)]=V(s) $$
$$ L[R \cdot i(t) + \frac{1}{C} \int{i(t) \: dt}]=V(s) $$
$$ L[R \cdot i(t)] + L[\frac{1}{C} \int{i(t) \: dt}]=V(s) $$
Sostituisco le L-trasformate del resistore e del condensatore.
$$ R \cdot I(s) + \frac{1}{sC} I(s) =V(s) $$
A questo punto devo lavorare sul membro di destra dell'equazione e specificare il tipo di segnale in ingresso.
Si tratta di un impulso a gradino di ampiezza E ossia V(s)=E/s
$$ R \cdot I(s) + \frac{1}{sC} I(s) = \frac{E}{s} $$
Una volta creata l'equazione algebrica, la risolvo per trovare la corrente
$$ R \cdot I(s) + \frac{1}{sC} I(s) = \frac{E}{s} $$
$$ I(s) ( R + \frac{1}{sC} ) = \frac{E}{s} $$
$$ I(s) = \frac{E}{s ( R + \frac{1}{sC} ) } $$
Ho trovato la corrente I(s).
Ora per trovare la corrente in funzione del tempo, mi basta calcolare l'anti-trasformata di Laplace.
L'anti-trasformata di Laplace
L'equazione algebrica non è immediatamente convertibile tramite l'anti-trasformata di Laplace.
$$ L^{-1}[I(s)] = L^{-1}[ \frac{E}{s ( R + \frac{1}{sC} ) } ] $$
Con alcuni spostamenti algebrici ottengo
$$ L^{-1}[I(s)] = L^{-1}[ \frac{E}{R} \cdot \frac{1}{s+\frac{1}{RC}} ] $$
Applico il teorema della combinazione lineare della trasformata
$$ L^{-1}[I(s)] = L^{-1}[ \frac{E}{R} ] \cdot L^{-1}[ \frac{1}{s+\frac{1}{RC}} ] $$
In questa forma diventa più semplice calcolare l'anti-trasformata di ogni singola componente.
L'anti-trasformata di I(s) è i(t).
$$ i(t) = L^{-1}[ \frac{E}{R} ] \cdot L^{-1}[ \frac{1}{s+\frac{1}{RC}} ] $$
La componente E/R è una costante.
Posso applicare il teorema del prodotto di una L-trasformata per una costante.
$$ i(t) = \frac{E}{R} \cdot L^{-1}[ \frac{1}{s+\frac{1}{RC}} ] $$
Infine, l'ultima componente è una L-trasformata tipica.
Posso riscrivere l'equazione della corrente i(t) nella forma finale in relazione del tempo.
$$ i(t) = \frac{E}{R} \cdot e^{- \frac{t}{RC} } $$
Spiegazione. La L-trasformata di un esponenziale è $$ L[e^{-at}] = \frac{1}{s+a} $$ se considero a=1/RC diventa $$ L[e^{-\frac{t}{RC}t}] = \frac{1}{s+\frac{t}{RC}} $$
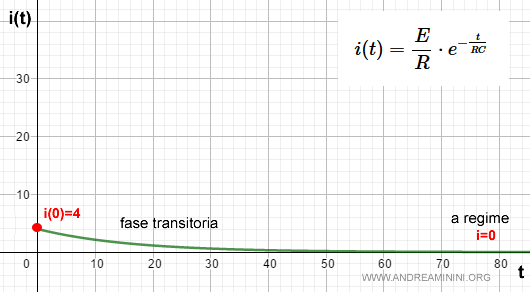
Quest'ultima formula spiega correttamente le variazioni della corrente dopo la chiusura dell'interruttore, nella fase transitoria e in quella a regime.
$$ i(t) = \frac{E}{R} \cdot e^{- \frac{t}{RC} } $$
Esempio. Se E=8, R=2 e C=2 quando t=0 l'esponenziale vale 1 e la corrente è uguale a i(0)=E/R=8/2=4. Nella fase transitoria, col passare del tempo, il condensatore accumula energia e riduce la corrente nel circuito. Nella fase a regime l'esponenziale tende a zero e la corrente nel circuito è nulla (i=0).
Analisi della tensione in uscita
Per analizzare la tensione ai capi del condensatore, aggiungo le incognite vin(t) e vout(t) della tensione di entrata e di uscita.
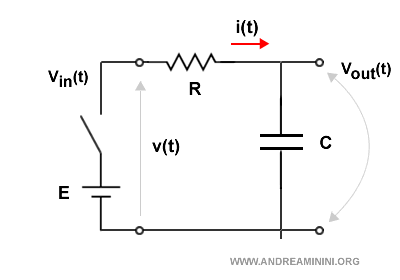
Poi scrivo l'equazione della maglia
$$ v_{in}(t)-Ri(t) - v_{out}(t)=0 $$
ossia
$$ v_{in}(t) = Ri(t) + v_{out}(t) $$
La corrente i(t) la posso prendere dal condensatore
$$ v_{in}(t) = R C \frac{d \: v_{out}(t)}{dt} + v_{out}(t) $$
Nota. La funzione nel tempo di un condensatore è $$ i(t)=C \frac{d \: v(t)}{dt} $$
E' l'equazione differenziale del circuito.
Calcolo la L-trasformata
$$ L[v_{in}(t)] = L[R C \frac{d \: v_{out}(t)}{dt} + v_{out}(t)] $$
Il segnale in ingresso è un segnale a gradino di ampiezza E
$$ \frac{E}{s} = L[R C \frac{d \: v_{out}(t)}{dt} + v_{out}(t)] $$
Applico il teorema della somma della trasformata
$$ \frac{E}{s} = L[R C \frac{d \: v_{out}(t)}{dt}] + L[v_{out}(t)] $$
La trasformata di Vout(t) è Vout(s)
$$ \frac{E}{s} = L[R C \frac{d \: v_{out}(t)}{dt}] + v_{out}(s) $$
Poi applico il teorema del prodotto di una trasformata per una costante
$$ \frac{E}{s} = R C \cdot s v_{out}(s) + v_{out}(s) $$
Con qualche passaggio algebrico ottengo l'equazione della tensione in uscita
$$ \frac{E}{s} = v_{out}(s) ( R C s + 1 ) $$
$$ v_{out}(s) = \frac{E}{s( R C s + 1 )} $$
A questo punto, per trovare la soluzione Vout in funzione del tempo calcolo l'anti-trasformata della Vout(s).
$$ L^{-1}[ v_{out}(s) ] = v_{out}(t) $$
$$ L^{-1}[ \frac{E}{s( R C s + 1 )} ] = v_{out}(t) $$
Metto in evidenza RC al denominatore
$$ L^{-1}[ \frac{E}{ R C s^2 + s } ] = v_{out}(t) $$
$$ L^{-1}[ \frac{E}{ R C ( s^2 + \frac{s}{RC} ) } ] = v_{out}(t) $$
$$ L^{-1}[ \frac{E}{ R C } \frac{1}{ s^2 + \frac{s}{RC} } ] = v_{out}(t) $$
$$ L^{-1}[ \frac{E}{ R C } \frac{1}{ s(s+ \frac{1}{RC} ) } ] = v_{out}(t) $$
Per il teorema del prodotto di una trasformata per una costante, faccio uscire il rapporto E/RC
$$ \frac{E}{ R C } L^{-1}[ \frac{1}{ s(s+ \frac{1}{RC} ) } ] = v_{out}(t) $$
In questo modo ho isolato una L-trasformata tipica che posso facilmente trasformare
$$ \frac{E}{ R C } RC (1-e^{-\frac{t}{RC}}) = v_{out}(t) $$
Spiegazione. La trasformata tipica è $$ L[\frac{1}{a}(1-e^{-at})] = \frac{1}{s(s+a)} $$ sostituendo a=(1/RC) ottengo $$ L[\frac{1}{\frac{1}{RC}}(1-e^{-\frac{1}{RC}t})] = \frac{1}{s(s+\frac{1}{RC})} $$
Semplifico e ottengo l'equazione della tensione del condensatore
$$ \frac{E}{ R C } RC (1-e^{-\frac{t}{RC}}) = v_{out}(t) $$
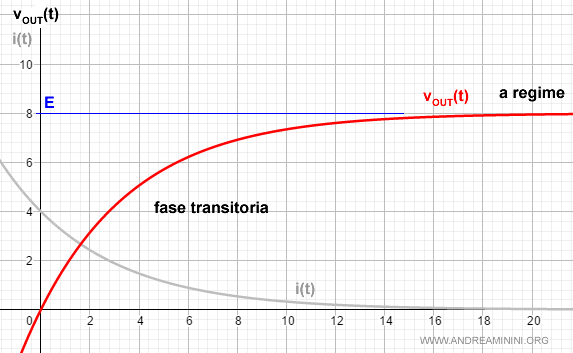
$$ E (1-e^{-\frac{t}{RC}} )= v_{out}(t) $$
Esempio. Se E=8 V, R=2 Ω , C=2 nell'istante t=0 la capacità del condensatore è nulla. L'esponenziale è uguale a 1. Nella fase transitoria il condensatore si carica fino a raggiungere la tensione in uscita pari a 8 volts della fase a regime. Col passare del tempo l'esponenziale tende a zero.
E così via.
