Circuito RL e trasformata di Laplace
Ho un circuito RL composto da un resistore R e una induttanza L.
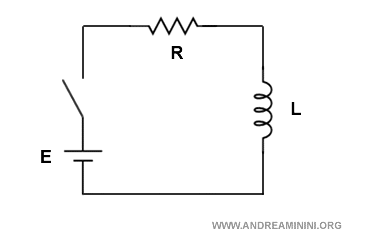
L'interruttore modifica la tensione in ingresso v(t) con un andamento a gradino.
Nell'istante in cui l'interruttore è chiuso la tensione sale a E.

Posso scrivere l'equazione della tensione del circuito nel seguente modo:
$$ v(t) = v_R(t) + v_L(t) $$
Applico la legge di Ohm sulla tensione del resistore
$$ v(t) = R \cdot i(t) + v_L(t) $$
Quindi sostituisco il voltaggio dell'induttore.
$$ v(t) = R \cdot i(t) + L \frac{d \: i(t)}{d \: t} $$
Posso considerare il circuito come un sistema.

La tensione v(t) come il segnale di ingresso del sistema e la corrente i(t) come il segnale di uscita.
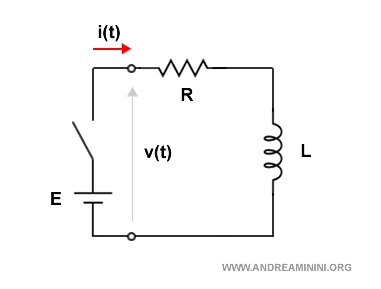
Il segnale di ingresso v(t) varia da 0 a E nell'istante di chiusura dell'interruttore.
Nota. E' la cosiddetta fase transitoria in cui il sistema si adegua alle variazioni del segnale di ingresso.
Il segnale di uscita i(t) è il risultato dell'equazione differenziale.
$$ v(t) = R \cdot i(t) + L \frac{d \: i(t)}{d} $$
Quindi, per determinare l'andamento dell'uscita (corrente) nel tempo devo trovare la soluzione dell'equazione differenziale.
Il che potrebbe diventare molto complesso se il circuito non è semplice.
1] La soluzione tramite la trasformata di Laplace
La trasformata di Laplace mi permette di convertire le equazioni differenziali in equazioni algebriche.
E questo è un bel vantaggio perché le equazioni algebriche sono molto più facili da risolvere.
$$ L [ v(t) ] = V(s) $$
Nota. Per semplicità ipotizzo che l'induttore non abbia energia immagazzinata. Quindi la condizione iniziale del sistema è
$$ i(0)=0 $$
La chiusura dell'interruttore determina un segnale a gradino di ampiezza unitaria pari a E.
La L-trasformata di un gradino unitario è 1/s.
$$ \frac{1}{s} $$
Essendo l'ampiezza pari a E, per il teorema del prodotto della trasformata per una costante ottengo
$$ \frac{1}{s} E $$
Quindi il risultato della trasformata del segnale a gradino di ampiezza unitaria pari a E è
$$ L [ v(t) ] = V(s) = \frac{E}{s} $$
Sostituisco l'equazione differenziale a v(t) nella L-trasformata.
$$ L [ v(t) ] = \frac{E}{s} $$
$$ L [ R \cdot i(t) + L \frac{d \: i(t)}{d} ] = \frac{E}{s} $$
Per il teorema della trasformata di una derivata la L-trasformata a sinistra diventa
$$ R \cdot I(s) + s \cdot L \cdot I(s) = \frac{E}{s} $$
Dove I(s) è la trasformata della corrente L[i(t)]
Con pochi passaggi algebrici ottengo la soluzione della corrente I(s)
$$ I(s) ( R + s \cdot L ) = \frac{E}{s} $$
$$ I(s) = \frac{E}{s( R + s \cdot L )} $$
In questo modo posso calcolare la soluzione del problema per s in modo algebrico.
E' decisamente più semplice da risolvere rispetto a un'equazione differenziale.
2] Il calcolo dell'anti-trasformata
Una volta trovata la soluzione della corrente per I(s), trovo la soluzione i(t) rispetto al tempo tramite l'anti-trasformata.
$$ L^{-1}[I(s)] = i(t) $$
$$ L^{-1}[ \frac{E}{s( R + s \cdot L )} ] = i(t) $$
Il calcolo dell'anti-trasformata non è immediato.
Quindi metto a fattore la variabile se per ricondurla a una forma più facilmente trasformabile.
$$ L^{-1}[ \frac{E}{sR + s^2 L )} ] = i(t) $$
$$ L^{-1}[ \frac{E}{s(R + sL) } ] = i(t) $$
$$ L^{-1}[ \frac{E}{L} \cdot \frac{1}{ s( s+ \frac{R}{L}) } ] = i(t) $$
Poi applico il teorema della combinazione lineare
$$ L^{-1}[ \frac{E}{L} ] \cdot L^{-1}[ \frac{1}{s(s+ \frac{R}{L}) } ] = i(t) $$
Il primo fattore è l'anti-trasformata di una costante. Entrambi i valori E e L sono costati.
E' una L-trasformata tipica. L'anti-trasformata di una costante è la costante stessa.
$$ \frac{E}{L} \cdot L^{-1}[ \frac{1}{s(s+ \frac{R}{L}) } ] = i(t) $$
Spiegazione. L'anti-trasformata del primo fattore è $$ L^{-1}[ \frac{E}{L} ] = \frac{E}{L} $$
Anche l'altra L-trasformata è tipica e si risolve facilmente
$$ \frac{E}{L} \cdot \begin{pmatrix} \frac{1}{\frac{R}{L}}(1-e^{-\frac{R}{L}t}) \end{pmatrix} = i(t) $$
Spiegazione. Una L-trasformata tipica è la seguente: $$ L[\frac{1}{a}(1-e^{-at})] = \frac{1}{s(s+a)} $$ Posso usarla per risolvere questo problema con a=R/L. $$ L[\frac{1}{\frac{R}{L}}(1-e^{-\frac{R}{L}t})] = \frac{1}{s(s+\frac{R}{L})} $$
Semplificando diventa
$$ \frac{E}{L} \cdot \frac{1}{\frac{R}{L}}(1-e^{-\frac{R}{L}t}) = i(t) $$
$$ \frac{E}{L} \cdot \frac{L}{R} \cdot (1-e^{-\frac{R}{L}t}) = i(t) $$
$$ \frac{E}{R} \cdot (1-e^{-\frac{R}{L}t}) = i(t) $$
Ho trovato la soluzione del problema.
Nota. Per t=0 la corrente i(t)=0 perché l'esponenziale è uguale a 1. L'interruttore è aperto e nel circuito non scorre la corrente. Quando chiudo l'interruttore l'esponenziale tende a zero allo scorrere del tempo e la corrente i(t) tende al suo valore di regime E/R. Ad esempio se E=12, R=4, L=2 il valore di regime è E/R=12/3=3 A. Il grafico della funzione i(t) rappresenta perfettamente l'andamento della corrente nel circuito nella fase transitoria (dopo la chiusura del circuito) e nella fase di regime.
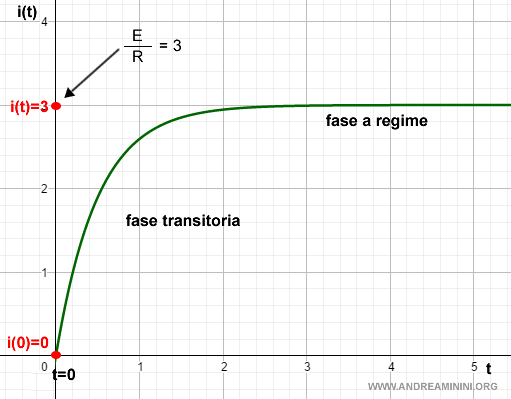
E così via.
