Circuito RC Studio del sistema
Devo studiare la risposta di un circuito RC ossia la tensione Vout.
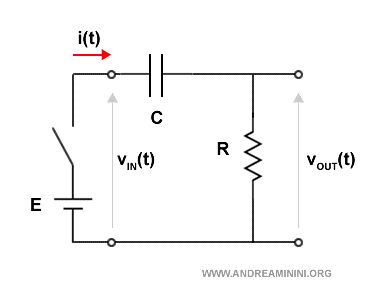
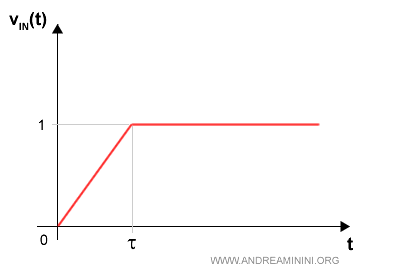
L'interruttore produce un segnale di ingresso a rampa unitaria.
Svolgimento
L'equazione del circuito RC è
$$ v_{in}(t) - v_C(t) - v_R(t) = 0 $$
In questo caso la tensione da studiare è quella del resistore vR=vout.
$$ v_{in}(t) - v_C(t) - v_{out}(t) = 0 $$
$$ v_{in}(t) = v_C(t) + v_{out}(t) $$
Calcolo la trasformata di Laplace delle singole componenti elettroniche
$$ L[v_{in}(t)] = L[v_C(t) + v_{out}(t)] $$
$$ L[v_{in}(t)] = L[v_C(t)] + L[v_{out}(t)] $$
$$ L[v_{in}(t)] = L[v_C(t)] + L[v_{out}(t)] $$
$$ v_{in}(s) = \frac{1}{sC} \cdot I(s) + v_{out}(s) $$
In questo modo ho isolato il ramo del circuito dove si trova resistore, quello su cui devo calcolare la tensione in uscita.
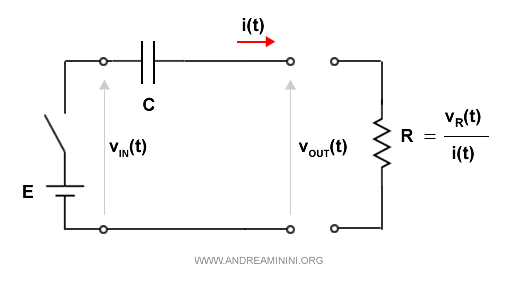
Sapendo che vR = R·i(t) per la legge di Ohm.
$$ v_R = R \cdot i(t) $$
Calcolo la L-trasformata del resistore per ottenere la corrente del circuito.
$$ L[ v_R ] = L[ R \cdot I(t) ] $$
$$ v_R(s) = R \cdot I(s) $$
$$ I(s)= \frac{v_R(s)}{R} $$
Sapendo che VR=Vout
$$ I(s)= \frac{v_{out}(s)}{R} $$
Quindi sostituisco la corrente I(s) all'equazione del circuito.
$$ v_{in}(s) = \frac{1}{sC} \cdot I(s) + v_{out}(s) $$
$$ v_{in}(s) = \frac{1}{sC} \cdot \frac{v_{out}(s)}{R} + v_{out}(s) $$
$$ v_{in}(s) = \frac{v_{out}(s)}{sRC} + v_{out}(s) $$
$$ v_{in}(s) = \frac{v_{out}(s)+v_{out}(s) \cdot sRC}{sRC} $$
$$ v_{in}(s) = \frac{v_{out}(s) \cdot (1+sRC)}{sRC} $$
$$ v_{in}(s) \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
$$ \frac{v_{out}(s)}{v_{in}(s)} = \frac{sRC}{(1+sRC)} $$
Ho ottenuto la funzione di trasferimento del sistema
$$ G(x)=\frac{v_{out}(s)}{v_{in}(s)} $$
Nota. Un sistema generico ha un entrata X e un'uscita Y.
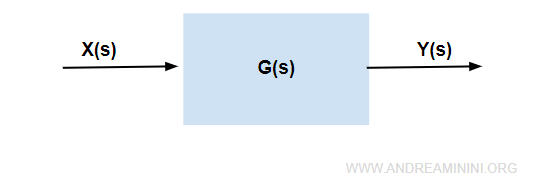
Quindi, sapendo che $$ Y(s) = X(s) \cdot G(s) $$ la funzione di trasferimento del sistema è $$ G(s) = \frac{Y(s)}{X(s)} $$
Sapendo che il segnale di ingresso ha un andamento a rampa unitaria.

Scompongo la funzione nella somma di due funzioni f1 e f2
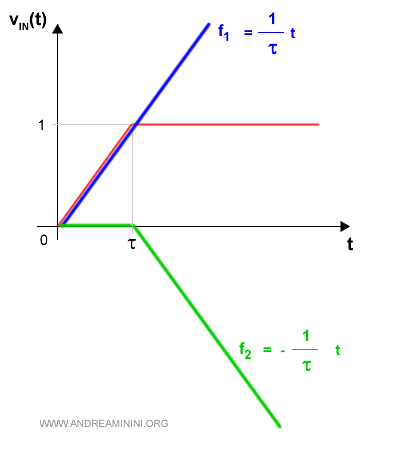
Sapendo che f1+f2 è la somma che determina la funzione del segnale in ingresso vin(t)
$$ L[v_{in}(t)] = L[f_1(t)] + L[f_2(t)] $$
$$ v_{in}(s) = L[f_1(t)] + L[f_2(t)] $$
calcolo separatamente la L-trasformata nell'intervallo da 0 a τ e nell'intervallo da τ in poi
Intervallo da o a τ
Nell'intervallo da 0 a τ la f2 è nulla. Quindi il segnale di ingresso coincide con la f1.
La funzione f1 è una semplice rampa unitaria con pendenza 1/τ
Pertanto, la sua L-trasformata è
$$ L[f_1(t)] = \frac{1}{τs^2} $$
Quindi sapendo che l'equazione trasformata del circuito è
$$ v_{in}(s) \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
Sostituisco vin(s) con la trasformata f1 da 0 a τ
$$ \frac{1}{τs^2} \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
Poi semplifico per cercare di calcolare l'anti-trasformata con una formula tipica
$$ \frac{sRC}{τs^2(1+sRC)} = v_{out}(s) $$
$$ \frac{sRC}{τs^2+τs^3RC} = v_{out}(s) $$
$$ \frac{RC}{τs+τs^2RC} = v_{out}(s) $$
Metto in evidenza le costanti τRC al denominatore
$$ \frac{RC}{ τRC(s^2 + \frac{s}{RC} ) } = v_{out}(s) $$
Poi semplifico
$$ \frac{1}{ τ(s^2 + \frac{s}{RC} ) } = v_{out}(s) $$
$$ \frac{1}{τ} \cdot \frac{1}{ s(s + \frac{1}{RC} ) } = v_{out}(s) $$
Ora posso calcolare l'anti-trasformata
$$ L^{-1} [ \frac{1}{τ} \cdot \frac{1}{ s(s + \frac{1}{RC} ) } ] = L^{-1} [ v_{out}(s) ] $$
$$ L^{-1} [ \frac{1}{τ} ] \cdot L^{-1} [ \frac{1}{ s(s + \frac{1}{RC} ) } ] = v_{out}(t) $$
Per la regola del prodotto di una costante per la trasformata
$$ \frac{1}{τ} \cdot L^{-1} [ \frac{1}{ s(s + \frac{1}{RC} ) } ] = v_{out}(t) $$
L'ultima anti-trasformata è una forma tipica
$$ \frac{1}{τ} \cdot \frac{1}{\frac{1}{RC}} (1-e^{-t \frac{1}{RC} } ) = v_{out}(t) $$
$$ \frac{1}{τ} \cdot RC \cdot (1-e^{ \frac{-t}{RC} } ) = v_{out}(t) $$
$$ \frac{RC}{τ} \cdot (1-e^{ \frac{-t}{RC} } ) = v_{out}(t) $$
Ho trovato l'uscita del circuito da 0 a τ.
Nota. La precedente formula descrive perfettamente l'uscita del circuito vout nell'intervallo da 0 a τ.
Intervallo da τ in poi
Nell'intervallo da τ in poi la L-trasformata del segnale di ingresso è composto dalla somma f1+f2
$$ L[v_{in}(t)] = L[f_1(t)] + L[f_2(t)] $$
$$ v_{in}(s) = L[f_1(t)] + L[f_2(t)] $$
La L-trasformata della funzione f1 è la stessa dell'intervallo da 0 a τ anche nel tratto da τ in poi.
$$ v_{in}(s) = \frac{1}{τs^2} + L[f_2(t)] $$
La funzione f2 è una semplice rampa unitaria con pendenza -1/τ traslata al punto τ
Calcolo la L-trasformata della rampa -1/τ e applico il teorema della traslazione a τ.
$$ v_{in}(s) = \frac{1}{τs^2} - \frac{1}{τs^2} e^{-τs} $$
Nota. La L-trasformata di f2 è $$ L[f_2(t)] = - \frac{1}{τs^2} e^{-τs} $$
$$ v_{in}(s) = \frac{1}{τs^2} ( 1 - e^{-τs} ) $$
Sapendo che l'equazione trasformata del circuito è
$$ v_{in}(s) \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
Sostituisco vin(s) con la trasformata di f1+f2
$$ \frac{1}{τs^2} ( 1 - e^{-τs} ) \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
Poi semplifico e metto in evidenza le costanti per cercare una forma tipica
$$ \frac{1}{τs^2} ( 1 - e^{-τs} ) \cdot \frac{sRC}{(1+sRC)} = v_{out}(s) $$
$$ \frac{1}{τs} ( 1 - e^{-τs} ) \cdot \frac{RC}{(1+sRC)} = v_{out}(s) $$
$$ \frac{1}{τs} ( 1 - e^{-τs} ) \cdot \frac{RC}{RC(\frac{1}{RC}+s)} = v_{out}(s) $$
$$ \frac{1}{τs} ( 1 - e^{-τs} ) \cdot \frac{1}{(\frac{1}{RC}+s)} = v_{out}(s) $$
$$ \frac{1}{τ} ( 1 - e^{-τs} ) \cdot \frac{1}{s(\frac{1}{RC}+s)} = v_{out}(s) $$
$$ \frac{1}{τ} ( \frac{1}{s(\frac{1}{RC}+s)} - \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) = v_{out}(s) $$
Ora posso calcolare l'anti-trasformata
$$ L^{-1}[ \frac{1}{τ} ( \frac{1}{s(\frac{1}{RC}+s)} - \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) ]= L^{-1}[ v_{out}(s) ] $$
$$ L^{-1}[ \frac{1}{τ} ( \frac{1}{s(\frac{1}{RC}+s)} - \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) ]= v_{out}(t) $$
Per la regola del prodotto di una costante per la trasformata
$$ \frac{1}{τ} \cdot L^{-1}[ ( \frac{1}{s(\frac{1}{RC}+s)} - \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) ]= v_{out}(t) $$
$$ L^{-1}[ \frac{1}{τ} ( 1 - e^{-τs} ) \cdot \frac{1}{s(\frac{1}{RC}+s)} ] = L^{-1}[ v_{out}(s) ] $$
$$ \frac{1}{τ} \cdot L^{-1}[ ( \frac{1}{s(\frac{1}{RC}+s)} ] - L^{-1}[ \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) ]= v_{out}(t) $$
La prima L-trasformata inversa è una forma tipica.
$$ \frac{1}{τ} \cdot RC \cdot ( 1 - e^{\frac{-t}{RC}} ) - L^{-1}[ \frac{1}{s(\frac{1}{RC}+s)} e^{-τs} ) ]= v_{out}(t) $$
La seconda e ultima L-trasformata inversa è una forma tipica a cui è applicato il teorema della traslazione.
$$ \frac{1}{τ} \cdot RC \cdot ( 1 - e^{\frac{-t}{RC}} ) - RC \cdot ( 1 - e^{ - \frac{t-τ}{RC}} ) = v_{out}(t) $$
Dopo qualche passaggio algebrico ottengo l'equazione della risposta del sistema rispetto al tempo nell'intervallo da τ in poi.
$$ \frac{1}{τ} \cdot RC \cdot ( 1 - e^{\frac{-t}{RC}} - 1 + e^{ - \frac{t-τ}{RC}} ) = v_{out}(t) $$
$$ \frac{RC}{τ} \cdot ( - e^{\frac{-t}{RC}} + e^{- \frac{t-τ}{RC}} ) = v_{out}(t) $$
E così via.
