Le misure ripetute

Una misura ripetuta consiste nel rilevare più volte la stessa grandezza per ottenere un risultato più affidabile e ridurre l’effetto degli errori casuali.

Prendendo la media delle misure ripetute, ottengo una stima più accurata del valore reale della grandezza che voglio misurare.

L’intervallo di variazione tra le misure mi aiuta anche a quantificare l’incertezza associata alla misurazione e riduce l'impatto degli errori casuali.

In altre parole, spesso si ripete la stessa misurazione più volte al solo scopo di ridurre l’incertezza e ottenere una stima più accurata del valore vero di una grandezza. In molti casi, infatti, più che aumentare il numero di cifre significative di una singola misura, è meglio ripeterla più volte per ottenere un risultato più affidabile.

Perché fare misure ripetute?

Le misure singole possono essere soggette a vari tipi di errori, tra cui:

• Errori casuali
  Sono delle variazioni imprevedibili dovute a piccoli cambiamenti ambientali, errori di lettura o oscillazioni dello strumento. Questi errori tendono a influenzare ogni misurazione in modo diverso, causando piccole fluttuazioni nei risultati.
• Errori sistematici
  Sono errori costanti che possono derivare da un'impostazione non corretta dello strumento o da una tecnica di misurazione sbagliata. Questi errori non vengono ridotti dalle misure ripetute, ma posso individuarli confrontando le misure con valori noti o con strumenti diversi.

Le misure ripetute aiutano soprattutto a ridurre l’effetto degli errori casuali.

Tuttavia, utilizzando strumenti di misura diversi, le misure ripetute mi permettono anche rilevare eventuali errori sistematici, ossia valori anomali causati da uno strumento.

In generale, prendendo la media di più misurazioni, si ottiene una stima più affidabile del valore vero della grandezza, mentre l’intervallo di variazione delle misure fornisce informazioni sulla precisione.

Anche pochi valori aggiuntivi possono fornire una visione più chiara della precisione di una misura.

Come trattare le misure ripetute: media e errore

Quando dispongo di una serie di misurazioni della stessa grandezza, ad esempio \( x_1, x_2, \ldots, x_n \), posso calcolare:

• La media aritmetica dei valori rilevati
  La media aritmetica dei valori rilevati rappresenta una stima più attendibile del valore vero della grandezza \( X \) misurata rispetto alle singole rilevazioni. $$ X = \frac{x_1 + x_2 + \dots + x_n}{n} $$
• Errore assoluto
  Per stimare l'errore assoluto calcolo la metà della differenza tra la misura massima \( x_{\text{max}} \) e la misura minima \( x_{\text{min}} \) dei valori rilevati. Questo metodo è molto utile per stimare l'incertezza quando ci sono poche misure. $$ \Delta X = \frac{x_{\text{max}} - x_{\text{min}}}{2} $$

  Nota.  In presenza di un numero significativo di misure, è preferibile calcolare la deviazione standard perché fornisce una stima più rigorosa dell’incertezza. La deviazione standard misura della dispersione delle misure attorno alla media.

Un esempio pratico

In questo esempio misuro più volte il diametro di una sfera usando un metro graduato in millimetri, ottenendo i seguenti valori (in cm):

$$ 10.1 , 10.2 ,  10.0,  10.3, 10.1 $$

Calcolo la media aritmetica dei valori rilevati.

$$ X = \frac{10.1 + 10.2 + 10.0 + 10.3 + 10.1}{5} = \frac{50.7}{5} = 10.14 \ \text{cm} $$

Quindi, la stima del valore medio è $ X = 10.14 \ \text{cm} $

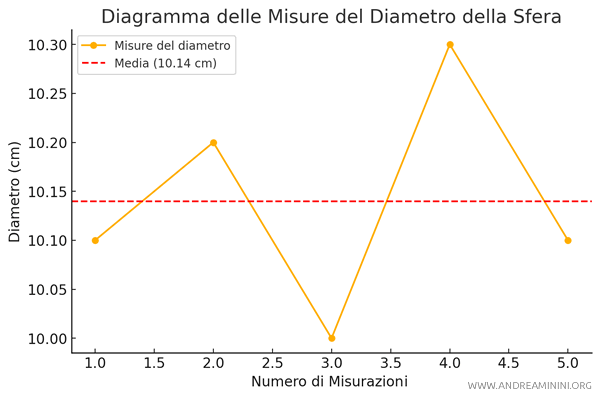
Per calcolare l'errore assoluto, trovo i valori massimo e minimo nella serie delle rilevazioni:

$$ x_{\text{max}} = 10.3 $$

$$  x_{\text{min}} = 10.0 $$

Poi calcolo la media aritmetica tra questi due valori:

$$ \Delta X = \frac{10.3 - 10.0}{2} = \frac{0.3}{2} = 0.15 \ \text{cm} $$

Quindi, l'errore assoluto è $ 0.15 \ \text{cm} $

In conclusione, la misura finale del diametro posso esprimerla come:

$$ X = 10.14 \pm 0.15 \ \text{cm} $$

La media di misure ripetute riduce l'incidenza degli errori casuali e migliora la precisione del risultato.

E così via.