La differenza tra arrotondamento e troncamento

L’approssimazione per troncamento si ottiene eliminando le cifre decimali oltre un certo limite. L’approssimazione per arrotondamento, invece, sceglie il numero più vicino al valore originale, aumentando l’ultima cifra conservata se la prima eliminata è maggiore o uguale a 5.

L'approssimazione di un numero reale \( r \) è una pratica comune in matematica e nelle scienze per gestire numeri con molte cifre decimali, soprattutto quando la precisione è limitata dagli strumenti di misurazione.

Inoltre, alcuni numeri reali sono irrazionali, ad esempio il pi greco \( \pi = 3,1415926... \) o la radice quadrata di due \( \sqrt{2}=1,41421... \), il che significa che hanno una parte decimale infinita e non periodica.

In questi casi, l'approssimazione diventa indispensabile per poter rappresentare e utilizzare questi numeri nei calcoli matematici, mantenendo un livello di precisione adeguato.

Approssimazione per troncamento e arrotondamento

Due metodi per approssimare un numero reale sono il troncamento e l'arrotondamento.

• Troncamento
  Il troncamento è la riduzione del numero a un certo numero di cifre decimali senza modificarle, eliminando semplicemente le cifre successive. Questo metodo è utilizzato quando è necessario un'approssimazione per difetto, ossia inferiore al valore reale.

  Esempio. L'approssimazione per troncamento di \( \pi = 3,1415926... \) alla terza cifra decimale è \( \pi \approx 3,141 \).

• Arrotondamento
  L'approssimazione per arrotondamento avviene scegliendo, tra i valori con un certo numero di cifre decimali, quello più vicino al valore reale di \( r \). Per determinare se arrotondare per eccesso o per difetto, guardo il valore della prima cifra decimale che sto eliminando:
  • Se la cifra omessa è minore di 5, il numero arrotondato coincide con quello troncato.
  • Se la cifra omessa è maggiore o uguale a 5, aumento di un'unità l'ultima cifra decimale conservata.

  Esempio. L'arrotondamento di \( \pi = 3,1415926... \) alla terza cifra decimale è \( \pi \approx 3,142 \) perché la prima cifra omessa è 5 ( ossia \( \pi = 3,141\color{red}{5}926... \) ) quindi l'arrotondamento diventa \( 3,142 \). In questo caso l'approssimazione è per eccesso.
  

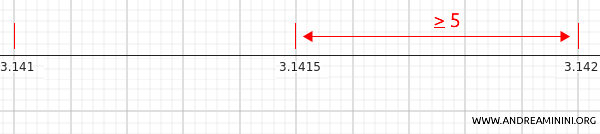
  Nota. In questo caso particolare sottolineo che i numeri più vicini \( 3,141 \) e \( 3,42 \) sono equidistanti da \( 3,1415 \) ma per convenzione se l'ultima cifra omessa è maggiore o uguale a 5 si sceglie comunque quello superiore ovvero \( 3,142 \).

  Viceversa, l'arrotondamento di \( \pi = 3,1415926... \) alla seconda cifra decimale è \( \pi \approx 3,14 \) perché la prima cifra omessa è 1 ( ossia \( \pi = 3,14\color{red}{1}5926... \) ) ed è minore di 5, quindi l'arrotondamento diventa conservativo \( 3,14 \). In questo caso l'approssimazione è per difetto.
  
  E' evidente che il numero \( 3.141 \) è molto più vicino a \( 3.14 \) rispetto a \( 3.15 \).

Queste regole di troncamento e arrotondamento mi consentono di gestire i numeri in modo preciso e pratico, mantenendo il controllo sull’accuratezza dei risultati.

Differenze tra troncamento e arrotondamento

In generale, il troncamento porta sempre a un’approssimazione per difetto, mai superiore al numero reale.

L'arrotondamento, invece, è un'approssimazione per difetto se la prima cifra omessa è minore di 5 oppure o per eccesso se la cifra omessa è 5 o superiore.

Nota. La scelta tra troncamento e arrotondamento si basa sulle esigenze specifiche di precisione e accuratezza del calcolo e sul contesto. In ambiti dove è richiesta una stima conservativa o inferiore, preferisco il troncamento, mentre l'arrotondamento è la scelta migliore quando voglio ottenere un'approssimazione più vicina al valore reale.

Pro e contro del troncamento e dell'arrotondamento

Entrame le tecniche di approssimazione hanno vantaggi e svantaggi:

Troncamento

• Pro. Il troncamento è un metodo veloce e semplice da applicare, poiché basta eliminare le cifre oltre un certo limite senza ulteriori calcoli. Mantiene il valore finale sempre inferiore o uguale al numero originale. Quindi, è utile in contesti dove serve una “stima conservativa” (approssimazione per difetto).
• Contro. Il principale contro è la minor precisione. Tagliando semplicemente le cifre decimali, il valore può risultare meno accurato rispetto all’originale, soprattutto se le cifre tagliate sono vicine a metà. Inoltre, si presta maggiormente al rischio dell'accumulo e alla propagazione di un errore. Ad esempio, in calcoli ripetuti, come nelle somme di valori troncati, l’errore può accumularsi e portare a una stima finale imprecisa.

Arrotondamento

• Pro. Uno dei vantaggi dell'arrotondamento è la maggiore accuratezza, poiché si sceglie il valore più vicino, l’arrotondamento. Quindi, l'arrotondamento tende a preservare una maggiore precisione rispetto all’originale. Questo significa che negli aggregati o nei calcoli ripetuti l’arrotondamento bilancia gli errori in eccesso o difetto, minimizzando gli scostamenti complessivi.
• Contro. Il procedimento di calcolo è più complesso perché richiede un passaggio in più per verificare la cifra eliminata e decidere se aumentare l’ultima cifra conservata. L’arrotondamento può portare a un valore finale leggermente superiore all’originale, il che può influire in contesti in cui è importante non superare il valore reale (es. calcolo della distanza percorribile con il carburante nel serbatoio di un aereo).

E così via.