Esercizi sulla notazione scientifica
Converti \( 4,5 \cdot 10^3 \, \text{kg} \) in grammi:
Per convertire \( 4,5 \cdot 10^3 \, \text{kg} \) in grammi, posso usare la conversione che prevede di moltiplicare per \( 10^3 \) (poiché ci sono tre spostamenti della virgola verso destra):
$$ 4,5 \cdot 10^3 \, \text{kg} $$
$$ 4,5 \cdot 10^3 \times 10^3 \, \text{g} $$
$$ 4,5 \cdot 10^{3+3} \, \text{g} $$
$$ 4,5 \cdot 10^6 \, \text{g} $$
Quindi, \( 4,5 \cdot 10^3 \, \text{kg} \) è equivalente a \( 4,5 \cdot 10^6 \, \text{g} \).
Metodo di risoluzione. Questo problema può essere risolto a mente contando gli spostamenti della virgola verso destra o verso sinistra per passare da un multiplo all'altro e moltiplicare o dividere in base 10 per le relative posizioni.
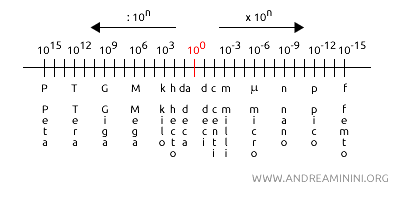
In questo caso per passare da 103 (k) a 100=1 ci sono tre spostamenti della virgola verso destra, quindi devo moltiplicare per 103.
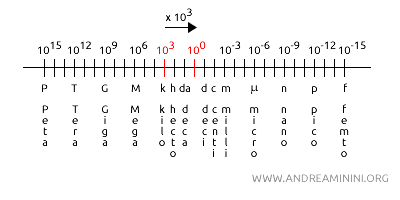
In alternativa, posso risolverlo scrivendo un'equivalenza come la seguente: $$ 4,5 \cdot 10^3 \, \text{kg} = x \ \text{g} $$ Sostituisco k con la potenza 103. $$ 4,5 \cdot 10^3 \cdot 10^3 \ \text{g} = x \ \text{g} $$ $$ 4,5 \cdot 10^6 \ \text{g} = x \ \text{g} $$ Poi ricavo x $$ x = \frac{4,5 \cdot 10^6 \ \text{g} }{g} $$ $$ x = 4,5 \cdot 10^6 $$ Quindi, sostituisco x nell'equivalenza iniziale $$ 4,5 \cdot 10^3 \, \text{kg} = x \ \text{g} $$ $$ 4,5 \cdot 10^3 \, \text{kg} = 4,5 \cdot 10^6 \ \text{g} $$
Converti \( 2,0 \cdot 10^2 \, \text{g} \) in chilogrammi:
Per convertire \( 2,0 \cdot 10^2 \, \text{g} \) in chilogrammi, devo dividere per \( 10^3 \) (poiché ci sono tre spostamenti della virgola verso sinistra):
$$ 2,0 \cdot 10^2 \, \text{g} $$
$$ 2,0 \cdot 10^2 \div 10^3 \, \text{kg} $$
$$ 2,0 \cdot 10^{2-3} \, \text{kg} $$
$$ 2,0 \cdot 10^{-1} \, \text{kg} $$
Quindi, \( 2,0 \cdot 10^2 \, \text{g} \) è equivalente a \( 2,0 \cdot 10^{-1} \, \text{kg} \)
Procedimento. Scrivo l'equivalenza $$ 2,0 \cdot 10^2 \, \text{g} = x \ \text{kg} $$ Sostituisco il multiplo k sapendo che $ 1 k = 10^3 $ $$ 2,0 \cdot 10^2 \, \text{g} = x \cdot 10^3 \ \text{g} $$ Ricavo x $$ x = \frac{2,0 \cdot 10^2 \, \text{g} }{ 10^3 \ \text{g}} $$ $$ x = \frac{2,0 \cdot 10^2 }{ 10^3 } $$ $$ x = 2,0 \cdot 10^{2-3} $$ $$ x = 2,0 \cdot 10^{-1} $$ Una volta trovato il valore della variabile x=2·10-1, lo sostituisco nell'equivalenza iniziale. $$ 2,0 \cdot 10^2 \, \text{g} = x \ \text{kg} $$ $$ 2,0 \cdot 10^2 \, \text{g} = 2,0 \cdot 10^{-1} \ \text{kg} $$
Converti \( 9,0 \cdot 10^5 \, \text{g} \) in chilogrammi:
Per convertire \( 9,0 \cdot 10^5 \, \text{g} \) in chilogrammi, divido per \( 10^3 \). Questo significa che sposto la virgola 3 posizioni a sinistra.
Quindi, ho:
\[
9,0 \cdot 10^5 \, \text{g} = \frac{9,0 \cdot 10^5}{10^3} \, \text{kg} = 9,0 \cdot 10^{5-3} \, \text{kg} = 9,0 \cdot 10^2 \, \text{kg}
\]
Pertanto, \( 9,0 \cdot 10^5 \, \text{g} \) è equivalente a \( 9,0 \cdot 10^2 \, \text{kg} \) o \( 900 \, \text{kg} \)
Converti \( 3,2 \cdot 10^{-3} \, \text{s} \) in microsecondi:
Per convertire \( 3,2 \cdot 10^{-3} \, \text{s} \) in microsecondi, moltiplico per \( 10^6 \) (poiché 1 secondo è equivalente a \( 10^6 \) microsecondi). Questo significa che sposto la virgola 6 posizioni a destra.
Quindi, ho:
$$ 3,2 \cdot 10^{-3} \, \text{s} = 3,2 \cdot 10^{-3} \times 10^6 \, \mu\text{s} = 3,2 \cdot 10^{6-3} \, \mu\text{s} = 3,2 \cdot 10^3 \, \mu\text{s} $$
Pertanto, \( 3,2 \cdot 10^{-3} \, \text{s} \) è equivalente a \( 3,2 \cdot 10^3 \, \mu\text{s} \) o \( 3200 \, \mu\text{s} \).
Converti \( 1,1 \cdot 10^2 \, \text{kg} \) in grammi:
Per convertire \( 1,1 \cdot 10^2 \, \text{kg} \) in grammi, moltiplico per \( 10^3 \) (poiché 1 kg è equivalente a 1000 grammi). Questo significa che sposto la virgola 3 posizioni a destra.
Quindi, ho:
\[
1,1 \cdot 10^2 \, \text{kg} = 1,1 \cdot 10^2 \times 10^3 \, \text{g} = 1,1 \cdot 10^{2+3} \, \text{g} = 1,1 \cdot 10^5 \, \text{g}
\]
Pertanto, \( 1,1 \cdot 10^2 \, \text{kg} \) è equivalente a \( 1,1 \cdot 10^5 \, \text{g} \) o \( 110000 \, \text{g} \).
Converti \( 6,5 \cdot 10^{-2} \, \text{s} \) in millisecondi:
Per convertire \( 6,5 \cdot 10^{-2} \, \text{s} \) in millisecondi, moltiplico per \( 10^3 \) (poiché 1 secondo è equivalente a 1000 millisecondi). Questo significa che sposto la virgola 3 posizioni a destra.
Quindi, ho:
\[
6,5 \cdot 10^{-2} \, \text{s} = 6,5 \cdot 10^{-2} \times 10^3 \, \text{ms} = 6,5 \cdot 10^{3-2} \, \text{ms} = 6,5 \cdot 10^1 \, \text{ms}
\]
Pertanto, \( 6,5 \cdot 10^{-2} \, \text{s} \) è equivalente a \( 6,5 \cdot 10^1 \, \text{ms} \) o \( 65 \, \text{ms} \).
Converti \( 4,2 \cdot 10^6 \, \text{g} \) in chilogrammi:
Per convertire \( 4,2 \cdot 10^6 \, \text{g} \) in chilogrammi, divido per \( 10^3 \) (poiché 1 chilogrammo è equivalente a 1000 grammi). Questo significa che sposto la virgola 3 posizioni a sinistra.
Quindi, ho:
\[
4,2 \cdot 10^6 \, \text{g} = \frac{4,2 \cdot 10^6}{10^3} \, \text{kg} = 4,2 \cdot 10^{6-3} \, \text{kg} = 4,2 \cdot 10^3 \, \text{kg}
\]
Pertanto, \( 4,2 \cdot 10^6 \, \text{g} \) è equivalente a \( 4,2 \cdot 10^3 \, \text{kg} \) o \( 4200 \, \text{kg} \).
Converti \( 5,2 \cdot 10^2 \, \text{mg} \) in grammi:
Per convertire \( 5,2 \cdot 10^2 \, \text{mg} \) in grammi, divido per \( 10^3 \) (poiché 1 grammo è equivalente a 1000 milligrammi). Questo significa che sposto la virgola 3 posizioni a sinistra.
Quindi, ho:
\[
5,2 \cdot 10^2 \, \text{mg} = \frac{5,2 \cdot 10^2}{10^3} \, \text{g} = 5,2 \cdot 10^{2-3} \, \text{g} = 5,2 \cdot 10^{-1} \, \text{g}
\]
Pertanto, \( 5,2 \cdot 10^2 \, \text{mg} \) è equivalente a \( 5,2 \cdot 10^{-1} \, \text{g} \) o \( 0,52 \, \text{g} \).
Converti \( 7,1 \cdot 10^5 \, \text{cm} \) in chilometri:
Per convertire \( 7,1 \cdot 10^5 \, \text{cm} \) in chilometri, divido per \( 10^5 \) (poiché 1 chilometro è equivalente a \( 100000 \) centimetri, ovvero \( 10^5 \) cm). Questo significa che sposto la virgola 5 posizioni a sinistra.
Quindi, ho:
\[
7,1 \cdot 10^5 \, \text{cm} = \frac{7,1 \cdot 10^5}{10^5} \, \text{km} = 7,1 \cdot 10^{5-5} \, \text{km} = 7,1 \cdot 10^0 \, \text{km}
\]
Pertanto, \( 7,1 \cdot 10^5 \, \text{cm} \) è equivalente a \( 7,1 \, \text{km} \).
Converti \( 8,9 \cdot 10^7 \, \text{μm} \) in metri:
Per convertire \( 8,9 \cdot 10^7 \, \mu\text{m} \) in metri, divido per \( 10^6 \) (poiché 1 metro è equivalente a \( 1.000.000 \) micrometri, ovvero \( 10^6 \) μm). Questo significa che sposto la virgola 6 posizioni a sinistra.
Quindi, ho:
\[
8,9 \cdot 10^7 \, \mu\text{m} = \frac{8,9 \cdot 10^7}{10^6} \, \text{m} = 8,9 \cdot 10^{7-6} \, \text{m} = 8,9 \cdot 10^1 \, \text{m}
\]
Pertanto, \( 8,9 \cdot 10^7 \, \mu\text{m} \) è equivalente a \( 8,9 \cdot 10^1 \, \text{m} \) o \( 89 \, \text{m} \).
Converti \( 2,5 \cdot 10^{-2} \, \text{s} \) in nanosecondi:
Per convertire \( 2,5 \cdot 10^{-2} \, \text{s} \) in nanosecondi, moltiplico per \( 10^9 \) (poiché 1 secondo è equivalente a \( 1.000.000.000 \) nanosecondi, ovvero \( 10^9 \) ns). Questo significa che sposto la virgola 9 posizioni a destra.
Quindi, ho:
\[
2,5 \cdot 10^{-2} \, \text{s} = 2,5 \cdot 10^{-2} \times 10^9 \, \text{ns} = 2,5 \cdot 10^{9-2} \, \text{ns} = 2,5 \cdot 10^7 \, \text{ns}
\]
Pertanto, \( 2,5 \cdot 10^{-2} \, \text{s} \) è equivalente a \( 2,5 \cdot 10^7 \, \text{ns} \) o \( 25000000 \, \text{ns} \).
Converti \( 1,5 \cdot 10^9 \, \text{bytes} \) in gigabytes:
Per convertire \( 1,5 \cdot 10^9 \, \text{bytes} \) in gigabytes, divido per \( 10^9 \) (poiché 1 gigabyte è equivalente a \( 1.000.000.000 \) bytes, ovvero \( 10^9 \) bytes). Questo significa che sposto la virgola 9 posizioni a sinistra.
Quindi, ho:
\[
1,5 \cdot 10^9 \, \text{bytes} = \frac{1,5 \cdot 10^9}{10^9} \, \text{GB} = 1,5 \cdot 10^{9-9} \, \text{GB} = 1,5 \cdot 10^0 \, \text{GB}
\]
Pertanto, \( 1,5 \cdot 10^9 \, \text{bytes} \) è equivalente a \( 1,5 \, \text{GB} \).
Converti \( 4,2 \cdot 10^5 \, \text{nanometri (nm)} \) in millimetri (mm):
Per convertire \( 4,2 \cdot 10^5 \, \text{nm} \) in millimetri, devo tenere presente che 1 millimetro è equivalente a \( 1.000.000 \) nanometri, ovvero \( 10^6 \) nm.
Pertanto, divido per \( 10^6 \) (questo significa che sposto la virgola 6 posizioni a sinistra).
Quindi, ho:
\[
4,2 \cdot 10^5 \, \text{nm} = \frac{4,2 \cdot 10^5}{10^6} \, \text{mm} = 4,2 \cdot 10^{5-6} \, \text{mm} = 4,2 \cdot 10^{-1} \, \text{mm}
\]
Pertanto, \( 4,2 \cdot 10^5 \, \text{nm} \) è equivalente a \( 4,2 \cdot 10^{-1} \, \text{mm} \) o \( 0,42 \, \text{mm} \).
Procedimento. In questo caso per scrivere l'equivalenza devo considerare i simboli di entrambi i multipli. $$ 4,2 \cdot 10^5 \, \text{nm} = x \ \text{mm}$$ Dove 1 n = 10-9 e 1m=10-3. $$ 4,2 \cdot 10^5 \cdot 10^{-9} \text{m} = x \cdot 10^{-3} \ \text{m}$$ $$ 4,2 \cdot 10^{-4} \text{m} = x \cdot 10^{-3} \ \text{m}$$ $$ x = \frac{ 4,2 \cdot 10^{-4} \text{m} }{ 10^{-3} \ \text{m} }$$ $$ x = \frac{ 4,2 \cdot 10^{-4} }{ 10^{-3} \ }$$ $$ x = 4,2 \cdot 10^{-4-(-3)} $$ $$ x = 4,2 \cdot 10^{-4+3} $$ $$ x = 4,2 \cdot 10^{-1} $$ Una volta trovato il valore di x=4,2·10-1 posso completare l'equivalenza iniziale. $$ 4,2 \cdot 10^5 \, \text{nm} = x \ \text{mm}$$ $$ 4,2 \cdot 10^5 \, \text{nm} = 4,2 \cdot 10^{-1} \ \text{mm}$$
Converti \( 3,6 \cdot 10^8 \, \text{gigawatt (GW)} \) in decawatt (daW):
Per convertire \( 3,6 \cdot 10^8 \, \text{GW} \) in decawatt (daW), devo considerare che ci sono 8 posizioni da gigawatt a watt e 1 posizione da watt a decawatt. In totale, ci sono 9 spostamenti.
Quindi, ho:
\[
3,6 \cdot 10^8 \, \text{GW} = 3,6 \cdot 10^{8 + 9} \, \text{daW} = 3,6 \cdot 10^{17} \, \text{daW}
\]
Pertanto, \( 3,6 \cdot 10^8 \, \text{GW} \) è equivalente a \( 3,6 \cdot 10^{17} \, \text{daW} \).
Converti \( 2,5 \cdot 10^3 \, \text{kilogrammi (kg)} \) in milligrammi (mg):
Per convertire \( 2,5 \cdot 10^3 \, \text{kg} \) in milligrammi (mg), conto le posizioni da chilogrammi a milligrammi.
Ci sono 3 posizioni da chilogrammi a grammi (1 kg = \( 10^3 \) g) e altre 3 posizioni da grammi a milligrammi (1 g = \( 10^3 \) mg).
In totale, ci sono 6 spostamenti.
Quindi, ho:
$$ 2,5 \cdot 10^3 \, \text{kg} = 2,5 \cdot 10^{3 + 6} \, \text{mg} = 2,5 \cdot 10^9 \, \text{mg} $$
Pertanto, \( 2,5 \cdot 10^3 \, \text{kg} \) è equivalente a \( 2,5 \cdot 10^9 \, \text{mg} \).
Converti \( 7,1 \cdot 10^2 \, \text{picosecondi (ps)} \) in nanosecondi (ns):
Per convertire \( 7,1 \cdot 10^2 \, \text{ps} \) in nanosecondi (ns), conto le posizioni da picosecondi a nanosecondi.
In totale, ci sono 6 spostamenti da picosecondi a nanosecondi.
Quindi, ho:
$$ 7,1 \cdot 10^2 \, \text{ps} = 7,1 \cdot 10^{2 - 6} \, \text{ns} = 7,1 \cdot 10^{-4} \, \text{ns} $$
Pertanto, \( 7,1 \cdot 10^2 \, \text{ps} \) è equivalente a \( 7,1 \cdot 10^{-4} \, \text{ns} \).
Converti \( 9,5 \cdot 10^{-3} \, \text{terametri (Tm)} \) in megametri (Mm):
Per convertire \( 9,5 \cdot 10^{-3} \, \text{Tm} \) in megametri (Mm), conto le posizioni da terametri a megametri.
Ci sono 6 posizioni da terametri a metri (1 Tm = \( 10^{12} \) m, 1 Mm = \( 10^6 \) m) e altre 6 posizioni da metri a megametri.
In totale, ci sono 12 spostamenti da terametri a megametri.
Quindi, ho:
$$ 9,5 \cdot 10^{-3} \, \text{Tm} = 9,5 \cdot 10^{-3 + 12} \, \text{Mm} = 9,5 \cdot 10^9 \, \text{Mm} $$
Pertanto, \( 9,5 \cdot 10^{-3} \, \text{Tm} \) è equivalente a \( 9,5 \cdot 10^9 \, \text{Mm} \).
Converti \( 8,3 \cdot 10^4 \, \text{megabyte (MB)} \) in kilobyte (KB):
Per convertire \( 8,3 \cdot 10^4 \, \text{MB} \) in kilobyte (KB), conto le posizioni da megabyte a kilobyte.
Ci sono 2 posizioni da megabyte a kilobyte (1 MB = \( 10^6 \) bytes e 1 KB = \( 10^3 \) bytes).
In totale, ci sono 2 spostamenti da megabyte a kilobyte.
Quindi, ho:
$$ 8,3 \cdot 10^4 \, \text{MB} = 8,3 \cdot 10^{4 + 2} \, \text{KB} = 8,3 \cdot 10^6 \, \text{KB} $$
Pertanto, \( 8,3 \cdot 10^4 \, \text{MB} \) è equivalente a \( 8,3 \cdot 10^6 \, \text{KB} \).
Converti \( 6,4 \cdot 10^{-2} \, \text{petametri (Pm)} \) in terametri (Tm):
Per convertire \( 6,4 \cdot 10^{-2} \, \text{Pm} \) in terametri (Tm), conto le posizioni da petametri a terametri.
Ci sono 3 posizioni da petametri a terametri (1 Pm = \( 10^{15} \) m e 1 Tm = \( 10^{12} \) m).
In totale, ci sono 3 spostamenti da petametri a terametri.Quindi, ho:
$$ 6,4 \cdot 10^{-2} \, \text{Pm} = 6,4 \cdot 10^{-2 + 3} \, \text{Tm} = 6,4 \cdot 10^{1} \, \text{Tm} $$
Pertanto, \( 6,4 \cdot 10^{-2} \, \text{Pm} \) è equivalente a \( 6,4 \cdot 10 \ \text{Tm} \).
Procedimento. Il problema si può risolvere anche con un'equivalenza.$$ 6.4 \cdot 10^{-2} Pm = x \ Tm $$ Da cui ricavo la variabile x. $$ x = \frac{6.4 \cdot 10^{-2} Pm}{Tm} $$ $$ x = \frac{6.4 \cdot 10^{-2} P}{T} $$ Sapendo che $ 1 P = 10^{15} $ e $ 1 T = 10^{12} $ $$ x = \frac{6.4 \cdot 10^{-2} \cdot 10^{15}}{10^{12}} $$ $$ x = \frac{6.4 \cdot 10^{-2+15}}{10^{12}} $$ $$ x = \frac{6.4 \cdot 10^{13}}{10^{12}} $$ $$ x = 6.4 \cdot 10^{13-12} $$ $$ x = 6.4 \cdot 10^{1} $$ Quindi $ x = 6.4 \cdot 10 $ $$ 6.4 \cdot 10^{-2} Pm = x \ Tm $$ $$ 6.4 \cdot 10^{-2} Pm = 6.4 \cdot 10 \ Tm $$
Converti \( 1,2 \cdot 10^{-8} \, \text{hectogrammi (hg)} \) in decagrammi (dag):
Per convertire \( 1,2 \cdot 10^{-8} \, \text{hg} \) in decagrammi (dag), conto le posizioni da hectogrammi a decagrammi.
Ci sono 2 posizioni da hectogrammi a decagrammi (1 hg = \( 10^2 \) g e 1 dag = \( 10 \) g).
Quindi, ho:
$$ 1,2 \cdot 10^{-8} \, \text{hg} = 1,2 \cdot 10^{-8 + 2} \, \text{dag} = 1,2 \cdot 10^{-6} \, \text{dag} $$
Pertanto, \( 1,2 \cdot 10^{-8} \, \text{hg} \) è equivalente a \( 1,2 \cdot 10^{-6} \, \text{dag} \).
