Errori di misurazione

Gli errori di misurazione sono delle discrepanze tra il valore osservato durante una misurazione e il valore reale della grandezza che sto misurando.

Queste discrepanze sono generate da limiti o difetti intrinseci degli strumenti oppure dalla procedura di misurazione che sto utilizzando.

Sono sempre presenti in qualsiasi misurazione, dalla semplice misurazione della temperatura fino a calcoli complessi nelle scienze sperimentali.

Gli errori di misura sono una componente inevitabile di ogni misurazione scientifica, ma con una gestione attenta è possibile ridurli significativamente. Ad esempio, gli errori sistematici richiedono interventi sugli strumenti o sui metodi, mentre gli errori accidentali si riducono aumentando il numero di osservazioni. In questo modo, posso ottenere un risultato più vicino alla realtà.

Tipi di errori di misura

Gli errori di misura si suddividono principalmente in errori sistematici ed errori accidentali.

A] Errori Sistematici

Gli errori sistematici sono quelli causati da problemi nel metodo di misurazione o nello strumento stesso.

Quindi, si ripetono costantemente nello stesso senso, cioè o sempre per eccesso o sempre per difetto, ogni volta che effettuo la misurazione.

Ad esempio, se uno strumento ha un difetto di taratura o se è influenzato da fattori ambientali, tenderà a dare sempre un risultato spostato rispetto al valore reale. Questo tipo di errore non si annulla con la ripetizione delle misurazioni, poiché ha una causa definita e costante.

Gli errori sistematici di misura rappresentano, a mio avviso, una sorta di "illusione di precisione": sono insidiosi proprio perché tendono a ripetersi in modo coerente, dando l’apparenza di una misurazione affidabile quando in realtà l’intero sistema di misura è difettoso.

Quali sono le tecniche per gestire gli errori sistematici?

Per limitare l'effetto degli errori sistematici, devo calibrare regolarmente gli strumenti, verificarne il corretto funzionamento, e in alcuni casi, utilizzare diversi strumenti per la stessa misurazione.

Una tecnica efficace è il confronto dei risultati ottenuti da diversi strumenti o metodi, oppure il confronto con dei dati già noti e sicuri, in modo da identificare eventuali discrepanze sistematiche.

B] Errori casuali o accidentali

Gli errori casuali sono provocati da variabili imprevedibili e occasionali, come lievi variazioni ambientali o piccole fluttuazioni nei metodi di esecuzione della misura.

A differenza degli errori sistematici, gli errori accidentali possono variare in entrambi i sensi (per eccesso e per difetto) e generalmente seguono una distribuzione casuale.

Ad esempio, nel misurare la durata di un battito cardiaco con un cronometro, anche il più piccolo ritardo nel premere il pulsante può influenzare il risultato, introducendo una variazione casuale in ogni rilevazione. Lo stesso vale per la misurazione della lunghezza di un oggetto con un righello: una leggera inclinazione dello strumento può produrre un valore leggermente diverso ogni volta. Anche la temperatura in una stanza può oscillare a causa di una corrente d’aria improvvisa o di un cambio nell’umidità, generando letture instabili e variabili tra un rilevamento e l’altro.

Gli errori casuali nella misurazione, per certi versi, incarnano l'incertezza, l’imprevedibilità e la natura aleatoria della realtà stessa.

Sono il risultato di piccoli dettagli fuori dal nostro controllo (es. una vibrazione imprevista, una minuscola variazione di pressione, una frazione di secondo in più o in meno nella reazione umana) e sono sempre presenti.

Quindi, l'unico modo per affrontarli è gestirli tramite la statistica.

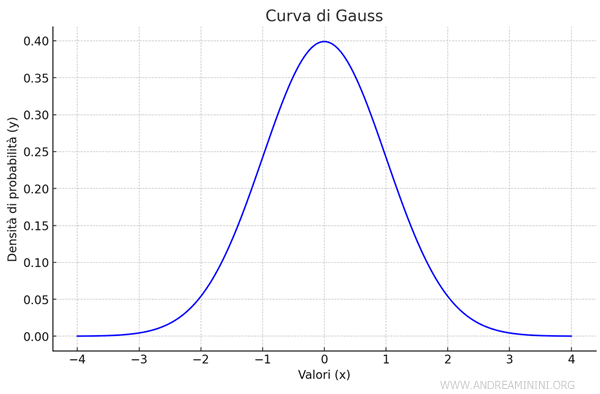
Ad esempio, è comune che questi errori si distribuiscano secondo una curva normale, dove la maggior parte dei risultati si avvicina al valore medio, mentre quelli estremi sono meno frequenti.

Quali sono le tecniche per gestire gli errori casuali?

Poiché gli errori accidentali non sono del tutto eliminabili, un metodo efficace per mitigarne l’effetto consiste nell’aumentare il numero di misurazioni e calcolarne la media.

Questa tecnica sfrutta la legge dei grandi numeri e la caratteristica della distribuzione normale.

In altre parole, ripetendo molte volte la misura, le fluttuazioni accidentali tendono a compensarsi, e il valore medio risulta più vicino a quello reale.

Un esempio pratico

Ho provato a misurare il tempo di caduta di una penna dal tavolo usando un cronometro, registrando cinque risultati.

Ogni volta, però, ho ottenuto un valore leggermente diverso, probabilmente a causa di piccoli errori di reazione nel fermare il cronometro al momento giusto.

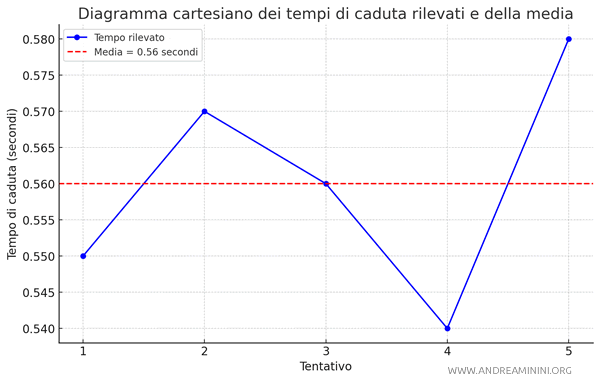
Ecco i tempi registrati, in secondi: 0,55; 0,57; 0,56; 0,54 e 0,58.

Tentativo	Tempo (secondi)
1	0,55
2	0,57
3	0,56
4	0,54
5	0,58

Queste differenze sono un esempio pratico di errore casuale.

Per ottenere un valore più affidabile del tempo di caduta, calcolo la media aritmetica dei risultati.

La media aritmetica si ottiene sommando i tempi e dividendo per il numero totale di misurazioni, come segue:

$$\text{Media} = \frac{0,55 + 0,57 + 0,56 + 0,54 + 0,58}{5}  = \frac{2,80}{5} = 0,56 \, \text{secondi}$$

Il valore medio di 0,56 secondi rappresenta così una stima più attendibile del tempo di caduta reale della penna, perché attenua l'effetto degli errori casuali presenti nelle singole misurazioni.

Esempio 2

Supponiamo ora che il cronometro sia tarato male e misuri il tempo più lentamente del dovuto.

Questo errore sistematico porta a una sovrastima del tempo di caduta in ogni misurazione.

Ecco i tempi registrati, con il cronometro tarato in modo errato:

Tentativo	Tempo (secondi)
1	0,65
2	0,67
3	0,66
4	0,64
5	0,68

Ora calcolo la media aritmetica delle rilevazioni:

$$\text{Media} = \frac{0,65 + 0,67 + 0,66 + 0,64 + 0,68}{5} = \frac{3,30}{5} = 0,66 \, \text{secondi}$$

In questo caso, ottengo una media di 0,66 secondi, un valore sistematicamente più alto rispetto al vero tempo di caduta.

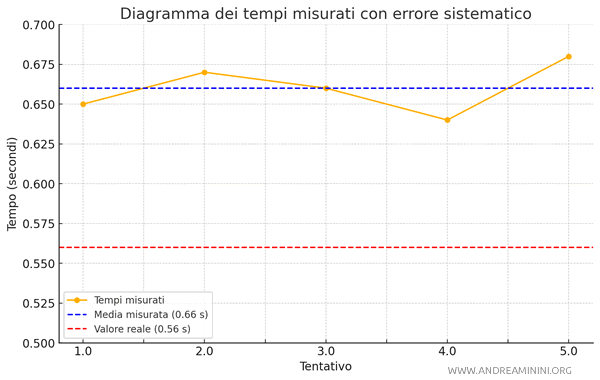
L’errore di taratura del cronometro ha infatti falsato tutte le misurazioni nello stesso senso, producendo valori maggiori del reale.

Nota. Questo esempio dimostra che un errore sistematico non può essere corretto semplicemente calcolando la media dei valori, ma richiede la taratura corretta dello strumento per ottenere misurazioni accurate.

E così via.