Lo scarto quadratico medio

Lo scarto quadratico medio (o deviazione standard) è la radice quadrata della media aritmetica dei quadrati degli scarti dei numeri dalla loro media aritmetica. $$ \sigma = \sqrt{ \frac{1}{n} \cdot \sum_{i=1}^n (x_i- \mu)^2 } $$ Dove μ è la media, x_i sono gli elementi della distribuzione e n è il numero di elementi della distribuzione. In genere si indica con la lettera greca sigma.

In altre parole, la deviazione standard è la radice quadrata della varianza.

Nel caso delle distribuzioni di frequenza la formula per calcolare lo scarto quadratico medio è

$$ \sigma = \sqrt{ \frac{1}{ \sum_{i=1}^k n_i} \cdot \sum_{i=1}^k (x_i- \mu)^2 \cdot n_i } $$

Dove n_i sono le frequenze mentre gli scarti (x_i-μ)² di ogni valore rispetto alla media sono detti scarti quadratici.

A cosa serve?

La deviazione standard (Std) è una misura di quanto i dati si distribuiscono intorno alla media.

E' molto più sensibile alle piccole variazioni dei dati intorno alla media rispetto allo scarto semplice medio.

Nota. Generalmente circa 2/3 degli elementi di una distribuzione sono compresi nell'intervallo (m-σ,m+σ). Quasi tutti gli elementi della distribuzione sono compresi nell'intervallo(μ-3σ,μ+3σ).

Un esempio pratico

Esempio 1

Questa distribuzione è composta da n=6 elementi.

$$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$

Calcolo la media aritmetica della distribuzione. E' uguale a μ=5

$$ \mu = \frac{1+5+7+3+6+8}{6 } = \frac{30}{6 } = 5 $$

Ora calcolo la varianza della distribuzione sapendo che n=6 e μ=5

$$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$

$$ \sigma^2 = \frac{1}{6} \cdot \sum_{i=1}^n (x_i - 5 )^2 $$

Sviluppo la serie di valori x₁=1, x₂=5, x₃=7, x₄=3, x₅=6, x₆=8

$$ \sigma^2 = \frac{1}{6} \cdot [ (1- 5 )^2+(5- 5 )^2+(7- 5 )^2+(3- 5 )^2+(6- 5 )^2+(8- 5 )^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ (-4 )^2+(0 )^2+(2)^2+(-2)^2+(1)^2+(3)^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ 16+0+4+4+1+9] $$

$$ \sigma^2 = \frac{34}{6} $$

La varianza della distribuzione è σ^₂=5,66

$$ \sigma^2 = 5,66 $$

Quindi, la deviazione standard (scarto quadratico medio) è la radice quadrata di 5,66

$$ \sigma = \sqrt{5,66} = 2,34 $$

Lo scarto quadratico medio è 2,34.

Esempio 2

Questa è distribuzione di frequenze

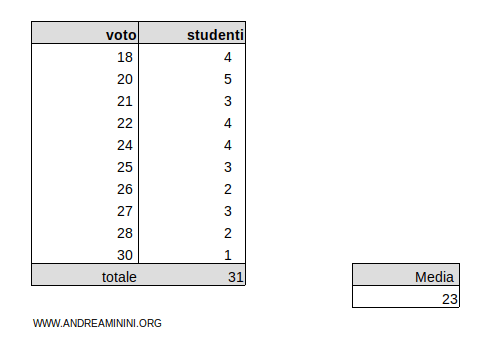
Calcolo la media aritmetica ponderata della distribuzione.

La media aritmetica è pari a μ=23

Calcolo la varianza della distribuzione.

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - \mu )^2 \cdot n_i $$

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - 23 )^2 \cdot n_i $$

La distribuzione è suddivisa in k=10 classi.

$$ \sigma^2 = \frac{1}{\sum_i^{10} n_i} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

La somma delle frequenze Σn_i=31

$$ \sigma^2 = \frac{1}{31} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

Calcolo i quadrati degli scarti degli elementi x₁=18, x₂=20, x₃=21, x₄=22, x₅=24, x₆=25, x₇=26, x₈=27, x₉=28, x₁₀=30 rispetto alla media ponderata μ=23

$$ \sigma^2 = \frac{(18 - 23 )^2 \cdot 4 + (20 - 23 )^2 \cdot 5 + (21 - 23 )^2 \cdot 3 + (22 - 23 )^2 \cdot 4 + (24 - 23 )^2 \cdot 4 + \\ + (25 - 23 )^2 \cdot 3 + (26 - 23 )^2 \cdot 2 + (27 - 23 )^2 \cdot 3 + (28 - 23 )^2 \cdot 2 + (30- 23 )^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{(-5)^2 \cdot 4 + (-3)^2 \cdot 5 + (-2)^2 \cdot 3 + (-1)^2 \cdot 4 + (1)^2 \cdot 4 + \\ + (2)^2 \cdot 3 + (3)^2 \cdot 2 + (4)^2 \cdot 3 + (5)^2 \cdot 2 + (7)^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{25 \cdot 4 +9 \cdot 5 + 4 \cdot 3 +1 \cdot 4 + 1 \cdot 4 +4 \cdot 3 + 9 \cdot 2 + 16 \cdot 3 + 25 \cdot 2 + 49 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{100 +45 + 12 +4 + 4 +12 + 18 + 48 + 50+ 49 }{31} $$

$$ \sigma^2 = \frac{342}{31} $$

La varianza della distribuzione di frequenze è σ^₂=11,03

$$ \sigma^2 = 11,03 $$

Quindi, la deviazione standard della distribuzione è la radice quadrata di 11,03

$$ \sigma = \sqrt{11,03} =3,32 $$

Qual è l'utilità dello scarto quadratico medio?

Lo scarto quadratico medio serve a quantificare quanto i valori di un insieme di dati si distribuiscono attorno alla media.

Il confronto tra la deviazione standard di due o più insiemi di dati mi aiuta a capire quale sia più variabile.

Esempio. Supponiamo di avere due classi di studenti che hanno preso voti su una scala da 1 a 10. In una classe A, i voti sono 4, 5, 6, 6, 7 e 8, mentre nell’altra classe B i voti sono 3, 3, 3, 9, 9, 9. In entrambi i casi, la media dei voti è 6. $$ \mu_A = \frac{4+5+6+6+7+8}{6} = \frac{36}{6} = 6 $$$$ \mu_B = \frac{3+3+3+9+9+9}{6} = \frac{36}{6} = 6 $$ Tuttavia, nella seconda classe c’è una maggiore variabilità nelle performance degli studenti, perchè la deviazione standard più alta. Questa informazione può aiutare gli insegnanti a identificare la classe che richiede più attenzione per livellare le competenze. In questo caso, la deviazione standard è \( \sigma_A = 1.29 \) per la classe A e \( \sigma_B = 3.0 \) per la classe B.    $$   \sigma_A= 1.29 $$ $$    \sigma_B =  3.0 $$Quindi, a parità di media dei voti, la classe B ha maggiore bisogno di un'attività extra di potenziamento e recupero degli studenti con i voti più bassi.

Pertanto, la deviazione standard non solo mi dice quanto i dati sono "sparpagliati", ma mi dà anche una misura per confrontare insiemi di dati in modo più oggettivo rispetto al solo uso della media.

A volte, questa informazione è anche legata al rischio e alle probabilità che un evento si verifichi o meno. 

Esempio. Se confronto due fondi d’investimento, entrambi con una media di ritorno del 5%, la deviazione standard può aiutarmi a valutare il rischio. Un fondo con una bassa deviazione standard ha un rendimento più stabile nel tempo, mentre uno con una deviazione standard elevata ha ritorni molto variabili, quindi è un investimento più rischioso. A parità di rendimento medio, un investitore razionale sceglie di minimizzare il rischio.

Inoltre, nel caso particolare delle distribuzioni normali, la deviazione standard mi dice anche quanto è probabile che un dato si trovi in un certo intervallo rispetto alla media.

Ad esempio, circa il 68% dei valori in una distribuzione normale cadono entro una deviazione standard (σ) dalla media, circa il 95% entro due deviazioni standard (2σ) e circa il 99% entro tre deviazioni standard (3σ).

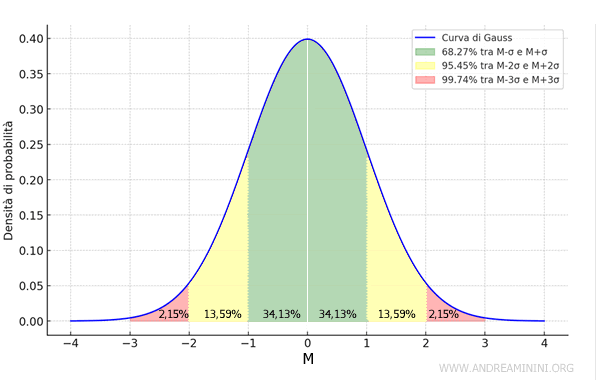
Questa informazione è fondamentale nelle attività di campionamento, quando voglio stimare le caratteristiche di un'intera popolazione partendo da un campione, cioè da una porzione limitata della popolazione.

E così via.