Le tabelle a doppia entrata
Le tabelle a doppia entrata sono strumenti utilizzati per rappresentare la relazione tra due caratteri statistici X e Y.
Sono utili per rappresentare una distribuzione congiunta o doppia (X,Y) in cui due caratteri statistici sono presenti simultaneamente in ogni unità statistica, poiché permettono di visualizzare le interazioni tra le due variabili statistiche.
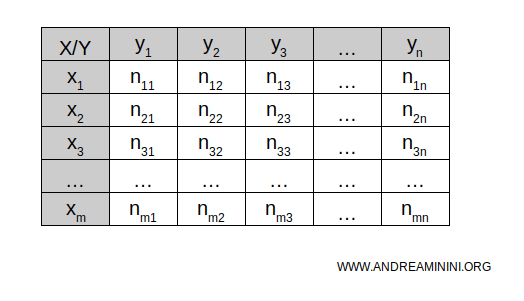
Queste tabelle vengono definite "a doppia entrata" perché incrociano le informazioni provenienti da due dimensioni o variabili, permettendo di esaminare la relazione tra di esse.
Sulle righe della tabella sono elencate le modalità del primo carattere statistico X, mentre sulle colonne sono rappresentate le modalità del secondo carattere statistico Y.

In ciascuna casella cella tabella indico la frequenza assoluta o relativa (njk) delle unità statistiche che presentano contemporaneamente le stesse modalità dei caratteri X e Y.
Queste frequenze interne alla tabella sono anche dette frequenze congiunte o interne.
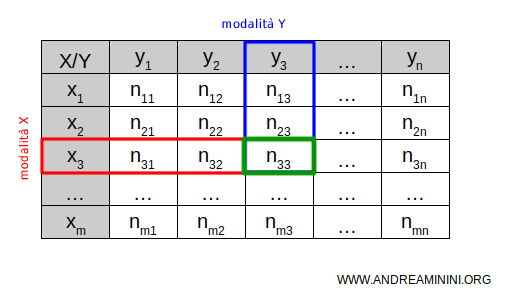
In questo modo, la tabella a doppia entrata mi permette di osservare due caratteri distinti delle stesse unità statistiche.
I totali della tabella a doppia entrata sono dette frequenze marginali e determinano le distribuzioni marginali, ossia le distribuzioni ottenute considerando un solo carattere, indipendentemente dall'altro.

Nota. Se entrambe le modalità sono quantitative, le tabelle a doppia entrata sono dette tabelle di correlazione o tabelle pivot. Viceversa, se sono qualitative sono dette tabelle di contingenza. Infine, se una modalità è quantitativa e l'altra qualitativa sono dette miste.
Un esempio pratico
Considero due serie statistiche in cui sono riportati i voti degli studenti di una classe.
La prima serie misura i voti in italiano mentre la seconda i voti in matematica di ciascun studente della classe.
| studenti | italiano | matematica |
|---|---|---|
| Alessandro | 7 | 6 |
| Alice | 8 | 7 |
| Andrea | 6 | 8 |
| Beatrice | 5 | 8 |
| Chiara | 8 | 8 |
| Davide | 9 | 7 |
| Elisa | 6 | 7 |
| Federica | 9 | 8 |
| Francesca | 9 | 7 |
| Gaia | 7 | 6 |
| Giovanni | 7 | 8 |
| Giulia | 9 | 6 |
| Irene | 8 | 5 |
| Luca | 7 | 6 |
| Marco | 5 | 6 |
| Martina | 7 | 5 |
| Matteo | 6 | 8 |
| Sara | 6 | 6 |
| Simone | 5 | 6 |
| Valentina | 6 | 6 |
Nota. In questo caso la popolazione è formata dai 20 studenti di una classe. Ogni studente è un'unità statistica. I caratteri sono due: i compiti in italiano e in matematica. I voti da 1 a 10 sono le modalità dei due caratteri.
Rappresento le modalità dei voti in italiano sulle colonne della tabella a doppia entrata e quelle dei voti in matematica sulle righe.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| Tot. | |||||||
In ciascuna casella della tabella indico le frequenze assolute, ossia quanti studenti hanno ottenuto una particolare combinazione di voti in italiano e in matematica.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 1 | 1 | 2 | ||||
| 6 | 3 | 2 | 3 | 1 | 9 | ||
| 7 | 1 | 1 | 2 | 4 | |||
| 8 | 2 | 1 | 1 | 1 | 5 | ||
| Tot. | 3 | 5 | 5 | 3 | 4 | 20 | |
Il risultato finale è una rappresentazione della correlazione tra i due fenomeni.
A colpo d'occhio mi permette di capire quanti studenti hanno un voto in italiano e un altro voto in matematica.
Nota. Da notare che la prima colonna, quella con i voti in matematica, e l'ultima colonna indicano la distribuzione marginale del voto in matematica di tutti gli studenti. Allo stesso modo la prima riga, quella con i voti in italiano, e l'ultima riga mostrano la distribuzione marginale del voto in italiano dell'intera popolazione.
Ogni singola colonna o riga rappresenta la distribuzione condizionata di una modalità rispetto a un valore dell'altra modalità.
Ad esempio, se considero la penultima colonna posso vedere la distribuzione condizionata del voto in matematica degli studenti che hanno preso 8 in italiano.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 1 | 1 | 2 | ||||
| 6 | 3 | 2 | 3 | 1 | 9 | ||
| 7 | 1 | 1 | 2 | 4 | |||
| 8 | 2 | 1 | 1 | 1 | 5 | ||
| Tot. | 3 | 5 | 5 | 3 | 4 | 20 | |
Le distribuzioni condizionate sono utili anche per calcolare le frequenze relative rispetto a una distribuziona marginale.
Questo è molto utile per verificare l'indipendenza o meno delle due variabili statistiche.
Ad esempio, calcolo le frequenze relative delle distribuzioni condizionate del voto in matematica tramite il rapporto di ogni frequenza assoluta per il totale della colonna.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 1/5 | 1/3 | 2/20 | ||||
| 6 | 3/3 | 2/5 | 3/5 | 1/4 | 9/20 | ||
| 7 | 1/5 | 1/3 | 2/4 | 4/20 | |||
| 8 | 2/5 | 1/5 | 1/3 | 1/4 | 5/20 | ||
| Tot. | 3/3 | 5/5 | 5/5 | 3/3 | 4/4 | 20/20 | |
In questo modo ottengo le frequenze relative.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 0.2 | 0.33 | 0.1 | ||||
| 6 | 1 | 0.4 | 0.6 | 0.25 | 0.45 | ||
| 7 | 0.2 | 0.33 | 0.5 | 0.2 | |||
| 8 | 0.4 | 0.2 | 0.33 | 0.25 | 0.25 | ||
| Tot. | 1 | 1 | 1 | 1 | 1 | 1 | |
Quando l'ultima colonna dei totali (distribuzione marginale) è uguale alle distribuzioni delle colonne precedenti (distribuzioni condizionate), le due modalità sono indipendenti.
In questo caso non hanno la stessa sequenza di frequenze relative, quindi tra le due modalità si ravvisa una certa dipendenza.
Un metodo alternativo per verificare l'indipendenza
In alternativa, per verificare l'indipendenza delle modalità posso anche calcolare le frequenze relative rispetto al totale (20) della popolazione.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 1/20 | 1/20 | 2/20 | ||||
| 6 | 3/20 | 2/20 | 3/20 | 1/20 | 9/20 | ||
| 7 | 1/20 | 1/20 | 2/20 | 4/20 | |||
| 8 | 2/20 | 1/20 | 1/20 | 1/20 | 5/20 | ||
| Tot. | 3/20 | 5/20 | 5/20 | 3/20 | 4/20 | 20/20 | |
Le due modalità sono indipendenti quando le frequenze relative congiunte sono il prodotto delle frequenze relative marginali.
| ITALIANO | |||||||
|---|---|---|---|---|---|---|---|
| MATEMATICA | 5 | 6 | 7 | 8 | 9 | Tot. | |
| 5 | 0.05 | 0.05 | 0.1 | ||||
| 6 | 0.15 | 0.1 | 0.15 | 0.05 | 0.45 | ||
| 7 | 0.05 | 0.05 | 0.1 | 0.2 | |||
| 8 | 0.1 | 0.05 | 0.05 | 0.05 | 0.25 | ||
| Tot. | 0.15 | 0.4 | 0.4 | 0.15 | 0.2 | 1 | |
In questo caso le frequenze relative congiunte non sono il prodotto delle frequenze relative marginali, quindi le due modalità sono dipendenti.
Ad esempio, se prendo la frequenza relativa congiunta 0.1 degli studenti che hanno preso 6 sia in matematica che in italiano, il prodotto delle rispettive frequenze relative marginali è 0.4 x 0.45 = 0.18 ed è diverso da 0.1.
Esempio 2
In questa tabella sono rappresentati i risultati di un'indagine condotta su 100 persone per verificare la correlazione tra il livello di istruzione (basso, medio, alto) e la preferenza per il tipo di film (commedia, azione, drammatico).
La tabella potrebbe apparire così:
| Livello di Istruzione | Commedia | Azione | Drammatico |
|---|---|---|---|
| Basso | 10 | 15 | 5 |
| Medio | 20 | 10 | 10 |
| Alto | 5 | 15 | 10 |
Questa tabella mostra, per esempio, che tra le persone con un livello di istruzione medio, 20 preferiscono i film commedia.
In questo caso entrambe le modalità (livello di istruzione e genere di film) sono qualitative, quindi si parla di tabella di contingenza.
E così via.
