I quartili

Cosa sono i quartili

I quartili sono tre indici di posizione (quantili) che dividono una distribuzione statistica in quattro parti uguali.

Ogni parte è un gruppo che ha lo stesso numero di elementi.

Esistono tre quartili

• Il primo quartile (Q₁) raggruppa a sinistra 1/4 degli elementi (25%) della distribuzione.
• Il secondo quartile (Q₂) raggruppa a sinistra 2/4 degli elementi (50%) della distribuzione
• Il terzo quartile (Q₃) raggruppa a sinistra 3/4 degli elementi (75%) della distribuzione

Esempio. In questa seriazione il primo quartile Q₁=4,5, il secondo quartile Q₂=6,5 e il terzo quartile Q₃=8,5 dividono la distribuzione in quattro parti. $$ X = \{ \underbrace{3,4}, \color{red}{Q_1}, \underbrace{5, 6}, \color{red}{ Q_2 } , \underbrace{7, 8}, \color{red}{Q_3} ,\underbrace{9, 10}, \} $$ A volte si parla anche di quartile zero (Q₀) per indicare il primo elemento della distribuzione ordinata (es. 3) a e di quarto quartile (Q₄) per indicare l'ultimo elemento della distribuzione ordinata (es. 11).

Come calcolare i quartili

Per calcolare i quartili uso due procedure a seconda se si tratta di una serie o di una distribuzione di frequenze.

Serie

Per calcolare i quartili di una serie di valori

1. Ordino la distribuzione dei valori in modo crescente
2. Moltiplico il numero degli elementi della serie per p=1/4 nel caso di Q₁ , per p=2/4 nel caso di Q₂ e per p=3/4 nel caso di Q₃ $$ k = n \cdot p $$
3. Calcolo la posizione del quartile
   • Se il prodotto k è un numero intero, ottengo la posizione del quartile facendo la media tra il k-esimo e il (k+1)-esimo elemento della distribuzione.
   • Se il prodotto k non è intero, ottengo la posizione del quartile arrotondando per eccesso k al primo intero successivo.

Distribuzioni di frequenze

Per calcolare i quartili in una distribuzione di frequenze

• Calcolo il cumulato delle frequenze assolute di ogni classe della distribuzione
• Divido il cumulato totale delle frequenze per 1/4, per 2/4 e per 3/4. In questo modo trovo la posizione del primo quartile (Q₁), del secondo quartile (Q₂) e del terzo quartile (Q₃) nelle frequenze cumulate.
• Trovo gli intervalli delle frequenze cumulate che comprendono le posizioni dei quartili Q₁, Q₂ e Q₃. Le rispettive classi di frequenza sono i quartili della distribuzione.

Nota. Non c'è un solo algoritmo per calcolare i quartili. Ne esistono diversi. Ad esempio, alcuni algoritmi utilizzano l'interpolazione lineare per trovare il valore del quartile in una classe. Altri metodi, invece, approssimano il quartile al valore centrale della classe.

Un esempio pratico

Esempio 1

Questa distribuzione è composta da n=9 elementi

$$ X = \{ 9,6,11,8,4,7,10,3,5 \} $$

Ordino la distribuzione dei valori X in modo crescente

$$ X = \{ 3,4,5,6,7,8,9,10,11 \} $$

Per calcolare il primo quartile (Q₁) moltiplico il numero degli elementi (n=9) per 1/4

$$ k = n \cdot \frac{1}{4} = 9 \cdot \frac{1}{4} =2,25 $$

Il prodotto è un numero decimale.

Quindi approssimo per eccesso la posizione del primo quartile alla prima posizione intera superiore (k=3).

$$ X = \{ 3,4,\color{red}{5}, 6,7,8,9,10,11 \} $$

Il terzo elemento (k=3) della serie è il valore 5.

$$ Q_1 = 5 $$

Pertanto, il primo quartile della distribuzione X è il valore Q₁=5

$$ X = \{ 3,4,\underbrace{5}_{Q_1}, 6,7,8,9,10,11 \} $$

Per calcolare il secondo quartile (Q₂) moltiplico il numero degli elementi (n=9) per 2/4

$$ k = n \cdot \frac{2}{4} = 9 \cdot \frac{2}{4} =4,5 $$

Il prodotto è un numero decimale.

Quindi, approssimo la posizione del secondo quartile alla prima posizione intera seguente (k=5) della serie.

$$ X = \{ 3,4, 5, 6,\color{red}{7},8,9,10,11 \} $$

Il quinto elemento (k=5) è il valore 7.

$$ Q_2 = 7 $$

Pertanto, il secondo quartile della serie è il valore Q₂=7

$$ X = \{ 3,4,5,6,\underbrace{7}_{Q_2} ,8,9,10,11 \} $$

Per calcolare il terzo quartile (Q₃) moltiplico il numero degli elementi (n=9) per 3/4

$$ k = n \cdot \frac{3}{4} = 9 \cdot \frac{2}{4} =6,75 $$

Il prodotto è un numero decimale.

Quindi, approssimo per eccesso la posizione del terzo quartile alla prima posizione intera successiva (k=7) della serie.

$$ X = \{ 3,4,5,6,7,8,\color{red}{9},10,11 \} $$

Il settimo elemento (k=7) è il valore 9.

$$ Q_3 = 9 $$

Pertanto, il terzo quartile della serie è il valore Q₃=9

$$ X = \{ 3,4,5,6,7,8,\underbrace{9}_{Q_3},10,11 \} $$

Complessivamente i tre quartili Q₁ = 5, Q₂ = 7 e Q₃ = 9 dividono la distribuzione in tre parti.

$$ X = \{ \underbrace{3,4}, \underset{ Q_1 }{ \color{red}5 }, \underbrace{6}, \underset{ Q_2 }{ \color{red}7 },\underbrace{ 9 }, \underset{ Q_3 }{ \color{red}5 }, \underbrace{10,11} \} $$

Nota. In questo caso i tre quartili sono valori approssimati che appartengono alla distribuzione X.

Esempio 2

Considero la precedente distribuzione eliminando un elemento.

Adesso la distribuzione è composta da n=8 elementi

$$ X = \{ 9,6,8,4,7,10,3,5 \} $$

Ordino la distribuzione X in modo crescente

$$ X = \{ 3,4,5,6,7,8,9,10 \} $$

Per calcolare il primo quartile (Q₁) moltiplico il numero degli elementi (n=8) per 1/4

$$ k = n \cdot \frac{1}{4} = 8 \cdot \frac{1}{4} =2 $$

Il prodotto k=2 è un numero intero.

Quindi, calcolo la media tra il valore alla posizione k=2 e quello alla posizione successiva k+1=3

$$ X = \{ 3,\color{red}4,\color{red}5,6,7,8,9,10 \} $$

Il secondo elemento (k=2) è il valore 4 mentre il terzo elemento (k=3) è il valore 5

Pertanto, il primo quartile della distribuzione X è il valore Q₁=4,5

$$ Q_1 = \frac{4+5}{2} = 4,5 $$

Per calcolare il secondo quartile (Q₂) moltiplico il numero degli elementi (n=8) per 2/4

$$ k = n \cdot \frac{2}{4} = 8 \cdot \frac{2}{4} =4 $$

Il prodotto k=4 è un numero intero.

Quindi, calcolo la media tra il valore alla posizione k=4 e quello alla posizione successiva k+1=5

$$ X = \{ 3,4,5,\color{red}6,\color{red}7,8,9,10 \} $$

Il quarto elemento (k=4) è il valore 6 mentre il quinto elemento (k=5) è il valore 7

Pertanto, il secondo quartile della distribuzione X è il valore Q₂=6,5

$$ Q_2 = \frac{6+7}{2} = 6,5 $$

Per calcolare il terzo quartile (Q₃) moltiplico il numero degli elementi (n=8) per 3/4

$$ k = n \cdot \frac{3}{4} = 8 \cdot \frac{3}{4} =6 $$

Il prodotto k=6 è un numero intero.

Quindi, calcolo la media tra il valore alla posizione k=6 e quello alla posizione successiva k+1=7

$$ X = \{ 3,4,5,6,7,\color{red}8,\color{red}9,10 \} $$

Il sesto elemento (k=6) è il valore 8 mentre il settimo elemento (k=7) è il valore 9

Pertanto, il terzo quartile della distribuzione X è il valore Q₃=8,5

$$ Q_3 = \frac{8+9}{2} = 8,5 $$

Complessivamente i tre quartili Q₁ = 4,5, Q₂ = 6,5 e Q₃ = 8,5 dividono la distribuzione in quattro parti.

$$ X = \{ \underbrace{3,4}, \color{red}{Q_1}, \underbrace{5, 6}, \color{red}{ Q_2 } , \underbrace{7, 8}, \color{red}{Q_3} ,\underbrace{9, 10}, \} $$

Nota. In questo caso i tre quartili sono valori approssimati che non appartengono alla distribuzione X.

Esempio 3

Considero questa distribuzione di frequenze.

Sono i voti di una sessione di esami a cui hanno partecipato 40 studenti.

Le modalità del fenomeno sono i voti da 18 a 30 mentre il numero degli studenti sono le rispettive frequenze assolute.

Per trovare i quartili aggiungo la colonna delle frequenze cumulate dalla prima modalità in poi.

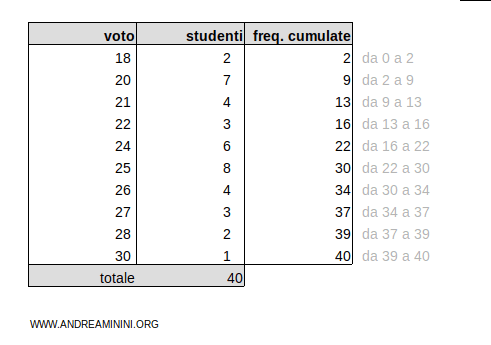
Il totale delle frequenze cumulate è f_tot=40

Per trovare il primo quartile moltiplico le frequenze cumulate f_tot=40 per 1/4

$$ k =f_{tot} \cdot \frac{1}{4} = 40 \cdot \frac{1}{4} = 10 $$

Il risultato 10 è compreso nell'intervallo 9-13 delle frequenze cumulate.

Pertanto, il primo quartile è la classe Q₁=21

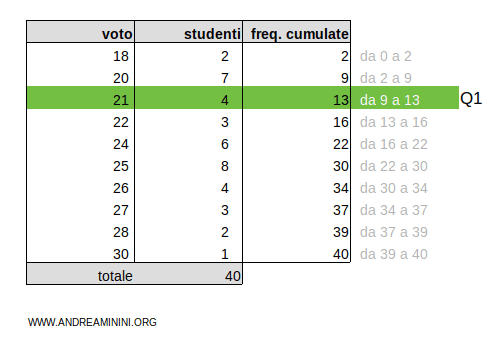
Per trovare il secondo quartile moltiplico le frequenze cumulate f_tot=40 per 2/4

$$ k =f_{tot} \cdot \frac{2}{4} = 40 \cdot \frac{2}{4} = 20 $$

Il risultato 20 è compreso nell'intervallo 16-22 delle frequenze cumulate.

Pertanto, il secondo quartile è la classe Q₂=24

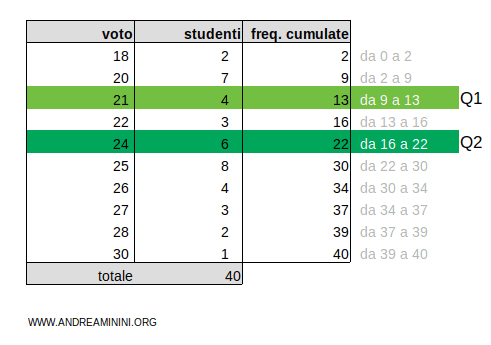
Per trovare il terzo quartile moltiplico le frequenze cumulate f_tot=40 per 3/4

$$ k =f_{tot} \cdot \frac{3}{4} = 40 \cdot \frac{3}{4} = 30 $$

Il risultato 30 è compreso nell'intervallo 30-34 delle frequenze cumulate.

Pertanto, il terzo quartile è la classe Q₃=26

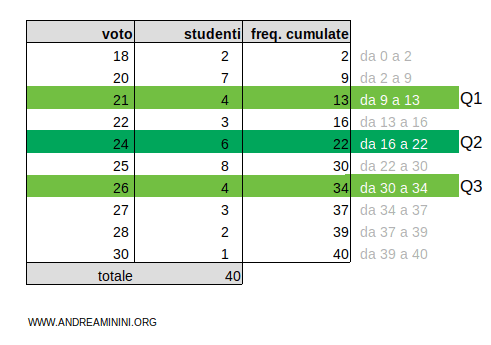
Nota. Mettendo i 40 voti in serie dal più piccolo al più grande, i tre quartili Q₁, Q₂, Q₃ sono le posizioni che dividono la serie in quattro parti uguali.

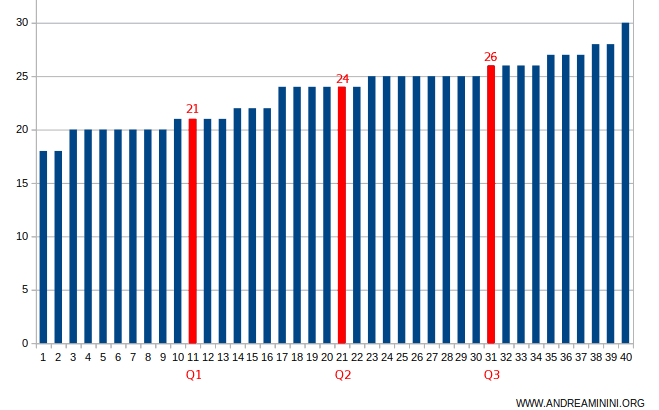
Esempio 4

Questa distribuzione di frequenza è suddivisa in classi

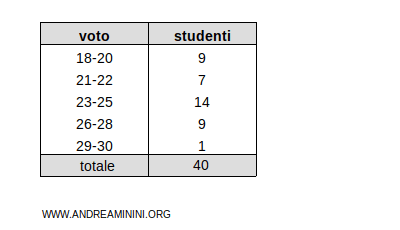
Aggiungo un'ulteriore colonna per ottenere le frequenze assolute cumulate

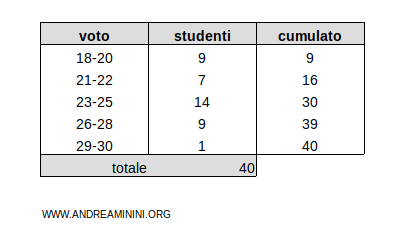
Il totale delle frequenze cumulate è f_tot=40

Per trovare il primo quartile Q₁ moltiplico le frequenze cumulate f_tot=40 per 1/4

$$ k =f_{tot} \cdot \frac{1}{4} = 40 \cdot \frac{1}{4} = 10 $$

Il risultato 10 è compreso nelle frequenze cumulate da 9 a 16 della classe 21-22.

In questo caso per ottenere il valore preciso del quartile uso l'interpolazione lineare.

$$ Q_1 = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

I termini hanno questo significato

• x_inf=21 e x_sup=22 sono gli estremi della classe 21-22
• c=10 è la posizione del primo quartile
• n_classe=7 è la frequenza della classe 21-22.
• n_prec=9 è la frequenza cumulata delle classi precedenti alla classe 21-22

A questo punto sostituisco i valori e svolgo i calcoli

$$ Q_1 = 21 + (22 - 21) \cdot \frac{ 10 - 9 }{7} $$

$$ Q_1 = 21 + 1 \cdot \frac{ 1 }{7} $$

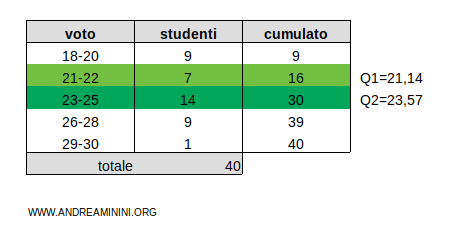
$$ Q_1 = 21,14 $$

Pertanto, il primo quartile è Q₁=21,14

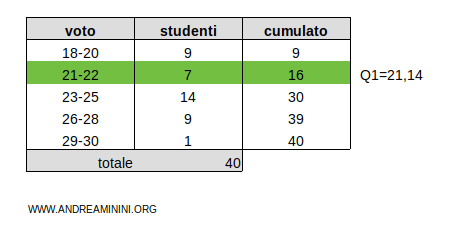
Nota. In alternativa per trovare il valore approssimato del primo quartile posso calcolare il valore centrale della classe. In questo caso, il valore centrale della classe 21-22 è 21,5. Pertanto, il valore approssimato del primo quartile è Q₁=21,5. Si tratta di un valore approssimato, meno preciso rispetto all'interpolazione lineare ma più rapido da calcolare.

Per calcolare il secondo quartile Q₂ moltiplico le frequenze cumulate f_tot=40 per 2/4

$$ k =f_{tot} \cdot \frac{2}{4} = 40 \cdot \frac{2}{4} = 20 $$

Il risultato 20 è compreso nelle frequenze cumulate da 16 a 30 della classe 23-25.

Utilizzo l'interpolazione lineare per conoscere il valore preciso del secondo quartile

$$ Q_2 = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

I termini hanno questo significato

• x_inf=23 e x_sup=25 sono gli estremi della classe 23-25
• c=20 è la posizione del secondo quartile
• n_classe=14 è la frequenza della classe 23-25.
• n_prec=16 è la frequenza cumulata delle classi precedenti alla classe 23-25

A questo punto sostituisco i valori e svolgo i calcoli

$$ Q_2 = 23 + (25 - 23) \cdot \frac{ 20 - 16 }{14} $$

$$ Q_2 = 23 + 2 \cdot \frac{ 4 }{14} $$

$$ Q_2 = 23,57 $$

Pertanto, il secondo quartile è Q₂=23,57

Nota. Usando il metodo del valore centrale, invece, il secondo quartile sarebbe pari a Q2=24. Dove 24 è il valore centrale della classe 23-25.

Per calcolare il terzo quartile Q₃ moltiplico le frequenze cumulate f_tot=40 per 3/4

$$ k =f_{tot} \cdot \frac{3}{4} = 40 \cdot \frac{3}{4} = 30 $$

Il risultato 30 è compreso nelle frequenze cumulate da 30 a 39 della classe 26-28.

Anche in questo caso uso l'interpolazione lineare per calcolare il valore preciso del terzo quartile

$$ Q_3 = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

I termini hanno questo significato

• x_inf=26 e x_sup=28 sono gli estremi della classe 26-28
• c=30 è la posizione del terzo quartile
• n_classe=9 è la frequenza della classe 26-28.
• n_prec=30 è la frequenza cumulata delle classi precedenti alla classe 26-28

A questo punto sostituisco i valori e svolgo i calcoli

$$ Q_3 = 26 + (28 - 26) \cdot \frac{ 30 - 30 }{9} $$

$$ Q_3 = 26 + 2 \cdot \frac{ 0 }{9} $$

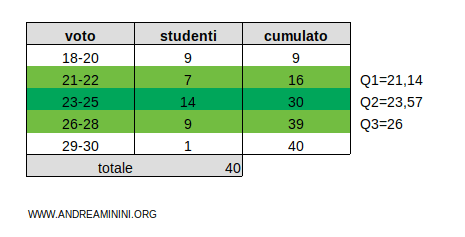
$$ Q_3 = 26 $$

Pertanto, il terzo quartile è Q₃=26

Il campo interquartile

Il campo interquartile è la differenza tra il terzo quartile (Q₃) e il primo quartile (Q₁) $$ Q_3 - Q_1 $$

Ad esempio, se i quartili di una distribuzione sono

$$ Q_1 = 4,5 $$

$$ Q_2 = 6,5 $$

$$ Q_3 = 8,5 $$

Il campo interquartile della distribuzione è 4

$$ Q_3 - Q_1 = 8,5 - 4,5 = 4 $$

E così via.