Percentili

Cosa sono i percentili

I percentili (o centili) sono 99 indici di posizione che dividono una distribuzione statistica in cento parti uguali.

Ogni parte è un gruppo con lo stesso numero di elementi.

Esistono novantanove percentili

• Il primo percentile (P₁) raggruppa a sinistra 1/100 degli elementi (1%) della distribuzione.
• Il secondo percentile (P₂) raggruppa a sinistra 2/100 degli elementi (2%) della distribuzione.
  :
• Il novantanovesimo percentile (P₉₉) raggruppa a sinistra 99/100 degli elementi (99%) della distribuzione

Esempio. In una serie di valori composta da 100 elementi, il cinquantesimo percentile P₅₀ è l'elemento che divide a metà i valori della distribuzione e coincide con la mediana. Il 25° percentile coincide con il primo quartile, il 20° percentile con il primo quintile, il 10° percentile con il primo decile. E via dicendo.

Come calcolare i percentili

Per calcolare i percentili uso due procedure a seconda se si tratta di una serie di valori o di una distribuzione di frequenze.

Serie

Per calcolare i percentili di una serie di valori

1. Ordino la serie di valori in modo crescente
2. Moltiplico il numero degli elementi della serie per p=1/100 nel caso di P₁ , per p=2/100 nel caso di P₂ , .... , per p=99/100 nel caso di P₉₉ $$ k = n \cdot p $$
3. Calcolo la posizione del percentile
   • Se il prodotto k è un numero intero, il percentile è la media dei valori nel k-esimo e il (k+1)-esimo elemento della serie.
   • Se il prodotto k non è intero, arrotondo per eccesso k al primo intero successivo. Il percentile è il valore che si trova nella posizione k della serie.

Distribuzioni di frequenze

Per calcolare i percentili in una distribuzione di frequenze

• Calcolo le frequenze assolute cumulate di ogni classe della distribuzione
• Divido il totale delle frequenze cumulate per 1/100, per 2/100, ... e per 99/100. In questo modo trovo la posizione del primo percentile (P₁), del secondo percentile (P₂) .... e del novantanovesimo percentile (P₉₉) nelle frequenze cumulate.
• Trovo gli intervalli delle frequenze cumulate che comprendono le posizioni dei percentili P₁, P₂ ... e P₉₉. Le rispettive classi di frequenza sono i percentili della distribuzione.

Nota. Ci sono diversi algoritmi per calcolare i percentili. Questo è soltanto una tra le tante procedure possibili. A volte si sceglie come percentile il valore centrale della classe. Altre volte si calcola il valore percentile per interpolazione lineare.

Un esempio pratico

Esempio 1

Questa distribuzione è composta da n=9 elementi

$$ X = \{ 9,6,11,8,4,7,10,3,5 \} $$

Ordino la distribuzione in modo crescente

$$ X = \{ 3,4,5,6,7,8,9,10,11 \} $$

Per calcolare il quarantacinquesimo percentile (P₄₅) moltiplico il numero degli elementi (n=9) per 45/100

$$ k = n \cdot \frac{45}{100} = 9 \cdot \frac{45}{100} =4,05 $$

Il prodotto è un numero decimale k=4,05.

Quindi approssimo per eccesso la posizione del 45° percentile alla prima posizione intera superiore (k=5).

$$ X = \{ 3,4,5, 6,\color{red}{7},8,9,10,11 \} $$

Il quinto elemento (k=5) della serie ordinata è il valore 7.

$$ P_{45} = 7 $$

Pertanto, il 45° percentile della distribuzione X è il valore P₄₅=7

$$ X = \{ 3,4,5, 6,\underbrace{7}_{P_{45}},8,9,10,11 \} $$

Per calcolare il settantaduesimo percentile (P₇₂) moltiplico il numero degli elementi (n=9) per 72/100

$$ k = n \cdot \frac{72}{100} = 9 \cdot \frac{72}{100} =6,48 $$

Il prodotto è un numero decimale k=6,48.

Quindi, approssimo la posizione del 72° percentile alla prima posizione intera seguente (k=7) della serie.

$$ X = \{ 3,4, 5, 6,7,8,\color{red}{9},10,11 \} $$

Il settimo elemento (k=7) è il valore 9.

$$ P_{72} = 9 $$

Pertanto, il 72° percentile della serie è il valore P₇₂=9

$$ X = \{ 3,4,5,6,7 ,8,\underbrace{9}_{P_{72}},10,11 \} $$

Nota. In questo caso il percentile è un valore che appartiene alla distribuzione X. Non è detto che sia sempre così.

Esempio 2

Considero la precedente distribuzione eliminando un elemento.

Adesso la distribuzione è composta da n=8 elementi

$$ X = \{ 9,6,8,4,7,10,3,5 \} $$

Ordino la distribuzione X in modo crescente

$$ X = \{ 3,4,5,6,7,8,9,10 \} $$

Per calcolare il cinquantesimo percentile (P₅₀) moltiplico il numero degli elementi (n=8) per 50/100

$$ k = n \cdot \frac{50}{100} = 8 \cdot \frac{50}{100} =4 $$

Il prodotto k=4 è un numero intero.

Quindi, calcolo la media tra il valore alla posizione k=4 e quello alla posizione successiva k+1=5

$$ X = \{ 3,4,5,\color{red}6,\color{red}7,8,9,10 \} $$

Il quarto elemento (k=4) è il valore 6 mentre il quinto elemento (k=5) è il valore 7

Pertanto, il 50° percentile della distribuzione X è il valore P₅₀=6,5

$$ P_{45} = \frac{6+7}{2} = 6,5 $$

Nota. In questo caso il valore del percentile non appartiene alla distribuzione X.

Esempio 3

Considero questa distribuzione di frequenze.

Sono i voti di una sessione di esami. Le modalità del fenomeno sono i voti da 18 a 30. Il numero degli studenti sono le rispettive frequenze assolute.

Per trovare i percentili aggiungo la colonna delle frequenze cumulate dalla prima modalità in poi.

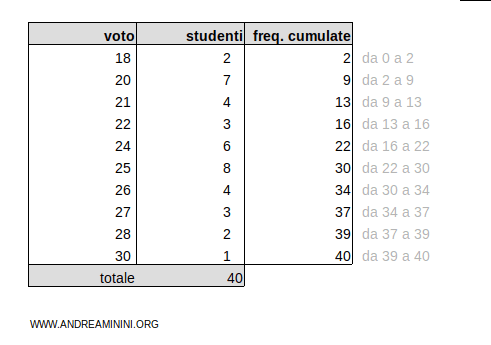
Il totale delle frequenze cumulate è f_tot=40

Per trovare il 45° percentile moltiplico le frequenze cumulate f_tot=40 per 45/100

$$ k =f_{tot} \cdot \frac{45}{100} = 40 \cdot \frac{45}{100} = 18 $$

Il risultato 18 è compreso nell'intervallo 16-22 delle frequenze cumulate.

Pertanto, il 45° percentile (P₄₅) è la classe 24

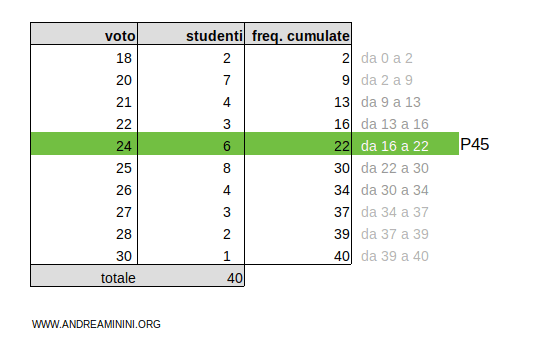
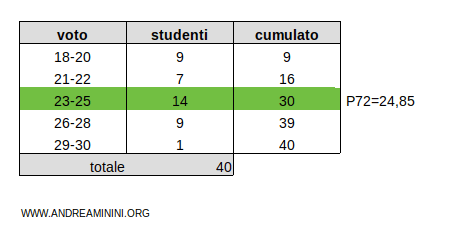
Esempio 4

Questa distribuzione di frequenza è suddivisa in classi

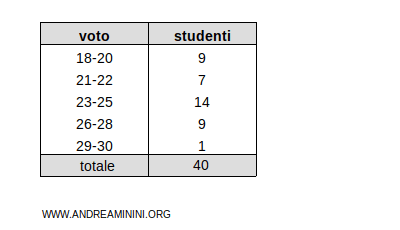
Aggiungo un'ulteriore colonna per ottenere le frequenze assolute cumulate

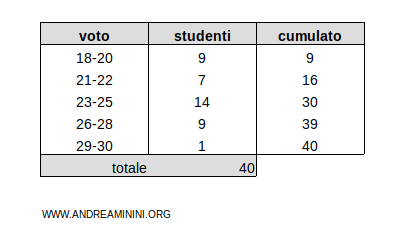
Il totale delle frequenze cumulate è f_tot=40

Per trovare il 72° percentile ( P₇₂ ) moltiplico le frequenze cumulate f_tot=40 per 72/100

$$ k =f_{tot} \cdot \frac{72}{100} = 40 \cdot \frac{72}{100} = 28,8 $$

Il prodotto è un numero decimale k=28,8. Quindi, lo arrotondo per eccesso al primo intero successivo k=29.

Il risultato k=29 è compreso nelle frequenze cumulate da 16 a 30 della classe 23-25.

In questo caso per ottenere il valore preciso del percentile uso l'interpolazione lineare.

$$ P_{45} = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

I termini hanno questo significato

• x_inf=23 e x_sup=25 sono gli estremi della classe 23-25
• c=29 è la posizione del percentile
• n_classe=14 è la frequenza della classe 23-25.
• n_prec=16 è la frequenza cumulata delle classi precedenti alla classe 23-25

A questo punto sostituisco i valori e svolgo i calcoli

$$ P_{72} = 23 + (25 - 23) \cdot \frac{ 29 - 16 }{14} $$

$$ P_{72} = 23 + 2 \cdot \frac{ 13 }{14} $$

$$ P_{72} = 24,85 $$

Pertanto, il 72° percentile è P₇₂=24,85

E così via.