La media aritmetica ponderata
La media aritmetica ponderata è una variante della media aritmetica in cui ciascun elemento è moltiplicato per un peso intero o decimale (w). La somma dei valori ponderati è divisa per la somma dei pesi. $$ \mu = \frac{\sum_{i=1}^k x_i \cdot w_i }{ \sum_{i=1}^k w_i } $$
Ad esempio, posso usare come peso la frequenza delle modalità in una tabella.
Posso anche decidere i pesi in modo arbitrario per dare maggiore importanza ad alcune modalità piuttosto che ad altre.
A cosa serve? La media aritmetica ponderata è spesso usata in economia e in finanza per tenere conto di diverse variabili o fattori che possono influire sui risultati dell'analisi. Ad esempio, in una serie temporale che misura il prezzo di mercato di un'azione negli ultimi 7 giorni, potrei usare la media ponderata per dare maggiore importanza all'ultimo termine (ultimo prezzo) rispetto ai termini precedenti.
Un esempio pratico
Uno studente svolge tre compiti A, B, C per passare l'esame di analisi matematica
Al primo compito (A) prende 18, al secondo compito (B) prende 22 e al terzo compito (C) prende 26.
La media aritmetica semplice dei tre compiti è
$$ \mu = \frac{18+22+26}{3} = \frac{66}{3} = 22 $$
Il professore decide però che i compiti hanno pesi diversi.
$$ w_A = 4 \\ w_B = 3 \\ w_C=2 $$
Il compito A pesa più del compito B e il doppio rispetto al compito C.
Per calcolare la media devo usare la media aritmetica ponderata.
$$ \mu = \frac{18 \cdot w_A +22 \cdot w_B +26 \cdot w_c}{w_A + w_B + w_C} $$
$$ \mu = \frac{18 \cdot 4 +22 \cdot 3 +26 \cdot 2}{4 + 3 + 2} $$
$$ \mu = \frac{72 +66 +52}{9} $$
$$ \mu = \frac{190}{9} = 21,1 $$
In questo caso la media ponderata è più bassa ( μ=21,1 ) rispetto alla media aritmetica semplice ( μ=22 ) perché il peso del primo compito (A) è più pesante rispetto agli altri.
Esempio 2
Considero questa tabella di dati
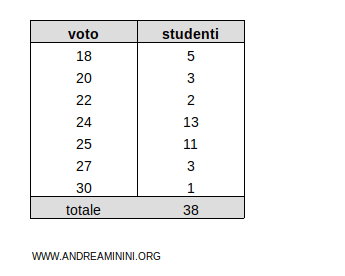
La prima colonna elenca le modalità del voto da 18 a 30 in un esame universitario.
La seconda colonna mostra le frequenze assolute di ciascun voto, ossia il numero di studenti che hanno preso un determinato voto.
Nota. Ad esempio, nella tabella cinque studenti hanno preso 18, tre studenti hanno preso 20, due studenti hanno preso 22, e via dicendo.
Calcolo la media aritmetica ponderata considerando le frequenze assolute come peso.
$$ \mu = \frac{\sum_{i=1}^k x_i \cdot w_i }{ \sum_{i=1}^k w_i } $$
Dove x sono i termini (voti) e n sono i pesi o frequenze (numero di studenti).
La media aritmetica ponderata è il rapporto tra la somma dei prodotti xn per la somma dei pesi.
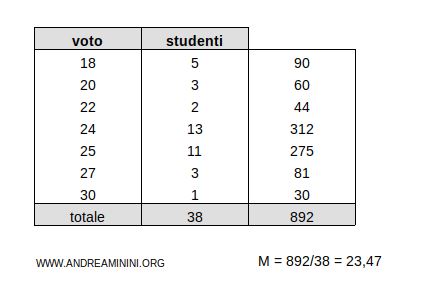
$$ \mu = \frac{18 \cdot 5 + 20 \cdot 3 + 22 \cdot 2 + 24 \cdot 13 + 25 \cdot 11 + 27 \cdot 3 + 30 \cdot 1}{5+3+2+13+11+3+1} $$
$$ \mu = \frac{90 + 60 + 44 + 312 + 275 + 81 + 30}{38} $$
$$ \mu = \frac{892}{38} $$
$$ \mu = 23,47 $$
La media aritmetica ponderata della distribuzione è μ=23,47
E così via.
