Le grandezze continue

Il postulato di continuità delle grandezze è una formalizzazione dell'idea intuitiva che le grandezze matematiche possono essere suddivise in parti sempre più piccole senza fine.

E' un concetto fondamentale per la comprensione della struttura dei numeri reali e per lo sviluppo dell'analisi matematica.

Spesso è associato a Georg Cantor e al suo lavoro sulla teoria degli insiemi e sulla fondazione della matematica moderna.

Nota. In termini più tecnici, il postulato di continuità afferma che ogni quantità può essere rappresentata come un insieme di unità indivisibili e che queste unità possono essere messe in corrispondenza uno-a-uno con i numeri interi. Cantor utilizzò questo principio per stabilire una base per la teoria degli insiemi e per esplorare concetti come la cardinalità e la costruzione dei numeri reali.

Uno degli aspetti chiave di questo postulato è l'idea di infinità divisibile delle grandezze, che gioca un ruolo fondamentale nel calcolo infinitesimale.

Ad esempio, quando considero la lunghezza di un segmento AB, il postulato di continuità implica che questo segmento può essere diviso in parti sempre più piccole, senza mai raggiungere una "parte più piccola indivisibile".

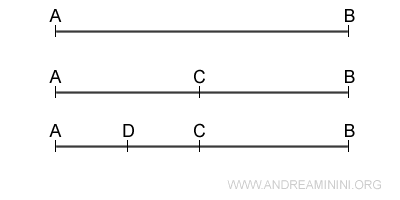
La capacità di dividere un segmento (o qualsiasi grandezza) in parti sempre più piccole senza raggiungere un limite indivisibile permette di trattare con precisione concetti come limiti, derivate e integrali.

Pertanto, il postulato di continuità di Cantor è stato fondamentale per lo sviluppo dell'analisi moderna e ha influenzato profondamente la direzione e la natura della matematica nel XX secolo.

Ha portato alla comprensione che i numeri reali possono essere visti come un continuum, ovvero insiemi infinitamente divisibili.

Esempio. Dati due numeri reali distinti qualsiasi a<b è sempre possibile un numero reale intermedio a<c<b.  Se prendo 2 e 3, tra questi ci sono infiniti numeri reali intermedi (es. 2.5, 2.49, 2.77, ...).  A sua volta anche  tra 2 e 2.5 ci sono infiniti numeri reali intermedi. E via dicendo.

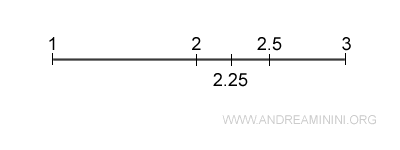
Si tratta di un concetto fondamentale per comprendere la densità dei numeri reali e, in generale, di un insieme numerico.

Questo ha contribuito a risolvere paradossi e problemi legati all'infinito e alla continuità nelle funzioni.

Ad esempio, il paradosso di Zenone illustra la difficoltà dei matematici dell'antica Grecia nel concepire l'infinito e la divisione infinita.

Zenone sosteneva che una lepre (o Achille) non potrebbe mai superare una tartaruga se la tartaruga avesse un vantaggio iniziale, poiché la lepre dovrebbe prima raggiungere il punto da cui la tartaruga era partita, e in quel tempo, la tartaruga si sarebbe spostata più avanti.

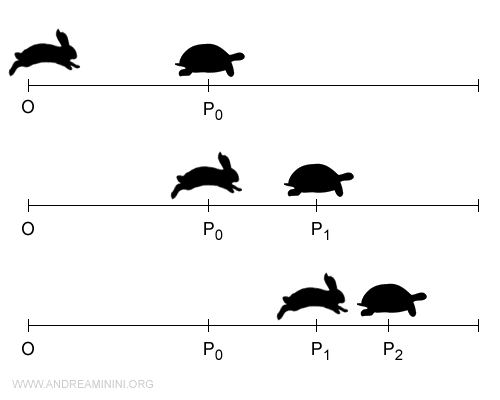
Il postulato della continuità ha avuto implicazioni dirette anche nello sviluppo del calcolo infinitesimale.

Le nozioni stesse di limite e continuità dipendono dall'idea che è possibile avvicinarsi arbitrariamente a un valore senza necessariamente raggiungerlo.

Questo è particolarmente importante nel calcolo di derivate e integrali, dove si lavora con quantità infinitesimamente piccole.

E così via.