Grandezze commensurabili e incommensurabili

Le grandezze commensurabili sono quelle grandezze omogenee che possono essere confrontate direttamente o misurate l'una in termini dell'altra, grazie alla presenza di un sottomultiplo comune.

In altre parole, due grandezze sono commensurabili se possono essere espresse come multipli di una stessa unità di misura.

Viceversa, se non è possibile, sono grandezze incommensurabili.

Ad esempio, la lunghezza e la larghezza di una stanza. Se misuro entrambe le lunghezze in metri, posso confrontarle direttamente perché entrambe sono espresse nella stessa unità di misura. In questo caso, lunghezza e larghezza sono commensurabili.

Se due grandezze omogenee A e B sono commensurabili, posso esprimerle con la stessa unità di misura (U)

$$ A = m \cdot U $$

$$ B = n \cdot U $$

Questo vuol dire che possono anche essere messe in relazione, ovvero che esiste un numero razionale m/n tale che le mette in relazione

$$ A = \frac{m}{n} \cdot B $$

E un altro numero n/m tale che le mette in relazione

$$ B = \frac{n}{m} \cdot A $$

Dove m e n sono due numeri interi.

Quindi, i rapporti m/n e n/m sono numeri razionali.

Dimostrazione. Considero la grandezza A $$ A = m \cdot U $$ Sapendo che l'unità di misura si può esprimere in relazione a entrambe le grandezze A e B $$ U = \frac{1}{m} \cdot A = \frac{1}{n} \cdot B $$ Quindi, se sostituisco U=(1/n)·B posso mettere in relazione le grandezze A e B tramite il rapporto m/n. $$ A = m \cdot U = m \cdot ( \frac{1}{n} \cdot B ) = \frac{m}{n} \cdot B $$ In alternativa, possono essere messe in relazione con il rapporto n/m $$ B = n \cdot U = n \cdot ( \frac{1}{m} \cdot A ) = \frac{n}{m} \cdot A $$

Pertanto, le grandezze commensurabili si riferiscono a grandezze che possono essere misurate l'una rispetto all'altra attraverso un rapporto espresso da un numero razionale.

Ad esempio

$$ A = \frac{m}{n} \cdot B $$

In altre parole, due grandezze sono commensurabili se il rapporto tra di esse è un numero m/n che può essere espresso come il quoziente di due interi.

Nota. Questo concetto ha origini antiche, risalenti al periodo dei Greci antichi, in particolare con i lavori dei pitagorici, che scoprirono che non tutti i rapporti tra lunghezze, aree o volumi sono esprimibili con numeri razionali, portando alla scoperta dei numeri irrazionali.

Un esempio pratico

Considero due segmenti AB e CD che hanno rispettivamente una lunghezza pari a 2 e 5 centimetri.

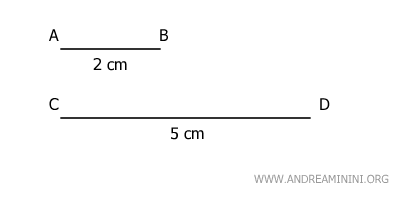
Sono due grandezze omogenee perché sono confrontabili e sono espresse con la stessa unità di misura.

Il segmento AB posso vederlo come multiplo di un centimetro secondo il numero due (n=2)

$$ \overline{AB} = 2 \cdot ( 1 \ cm ) $$

Anche il segmento CD posso ottenerlo come multiplo di un centimetro ma secondo il numero cinque (m=5).

$$ \overline{CD} = 5 \cdot ( 1 \ cm ) $$

Pertanto, le lunghezze di due segmenti AB e CD sono grandezze commensurabili perché hanno un sottomultiplo in comune.

In altre parole, sia AB che CD sono multipli di 1 cm.

$$ 1 \ cm = \frac{1}{2} \cdot \overline{AB} $$

$$ 1 \ cm = \frac{1}{5} \cdot \overline{CD} $$

Dove 1 cm è l'unità di misura (U) o, per dirla meglio, il numero 1 è la misura dell'unità di misura (cm).

$$ U = 1 \ cm = \frac{1}{2} \cdot \overline{AB} = \frac{1}{5} \cdot \overline{CD} $$

Questo vuol dire che posso esprimere una grandezza in termini dell'altra.

Se l'unità di misura è U=1 cm, il segmento AB diventa

$$ \overline{AB} = 2 \cdot U $$

Sapendo che U=(1/5)·CD

$$ \overline{AB} = 2 \cdot ( \frac{1}{5} \cdot \overline{CD} ) $$

$$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$

Quindi, il segmento AB ha una lunghezza pari a 2/5 del segmento CD.

Nota. Allo stesso modo posso dimostrare che il segmento CD ha una lunghezza pari a 5/2 del segmento AB $$ \overline{CD} = \frac{5}{2} \cdot \overline{AB} $$

Esempio 2

Se due grandezze omogenee sono espresse con la stessa unità di misura, non è detto che siano anche grandezze commensurabili.

Ad esempio, la lunghezza della diagonale e del lato di un quadrato sono due segmenti che hanno la stessa unità di misura (es. metri). Sono grandezze commensurabili o incommensurabili?

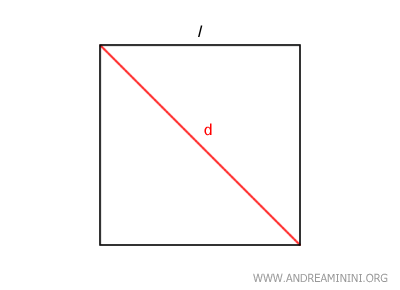
Pur avendo la stessa unità di misura, non esiste un numero razionale m/n che le metta in relazione.

Dalla geometria elementare so già che la lunghezza della diagonale (d) del quadrato è uguale alla lunghezza del lato (l) del quadrato moltiplicata per la radice quadrata di 2.

$$ d = l \cdot \sqrt{2} $$

Tuttavia, la radice quadrata di 2 è numero irrazionale, non è un numero razionale, ovvero non può essere espresso come rapporto di due numeri interi.

Pertanto, in questo caso posso affermare che la diagonale e il lato del quadrato sono grandezze incommensurabili usando i numeri razionali.

Osservazioni

Alcune mie osservazioni sulla commensurabilità delle grandezze

• Due grandezze omogenee incommensurabili possono essere confrontate con i numeri reali
  Il fatto che due grandezze omogenee siano incommensurabili non implica che non siano misurabili o confrontabili tra loro. In questo caso, però, non sono confrontabili tramite un numero razionale m/n, bensì tramite un numero reale (o irrazionale) α rispetto alla stessa unità di misura. $$ A = \alpha \cdot B \ \ \ \ \alpha \in $$

  Esempio. La diagonale (d) di un quadrato ha una lunghezza pari al prodotto tra la lunghezza del lato e il numero irrazionale √2 $$ d = l \cdot \sqrt{2}$$

• La commensurabilità nella fisica e matematica moderna
  Nella fisica e nella matematica moderna, la commensurabilità di due grandezze non è determinata dal fatto che il loro rapporto sia un numero razionale o irrazionale, ma piuttosto dalla loro capacità di essere misurate l'una in termini dell'altra utilizzando una misura comune. In questo contesto la commensurabilità si riferisce alla possibilità di descrivere diverse grandezze fisiche in termini di unità comuni o di relazioni matematiche, facilitando così la loro comparazione e comprensione all'interno di teorie unificate come la relatività o la meccanica quantistica.
• La commensurabilità nella fisica teorica
  In contesti più complessi della geometria elementare, come nella fisica teorica, il concetto di commensurabilità può essere più sfumato.

  Ad esempio, nella teoria della relatività di Einstein, concetti come tempo e spazio, tradizionalmente visti come separati, sono trattati come aspetti di una singola entità, lo spazio-tempo. Questo approccio unificato permette di considerare grandezze come tempo e spazio sotto una luce diversa, dove possono essere messe in relazione in modi che prima non erano considerati. Quindi, l'idea della commensurabilità può essere collegata al modo in cui Einstein ha trattato tempo e spazio, non come elementi separati e assoluti, ma come parti interconnesse di un tessuto più ampio, dove le misurazioni dell'uno possono influenzare e essere influenzate dall'altra.

E così via.