Grandezze inversamente proporzionali

Due grandezze omogenee A e B sono grandezze inversamente proporzionali se A aumenta quando B si riduce e viceversa, in modo tale da mantenere costante il prodotto di A per B. $$ k = A \cdot B $$

Un'altra maniera di vedere le cose è attraverso una formula: A = k/B, dove k è una costante. Se B aumenta, per mantenere la stessa k, A deve diminuire e viceversa.

$$ A = \frac{k}{B} $$

In altre parole, il rapporto tra due elementi qualsiasi a₁ e a₂ dell'insieme A è uguale al reciproco dei corrispondenti elementi b₁ e b₂ dell'insieme B.

$$ \frac{a_1}{a_2} = \frac{b_2}{b_1} $$

che equivale alla proporzione tra grandezze "a₁ sta a a₂ come b₂ sta a b₁"

$$ a_1 : a_2 = b_2 :  b_1 $$

Purché a2 e b1 siano diversi da zero, per evitare il problema di una divisione per zero.

Ad esempio, se A è inversamente proporzionale a B e il loro prodotto A·B=1 è sempre uguale a k=1, allora quando A è 2, B sarà 0.5, quando A è 4, B sarà 0.2. In tutti i casi, il prodotto è sempre uguale a 1.

Ad esempio, considero due elementi di A ,  4 e 2, il cui rapporto è uguale a 2 $$ \frac{4}{2} = 2 $$ Gli elementi corrispondenti dell'insieme B sono 0.25 e 0.50 e il loro rapporto è il reciproco di 2 ovvero 1/2 $$ \frac{0.25}{0.5} = \frac{ \frac{1}{4} }{ \frac{1}{2} } = \frac{1}{4} \cdot \frac{2}{1} = \frac{2}{4} = \frac{1}{2}  $$

In un grafico, le grandezze inversamente proporzionali sono rappresentate da una iperbole equilatera con l'asse trasverso sulla bisettrice, perché A aumenta quando B si riduce e viceversa ma il prodotto AB resta costante.

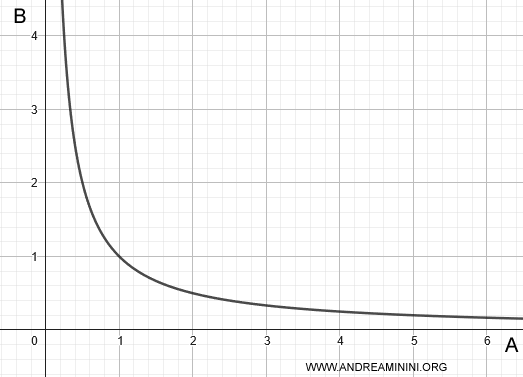
Nota. Questo concetto è molto utile in fisica, per esempio, nella legge di Coulomb dove la forza tra due cariche elettriche è inversamente proporzionale al quadrato della distanza tra le cariche.

Un esempio pratico

Considero la velocità e il tempo necessario per viaggiare una certa distanza.

$$ \text{tempo} = \text{distanza} / \text{velocità} $$

Se aumento la velocità, il tempo necessario per coprire quella distanza diminuisce, ma il prodotto della velocità per il tempo, che mi dà la distanza, rimane lo stesso.

$$  \text{velocità} \cdot \text{tempo} = \text{distanza} $$

Ad esempio, voglio percorrere una distanza di 100 km.

Se viaggio a una velocità di 50 km/h, il tempo necessario per percorrere questa distanza è di 2 ore.

$$ \text{Tempo} = \text{100 km} / \text{50 km/h} = \text{2 h} $$

Se raddoppio la velocità a 100 km/h, il tempo necessario per percorrere la stessa distanza è pari alla metà, ovvero a 1 ora.

$$ \text{Tempo} = \text{100 km} / \text{100 km/h} = \text{1 h} $$

In questo esempio, velocità (V) e tempo (T) sono inversamente proporzionali rispetto alla distanza percorsa, che rimane costante (100 km).

Quando la velocità raddoppia, il tempo si dimezza. Il prodotto di V e T in entrambi i casi è lo stesso: 100 km.

$$ \text{50 km/h} \cdot \text{2 ore} = \text{100 km} $$

$$ \text{100 km/h} \cdot \text{1 ora} = \text{100 km} $$

Questo dimostra come, mantenendo costante la distanza, aumentando la velocità si riduce proporzionalmente il tempo necessario per percorrerla.

E così via.