Le rette ortogonali nello spazio

Due rette qualsiasi sghembe nello spazio sono tra loro ortogonali ( perpendicolari ) se il prodotto scalare dei vettori direttori è zero. $$ < v_1 , v_2 > = 0 $$

Le rette possono essere anche sghembe, ovvero  rette che non giacciono sullo stesso piano e, di conseguenza, non si incontrano mai.

Dunque, per definizione, le rette sghembe sono non incidenti perché non hanno alcun punto in comune.

E' comunque possibile, anche in questo caso, calcolare l'angolo e verificare se sono rette ortogonali.

Un esempio pratico

Ho due rette nello spazio (x,y,z).

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} $$

I rispettivi vettori direttori sono

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} $$

Sono due rette sghembe non incidenti.

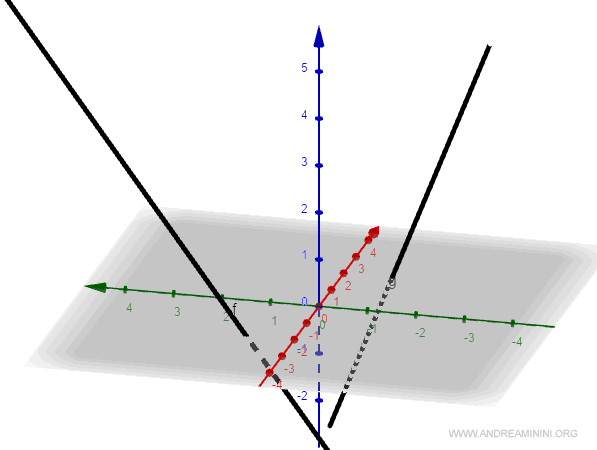
Le rette sono ortogonali?

Per rispondere calcolo il prodotto scalare dei loro vettori direttori.

$$ <v_1 , v_2 > = 2 \cdot1 + 1 \cdot 2 + 2 \cdot (-2) = 0 $$

Il prodotto scalare è nullo. Si tratta di due vettori ortogonali.

Pertanto, le due rette sono ortogonali.