Esercizio equazione differenziale 21
Devo studiare l'equazione differenziale del 1° ordine
$$ \begin{cases} y'=y-1 \\ \\ y(0)=7 \end{cases} $$
Si tratta di un problema di Cauchy in quanto è imposta come condizione iniziale y(0)=7
E' un'equazione differenziale lineare del tipo y'+a(x)y=b(x) con a(x)=-1 e b(x)=-1
$$ y'-y = -1 $$
Per risolverla applico il metodo della variazione delle costanti
$$ y= e^{-\int a(x) \ dx} \cdot [ \int b(x) \cdot e^{\int a(x) \ dx} \ dx + c] $$
Sostituisco a(x)=-1 e b(x)=-1
$$ y = e^{-\int -1 \ dx} \cdot [ \int-1 \cdot e^{\int -1 \ dx} \ dx + c] $$
$$ y = e^{\int 1 \ dx} \cdot [ - \int e^{- \int 1 \ dx} \ dx + c] $$
L'integrale ∫1 dx è la primitiva x
$$ y = e^x \cdot [ - \int e^{- x} \ dx + c] $$
L'integrale ∫e-x dx è la primitiva -e-x
$$ y = e^x \cdot [ - ( - e^x) + c] $$
$$ y = e^{x} \cdot [ e^{-x} + c] $$
$$ y = e^{x} \cdot (e^{-x}) + c \cdot e^{x} $$
$$ y = 1 + ce^{x} $$
Quindi la soluzione generale è
$$ y = ce^{x} + 1$$
Ora applico la condizione iniziale y(0)=7 con x=0
$$ 7 = ce^{0} + 1$$
$$ 7 - 1 = c \cdot 1 $$
$$ c = 6 $$
Pertanto, la soluzione del problema di Cauchy è la soluzione generale con c=8
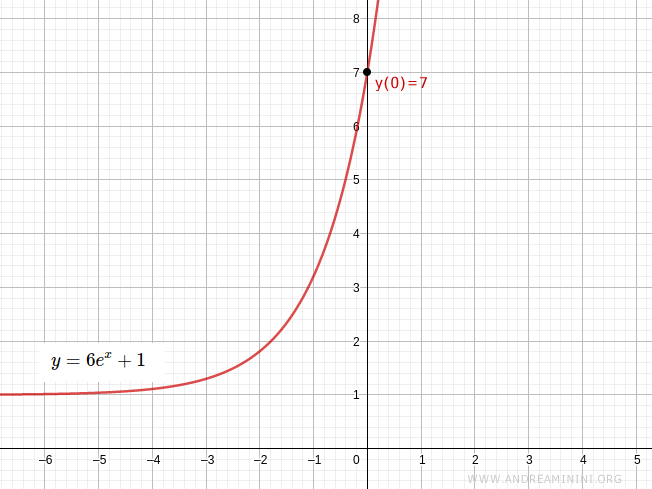
$$ y = 6e^{x} + 1$$
Verifica. Questa funzione passa nel punto y=7 quando x=0.
Inoltre, sostituendo la soluzione y=6ex+1 nell'equazione differenziale y'=y-1 ottengo $$ y'=y-1 $$ $$ D(6ex+1 )=( 6ex+1 ) -1 $$ $$ 6ex=6ex $$ L'identità è soddisfatta.
Soluzione alternativa
L'equazione differenziale posso risolverla anche con il metodo delle variabili separabili
$$ \begin{cases} y'=y-1 \\ \\ y(0)=7 \end{cases} $$
Separo le variabili
$$ y'=y-1 $$
$$ \frac{dy}{dx}=y-1 $$
$$ \frac{1}{y-1} dy= dx$$
Poi integro entrambi i membri per le rispettive variabili
$$ \int \frac{1}{y-1} \ dy= \int \ dx$$
Il primo integrale è il logaritmo log |y-1| +c1
$$ \log | y-1| + c_1= \int \ dx$$
Il secondo integrale è x+c2
$$ \log | y-1| + c_1= x+c_2 $$
Per semplificare considero un'unica costante c=c2-c1
$$ \log | y-1| = x+c $$
Quindi ricavo la funzione y
$$ e^{\log | y-1|} = e^{x+c} $$
Essendoci un modulo devo considerare due segni
$$ y-1 = \pm e^{x+c} $$
Quale dei due va scelto? Per capirlo devo considerare la condizione iniziale.
Sostituisco y(0)=7 e x=0
$$ 7-1 = \pm e^{0+c} $$
$$ 6 = \pm e^{c} $$
Essendo 6 un numero positivo scelgo il segno + anche al secondo membro
$$ y-1 = e^{x+c} $$
Nota. Un altro modo per ricavare il segno si ottiene semplificando gli esponenziali $$ y-1 = \pm e^{x+c} $$ $$ y-1 = \pm e^{x}e^c $$ sapendo che ec è una costante posso sostituirlo con la costante c $$ y-1 = \pm e^{x}c $$ La costante c può assumere sia numeri positivi che negativi, quindi posso eliminare il doppio segno $$ y-1 = e^{x}c $$ Il risultato finale è lo stesso.
Per semplificare ulteriormente applico le regole degli esponenziali
$$ y-1 = e^{x} e^c $$
Il termine ec è una costante quindi posso sostiturilo con il termine c
$$ y-1 = e^{x} \cdot c $$
Quindi la soluzione generale è
$$ y = ce^{x} +1 $$
E' la stessa soluzione ottenuta con il metodo precedente.
Quindi anche la soluzione del problema di Cauchy è la stessa.
E così via.
