La topologia discreta

La topologia discreta T è la topologia più grande possibile su un insieme X, poiché include tutti i possibili sottoinsiemi di X.

Nella topologia discreta, la collezione di insiemi aperti T include tutti i possibili sottoinsiemi di X.  Quindi, tutti i sottoinsiemi di X sono insiemi aperti.

Questo significa che ogni singolo elemento di X è considerato un "aperto" e quindi ogni punto è "isolato" dagli altri.

In altre parole, non ci sono restrizioni su come gli elementi possono essere vicini gli uni agli altri; ogni configurazione è permessa.  

La topologia discreta è chiamata "discreta" perché tratta gli elementi di X in modo separato e distinto, senza "sfumature" di vicinanza o continuità tra di loro.

È la topologia più grande che si può definire su un insieme, nel senso che non esiste una topologia che contenga più aperti di quella discreta, dato che include già tutti i possibili sottoinsiemi di X.

Nota. Questi criteri creano una struttura per gli insiemi aperti che ci permette di parlare di quanto gli elementi di uno spazio siano "vicini" o possano essere collegati senza interruzioni, ovvero la continuità.

Una particolarità importante da sottolineare in questa topologia è che:

Nella topologia discreta ogni sottoinsieme di uno spazio topologico è sia aperto che chiuso.

Questa proprietà deriva dal fatto che la topologia discreta definisce come "aperti" tutti i possibili sottoinsiemi di un dato spazio.

Di conseguenza, il complemento di ogni insieme dello spazio topologico è anch'esso un sottoinsieme aperto.

In topologia, un insieme è definito insieme chiuso se il suo complemento è aperto.

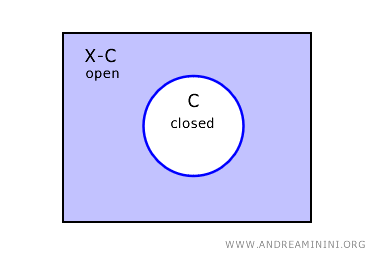
Pertanto, se il complemento di ogni sottoinsieme è aperto, allora ogni sottoinsieme è anche chiuso. 

Questa caratteristica della topologia discreta rende ogni sottoinsieme "clopen" ossia, contemporaneamente chiuso e aperto, indipendentemente da altre considerazioni.

Nota. Nella topologia discreta questa proprietà vale per ogni sottoinsieme, non solo per i singoli punti. Questo accade perché ogni singolo punto è un insieme aperto e ogni combinazione di punti è anch'esso un insieme aperto. Poiché il complemento di ogni possibile sottoinsieme è altresì un sottoinsieme dello spazio, e quindi aperto, ogni sottoinsieme è anche chiuso.

Un esempio pratico

Faccio un semplice esempio di topologia discreta utilizzando un insieme finito X composto da tre elementi.

$$ X = \{a, b, c\} $$

L'insieme delle parti dell'insieme X, ossia l'insieme di tutti i possibili sottoinsiemi di X, è composto dai seguenti sottoinsiemi:

• L'insieme vuoto: \(\emptyset\)
• I sottoinsiemi con i singoli elementi: \(\{a\}\), \(\{b\}\), \(\{c\}\)
• I sottoinsiemi con due elementi: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
• L'intero insieme: \(\{a, b, c\}\)

Nella topologia discreta su X, ogni possibile sottoinsieme di X è considerato un insieme aperto.

Quindi, la topologia discreta \(T\) su \(X\) è data da:

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\} $$

In questa topologia, ogni sottoinsieme di \(X\) è aperto per definizione.

Nota. Si tratta di una topologia perché include l'insieme X e l'insieme vuoto. Inoltre, qualsiasi intersezione e unione dei sottoinsiemi aperti è ancora parte della collezione T. Poiché in una topologia tutti i sottinsiemi sono aperti, ne deduco che non c'è nessuna restrizione sulla vicinanza e sulla continuità tra gli elementi dell'insieme X.

Ora se considero il sottoinsieme $ \{ a \} $ questo è un insieme aperto per la definizione stessa della topologia discreta.

Tuttavia, il sottoinsime $ \{ a \} $ è contemporaneamente anche un insieme chiuso perché il suo complemento $ X/ \{a\} = \{b,c\} $ è un insieme aperto. Un insieme chiuso è il complemento di un insieme aperto.

Quindi, nella topologia discreta il sottoinsieme $ \{ a \} $ è sia aperto che chiuso.

Lo stesso vale per ogni altro sottoinsieme della topologia.

E così via.