Topologia

La topologia è un ramo della matematica che studia le proprietà degli spazi che rimangono invariate dopo trasformazioni continue (come stirare, piegare, torcere). Ad esempio, la connessione, la compattazione e il numero di buchi in un oggetto, ecc.

In altre parole, la pologia si concentra su come gli spazi sono configurati o connessi, piuttosto che su misure esatte come distanza o grandezza.

Nel contesto della topologia, concetti come distanza e misura dell'ampiezza angolare sono irrilevanti, ciò che conta è la qualità delle forme e la possibilità di trasformarle.

La topologia introduce il concetto di spazio topologico e le trasformazioni chiave in topologia sono gli omeomorfismi.

La topologia è spesso descritta come una "geometria del caucciù" perché immagina gli oggetti come se fossero fatti di materiale elastico che può essere stirato o compresso ma non strappato o incollato. E' una parte essenziale della matematica moderna.

La storia

La topologia ha avuto il suo sviluppo iniziale nel XVIII secolo.

Ha origini che risalgono al problema dei Sette Ponti di Königsberg di Leonhard Euler, che introdusse concetti fondamentali di connessione e rete.

Questo problema ha portato alla formulazione di domande fondamentali relative alle proprietà degli spazi, gettando le basi per lo sviluppo della topologia come disciplina matematica.

Il problema dei sette ponti. In un'isola fluviale ci sono sette ponti. Scegliendo un punto iniziale qualsiasi, quale percorso consente di passare una e una sola volta in tutti i sette ponti? Sottolineo che, per risolvere il problema, non si può ripassare sullo stesso ponte più di una volta.

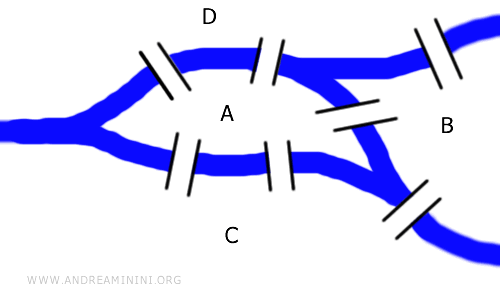
In questo problema non occorre conoscere le distanze, quanti metri sono lunghi i ponti o quanto distano tra loro. E' un tipico problema topologico che posso rappresentare anche tramite i grafi. Il grafo seguente è topologicamente equivalente alla mappa dei ponti iniziale.

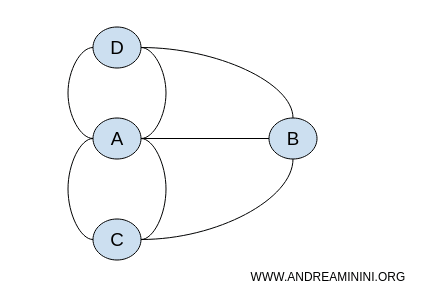
Inoltre, non importa come sia la disposizione dei nodi del grafo. Ciò che conta sono le connessioni tra i nodi. Quindi, potrei rappresentare il problema con infiniti grafi diversi tra loro ma topologicamente equivalenti.

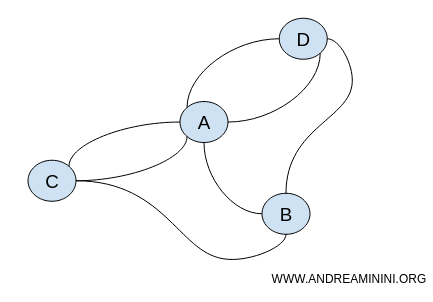
Entrambi i grafici mantengono le stesse proprietà topologiche ossia le stesse connessioni e continuità.

Euler si rese conto che il problema dei Sette Ponti di Königsber, pur essendo geometrico, non richiedeva la determinazione delle grandezze. 

Si rese conto che il problema dipendeva essenzialmente dalla posizione e dimostrò che non aveva soluzione. Nacque così la "geometria della posizione".

Nel corso del XIX secolo altri matematici come Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann, Felix Klein esplorarono le proprietà delle forme e delle superfici, gettando le basi per la comprensione delle proprietà topologiche.

Nota. Il primo a usare il termine "topologia" fu Listing nel 1847. Tuttavia, il termine venne accolto dalla comunità scientifica solo qualche decennio dopo.

Nel XIX secolo la geometria della posizione trovò numerose applicazioni pratiche. Ad esempio, nello studio delle reti elettriche di Gustav Kirchhoff.

Successivamente Henri Poincaré nel tardo XIX e inizio XX secolo contribuì alla geometria della posizione lavorando nella topologia algebrica.

Nel XX secolo la topologia si suddivise in discipline specialistiche, come la topologia algebrica e la topologia generale, ottenendo contributi significativi da parte di matematici come Felix Hausdorff, Cantor e Brouwer. In particolar modo nella matematica astratta.

La topologia divenne così un campo fondamentale della matematica che pone la sua attenzione sulla comprensione delle proprietà degli spazi che rimangono invariate sotto trasformazioni continue.

Oggi la topologia comprende diverse sotto-discipline, come la topologia algebrica, la topologia differenziale, la topologia generale e la topologia geometrica. Ognuna di queste aree si concentra su aspetti diversi degli spazi topologici.

In generale, la topologia può essere vista in una prospettiva più ampia come lo studio generale delle forme e in una prospettiva teorica come un disciplina della matematica astratta.

Nonostante la sua natura astratta, i concetti topologici si applicano a diversi problemi reali in vari campi del sapere come l'economia, l'ingegneria e in varie discipline scientifiche.

 Spazi topologici

Uno spazio topologico è un concetto matematico che consiste in un insieme X accompagnato da una struttura T denominata "topologia".

$$ (X,T) $$

Questa struttura fornisce un quadro per comprendere nozioni astratte quali la continuità, la prossimità tra elementi, e la nozione di limite, in un modo che è più ampio e generale rispetto a quello tradizionalmente usato nella geometria o nell'analisi matematica.

Esempio. Un esempio classico di spazio topologico è la linea numerica reale \( \mathbb{R} \) con la sua topologia usuale. In questa topologia, un insieme è considerato aperto se, per ogni punto nell'insieme, esiste un intervallo intorno a quel punto che è completamente contenuto nell'insieme. Questo permette di definire e analizzare concetti come la continuità e i limiti in termini topologici.

Gli omeomorfismi

Un omeomorfismo è una trasformazione biunivoca e continua tra due spazi topologici, con una funzione inversa che è anch'essa continua, preservando le proprietà topologiche fondamentali.

Due spazi sono considerati essenzialmente gli stessi in topologia se esiste un omeomorfismo tra di loro.

Esempio. Un esempio classico di omeomorfismo è la trasformazione di una tazza da caffè in una ciambella. Entrambi hanno un unico "buco" (il manico della tazza e il buco centrale della ciambella) e possono essere trasformati l'uno nell'altro mediante una serie di deformazioni continue senza tagli o incollature, preservando così le loro proprietà topologiche essenziali.

La differenza tra la geometria e la topologia

In generale la topologia e la geometria sono due discipline distinte e autonome, perché si focalizzino su aspetti diversi degli spazi matematici. Sebbene ci siano anche dei collegamenti.

• Geometria
  La geometria si occupa delle proprietà degli spazi che sono relative a distanze, angoli e misure. Le origini della geometria si trovano nello studio di figure concrete nello spazio, come punti, linee, cerchi e poligoni, e le loro relazioni in termini di distanza e angolazione. Ad esempio, la rotazione di una figura è una tipica trasformazione geometrica che non modifica le distanze tra i punti.
  

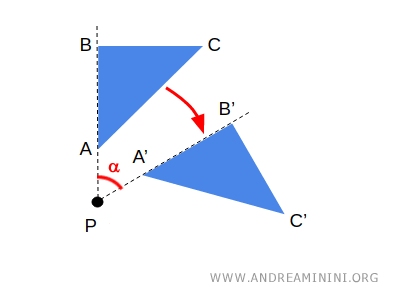
  La geometria euclidea è l'esempio più noto, ma ci sono anche geometrie non euclidee che esplorano concetti in assenza o in contrasto con il quinto postulato di Euclide (il postulato delle parallele).

• Topologia
  La topologia si concentra sulle proprietà degli spazi che rimangono invariate sotto trasformazioni continue. Queste trasformazioni possono includere stiramento e compressione, ma non taglio o incollaggio. La topologia si interessa di concetti come la continuità, la connessione, il numero di buchi, e la compattazione. Non è interessata alle misure esatte o alle forme precise, ma piuttosto alla natura qualitativa degli spazi. Ad esempio, la trasformazione di un cubo in una sfera è una trasformazione topologica, perché non modifica la connessione tra i punti, né la continuità. In altre parole, posso distorcere e compattare il cubo, senza strapparlo, fino a farlo diventare una sfera, 
  

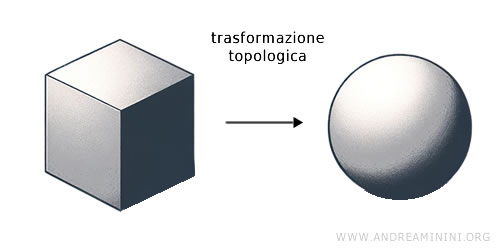
  Esempio. Provo a spiegarlo in modo più semplice, se ho un cubo fatto con la plastilina, posso comprimerlo con la mano dandogli una forma sferica, senza strappare o incollare dei pezzi. Alla fine non ho più un cubo ma una sfera. E viceversa, con altri movimenti posso comprimere la sfera di plastilina ai lati fino a farla tornare un cubo. E' un esempio di omeomorfismo, una delle principali trasformazioni topologiche.
  

Nonostante le loro differenze, topologia e geometria sono strettamente connesse.

La topologia può essere vista come una generalizzazione della geometria.

Mentre la geometria si occupa di proprietà rigide degli spazi, la topologia considera proprietà più flessibili e astratte.

In sintesi, la topologia è una branca autonoma della matematica che ha forti legami con la geometria, ma si concentra su aspetti differenti degli spazi matematici.

Le discipline della topologia

Le topologie si applicano in diversi rami della matematica e delle scienze.

• Topologia in geometria
  In geometria, la topologia si occupa dello studio delle proprietà delle figure che rimangono invariate attraverso trasformazioni continue come stiramenti, contrazioni e piegature, ma non strappi o incollature. Questo significa che la topologia geometrica si interessa di proprietà come la continuità, la connessione, la compattezza e i confini di spazi geometrici, senza considerare le distanze.
• Topologia generale (o topologia dei punti insieme)
  La topologia generale, anche nota come topologia dei punti insieme, studia le proprietà degli spazi topologici in modo molto astratto e generale. Si occupa di concetti come aperto, chiuso, continuità, compatezza, connessione, spazi metrici e spazi di funzioni. Ad esempio, la topologia degli insiemi aperti.
• Topologia algebrica
  La topologia algebrica studia gli spazi topologici attraverso strumenti provenienti dall'algebra, come i gruppi e gli anelli. Si focalizza sull'associazione di strutture algebriche agli spazi topologici per investigare le loro proprietà topologiche.  .
• Topologia differenziale
  La topologia differenziale si occupa delle proprietà e delle strutture degli spazi topologici che possono essere studiate usando il calcolo differenziale. In particolare, si concentra sugli spazi di varietà, che sono spazi che localmente somigliano allo spazio euclideo, consentendo la definizione di concetti come tangenza, differenziabilità e flusso. 
• Topologia applicata
  La topologia applicata si riferisce all'uso di metodi topologici in contesti pratici, spesso al di fuori della pura matematica. Questo può includere l'analisi dei dati ad alta dimensione, la scienza delle reti, l'ingegneria, la biologia computazionale, e altro ancora.

Ogni disciplina della topologia ha i suoi oggetti di studio, i suoi metodi e le sue applicazioni.

E così via.