Interno o parte interna di un insieme

L'interno di un insieme $ A $ in uno spazio topologico $ X $ è l'unione di tutti gli insiemi aperti contenuti in $ A $. Per indicarlo si usa il simbolo $ Int(A) $ o semplicemente $ A^\circ $.

L'interno, o parte interna di un insieme, è il più grande insieme aperto che è completamente contenuto all'interno di $ A $.

Non esiste un altro insieme aperto contenuto in $ A $ che sia più grande dell'interno di $ A $.

Nota. Questo è garantito dalla definizione stessa, poiché l'interno è l'unione di insiemi aperti. Quindi, è anch'esso un insieme aperto.

Formalmente, posso definire la parte interna dell'insieme A come l'insieme di tutti i punti di $ A $ per i quali esiste un intorno aperto completamente contenuto in $ A $.

$$ Int(A) = \bigcup \{ U \subseteq A : U \text{ è aperto in } X \} $$

In altre parole, per ogni punto $ x $ nell'interno di $ A $, esiste almeno un insieme aperto $ U $ tale che $ x \in U \subseteq A $.

In ogni caso, è essenziale tenere presente che l'interno di un insieme $ A $ dipende dalla struttura topologica $ X $ che contiene l'insieme A, non dipende dalle proprietà dell'insieme A. Pertanto, a seconda della struttura topologica $ X $ che ospita l'insieme $ A $, l'interno di $ A $ può cambiare.

Un esempio pratico
Il teorema dell'interno di un insieme
Le proprietà degli interni
Osservazioni

Un esempio pratico

Considero l'insieme $ A = [0, 1] $ in $ \mathbb{R} $ con la topologia standard.

Si tratta dell'intervallo chiuso che comprende tutti i numeri reali da 0 a 1 inclusi.

In questo caso l'interno di $ A $ è $ (0, 1) $.

$$ Int (A) = (0,1) $$

Questo è l'insieme aperto più grande di punti tra 0 e 1 che esclude i bordi 0 e 1, che non sono contenuti in alcun intervallo aperto completamente contenuto in $ A $.

Esempio 2

Ora studio l'insieme $ A = [0, 1) $ in $ \mathbb{R} $ con la topologia standard.

Questo insieme comprende tutti i numeri reali da 0 incluso fino a 1 escluso, formando così un intervallo chiuso a sinistra e aperto a destra.

La parte interna di $ A $ è sempre l'insieme aperto $ (0,1) $, come nell'esempio precedente:

\[ \text{Int}(A) = (0,1) \]

Questo accade perché per la definizione di interno in uno spazio topologico, esso consiste nell'unione di tutti gli insiemi aperti completamente contenuti nell'insieme originale.

Nota. In $ \mathbb{R} $ con la topologia standard, gli intervalli aperti sono la forma base degli insiemi aperti. Quindi, l'unico insieme aperto massimale contenuto in $ [0, 1) $ è $ (0,1) $, dato che non include il bordo chiuso a 0, che non è racchiuso da alcun intervallo aperto contenuto completamente in $ [0, 1) $. Pertanto, $ (0,1) $ rappresenta l'insieme di tutti i punti di $ A $ che possono essere circondati da intervalli aperti completamente contenuti in $ A $, soddisfacendo così la definizione di interno.

Esempio 3

In questo esempio, esamino l'insieme $ A = [0,1) $ quando $ X $ è dotato della topologia discreta.

In uno spazio topologico con topologia discreta, ogni singolo sottoinsieme di $ X $ è considerato un insieme aperto.

Questo significa che ogni elemento di $ A $ può essere circondato da un intorno che è completamente contenuto in $ A $ e consiste in qualsiasi combinazione di elementi di $ A $.

Nella topologia discreta su $ \mathbb{R} $, ogni singolo sottoinsieme di un insieme è considerato un insieme aperto. Questo include non solo tutti gli intervalli aperti o chiusi, ma anche qualsiasi combinazione arbitraria di punti, indipendentemente da come sono distribuiti. Quindi, sono insiemi aperti sia gli intervalli aperti come $ (0,0.5) $, $ (0.25,0.75) $, o $ (0,1) $ che gli intervalli chiusi come $ [0,0.25] $ compresi in $ A=[0,1) $, oltre all'insieme vuoto, e l'intero intervallo $ [0,1) $ stesso.

In particolare, dato che ogni sottoinsieme è aperto, anche $ A = [0,1) $ stesso è un insieme aperto in questa topologia.

Pertanto, l'interno di $ A $ in questo contesto è $ A $ stesso, perché ogni punto in $ A $ ha come intorno aperto un sottoinsieme che include il punto stesso e che è completamente contenuto in $ A $.

$$ \text{Int}(A) = A = [0,1) $$

Quindi, in una topologia discreta, l'interno di un insieme coincide sempre con l'insieme stesso.

Nota. Questo risultato dimostra come la scelta della topologia può influenzare la natura degli intorni e degli interni degli insiemi. Come precedentemente sottolineato, le proprietà di un intorno di un insieme dipendono dalla struttura topologica $ X $ all'interno della quale è definito l'insieme $ A $.

Esempio 4

Considero uno spazio topologico $ X $ composto dai punti $ \{a, b, c\} $, e adotto la topologia discreta su $ X $.

In questo spazio, tutti i sottoinsiemi di $ X $ sono aperti:

$ \emptyset $ e $ \{a, b, c\} $ sono aperti per definizione in $ X $ come insieme aperto.
I singoli punti $ \{a\} $, $ \{b\} $, $ \{c\} $ sono aperti perché nella topologia discreta ogni punto è un insieme aperto.
I sottoinsiemi formati da coppie di punti, come $ \{a, b\} $, $ \{a, c\} $, $ \{b, c\} $ , sono aperti perché sono unioni di insiemi aperti.

Considero l'insieme $ A = \{b, c\} $ nello spazio topologico $ X $.

Per la definizione di interno, $ \text{Int}(A) $ è l'unione di tutti gli insiemi aperti contenuti in $ A $.

Gli insiemi aperti contenuti in $ A $ sono $ \{b\} $, $ \{c\} $, e $ \{b, c\} $.

\[ Int(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Quindi, l'unione di questi insiemi aperti è $ \{b, c\} $, che è esattamente $ A $.

In conclusione, vale $ Int(A) = A $.

Nota. Questo risultato non è specifico per l'insieme $ A $; si applica a qualsiasi sottoinsieme $ S \subseteq X $ in uno spazio topologico discreto. L'interno di qualsiasi sottoinsieme è il sottoinsieme stesso. In generale, in uno spazio topologico discreto, dove ogni sottoinsieme è aperto, l'interno di qualsiasi insieme $ S $ è $ S $ stesso, ovvero $ Int(S) = S $.

Il teorema dell'interno di un insieme

Dato un sottoinsieme $ S $ dello spazio topologico $ X $ e un elemento $ y \in X $, l'elemento $ y $ appartiene all'interno del sottoinsieme $ \text{Int(S)} $ se e solo se esiste un insieme aperto $ U $ tale che $ y \in U \subset S $ $$ y \in \text{Int}(S) \iff \exists \ U \text{ aperto tale che } y \in U \subseteq A $$

Detto in altre parole, l'elemento y∈X per trovarsi nell'intorno dell'insieme S, deve appartenere anche a un insieme aperto U che è interamente contenuto in S.

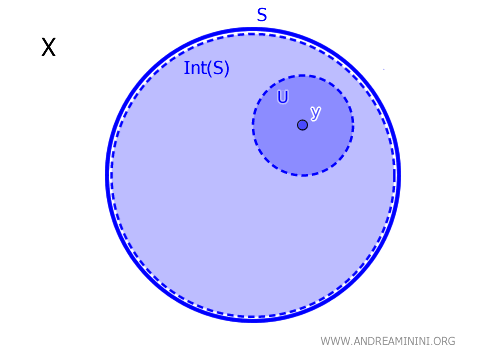
esempio visivo

Questo teorema stabilisce una condizione necessaria e sufficiente per determinare se un punto y si trova all'interno di un insieme S in uno spazio topologico X.

Dimostrazione

Condizione necessaria: Se $y$ è un elemento dell'interno di $S$, allora per definizione di interno, esiste un insieme aperto $U$ in $X$ tale che $y$ è in $U$ e $U$ è completamente contenuto in $S$. Questo mostra che se $y \in \operatorname{Int}(A)$, allora deve esistere tale $U$. Questo soddisfa la condizione del "solo se" nel teorema.
Condizione sufficiente: Se esiste un insieme aperto $U$ tale che $y \in U \subset S$, allora per definizione di insieme aperto e per il fatto che $U$ è contenuto in $S$, allora tutti i punti di $U$, incluso $y$, devono essere nell'interno di $S$ perché l'interno di $S$ è definito come l'unione di tutti gli insiemi aperti contenuti in $S$. Quindi, l'elemento $y$ deve appartenere a $\operatorname{Int}(S)$.

Nota. Questo teorema è utile perché collega direttamente la nozione di insieme aperto con la proprietà di essere all'interno di un insieme, che è centrale per studiare la continuità e altre proprietà topologiche degli spazi.

Esempio

Considero l'insieme $ A = [1, 3] $ dei numeri reali compresi nell'intervallo chiuso da 1 a 3 nello spazio topologico $ \mathbb{R} $ con la topologia standard.

$$ A = [1,3] $$

In pratica, sto considerando tutti i punti della retta da 1 a 3 inclusi.

Provo a determinare l'interno di $ A $ utilizzando il teorema dell'interno di un insieme.

Per trovare l'interno di $ A $, devo identificare un insieme aperto $ U $ tale che $ U \subset A $ e ogni punto in $ U $ appartiene anche a $ \operatorname{Int}(A) $.

Scelta di $ U $
Scelgo l'insieme $ U = (1, 3) $ ovvero l'intervallo aperto da 1 a 3 con gli estremi esclusi. Questo insieme è aperto nella topologia standard di $ \mathbb{R} $ perché è un intervallo aperto.
Verifica che $ U \subset A $
Osservo che ogni punto in $ U = (1, 3) $ è anche un punto di $ A = [1, 3] $. Non considero i punti estremi $ 1 $ e $ 3 $ poiché $ U $ è aperto e non include i suoi estremi.

Quindi, $ U $ è un insieme aperto ed è completamente contenuto in $ A $, il che significa che tutti i punti di $ U $ sono interni ad $ A $.

In questo caso, poiché solo gli estremi di $ A=[1,3] $ sono esclusi dall'insieme $ U = (1,3) $, deduco anche che $ \operatorname{Int}(A) = (1, 3) $.

Nota. Questo risultato mostra che l'interno di $ A $ è l'intervallo aperto $ (1, 3) $. I punti agli estremi $ 1 $ e $ 3 $ non sono inclusi in $ \operatorname{Int}(A) $ perché non esiste alcun intervallo aperto contenente questi punti che sia interamente contenuto in $ A $.

Le proprietà degli interni

Alcune proprietà relative all'interno di un insieme in uno spazio topologico. Ognuna di queste proprietà mostra una relazione interessante e non sempre intuitiva tra operazioni di base come l'interno, la chiusura, l'unione e l'intersezione in uno spazio topologico.

Proprietà dell'unione degli interni
L'unione degli interni di due insiemi è sempre contenuta nell'interno dell'unione dei due insiemi. Tuttavia, l'uguaglianza non vale sempre. $$ Int(A) ∪ Int(B) ⊆ Int(A ∪ B) $$
Proprietà di intersezione degli interni
L'intersezione degli interni di due insiemi è uguale all'interno dell'intersezione di quegli insiemi. $$ Int(A) ∩ Int(B) = Int(A ∩ B) $$
Proprietà di complementarità di interno e chiusura
L'interno del complemento di un insieme $A$ è uguale al complemento della chiusura di $A$. $$ Int(X - A) = X - Cl(A) $$
Proprietà di complementarità di chiusura e interno
La chiusura del complemento di un insieme $A$ è uguale al complemento dell'interno di $A$. $$ Cl(X - A) = X - Int(A) $$

Osservazioni

Alcune osservazioni e note aggiuntive

Se U è un insieme aperto in X e U ⊆ A, allora U ⊆ Int(A)
Se $ U $ è un insieme aperto in uno spazio topologico $ X $ e è completamente contenuto in un insieme $ A $, allora $ U $ è anche incluso nell'interno di $ A $. L'interno di $ A $, denotato come $ \text{Int}(A) $, è definito come il più grande insieme aperto contenuto in $ A $. Pertanto, qualsiasi insieme aperto $ U $ che si trova dentro $ A $ sarà automaticamente una parte dell'interno di $ A $.
Se A ⊆ B allora Int(A) ⊆ Int(B)
Se un insieme $ A $ è completamente contenuto in un insieme $ B $, allora l'interno di $ A $ è necessariamente contenuto nell'interno di $ B $. Questo perché qualsiasi insieme aperto contenuto in $ A $ sarà anche contenuto in $ B $. Di conseguenza, l'operazione di formare l'interno preserva l'inclusione tra insiemi.
L'insieme A è aperto se e solo se A = Int(A)
Un insieme $ A $ in uno spazio topologico $ X $ si definisce aperto se coincide con il suo interno. In altre parole, $ A $ è aperto se ogni punto in $ A $ ha un intorno aperto completamente contenuto in $ A $. Pertanto, $ A $ è aperto se e solo se $ A = \text{Int}(A) $, ovvero se contiene tutti gli insiemi aperti che può contenere all'interno di sé.

E così via.