La topologia degli insiemi aperti

In altre parole, la collezione T deve contenere al suo interno solo insiemi di X considerati "aperti" ed è chiusa alle operazioni di unione e intersezione.

Dove una collezione di insiemi è un insieme i cui elementi sono degli insiemi o sottoinsiemi.

In questi casi, l'insieme X e la topologia T formano uno spazio topologico che spesso si indica con la coppia (X,T). 

Nota. Spesso per semplificare si indica solo che X è uno spazio topologico. Basta però ricordarsi che uno spazio topologico è composto da due elementi: la topologia T (collezione di sottoinsiemi) e l'insieme X.

Perché l'insieme vuoto è sempre considerato un insieme aperto?

L'insieme vuoto è considerato aperto per definizione in ogni spazio topologico.

Questa convenzione fa parte delle definizioni fondamentali della topologia e serve a garantire che le proprietà e gli assiomi della topologia siano coerenti e completi.

Un esempio pratico

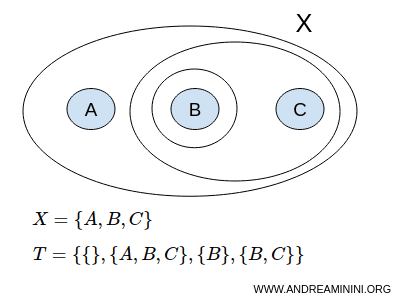
Considero un insieme X con tre elementi A, B, C

$$ X = \{ A,B,C \} $$

Una topologia T potrebbe essere la collezione di sottoinsiemi { }, {A,B,C}, {B}, {B,C}

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

Dove { } è l'insieme vuoto Ø e {A,B,C} è l'insieme stesso, ovvero i sottoinsiemi impropri dell'insieme X.

Per definizione l'insieme vuoto e l'insieme completo X sono insiemi aperti per definizione.

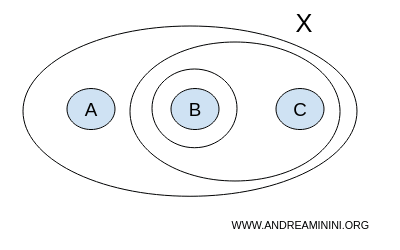
Una topologia deve essere composta da insiemi aperti e, per definizione, l'unione e l'intersezione di insiemi aperti genera un altro insieme aperto.

In questo caso l'unione dei sottoinsiemi considerati in T appartiene ancora alla collezione T.

Quindi, la collezione T è chiusa alle operazioni di unione.

$$ \{ B \} \cup \{ B, C \} ⊆ \{ B, C \} ⊆ T$$

$$ \{ B \} \cup \{ A, B, C \} ⊆ \{ A, B, C \} ⊆ T$$

$$ \{ B \} \cup \{ \  \} ⊆ \{ B \} ⊆ T $$

$$ \{ B \} \cup \{  B \} ⊆ \{ B \} ⊆ T$$

Inoltre, l'intersezione dei sottoinsiemi in T è ancora parte della collezione T.

Quindi, la collezione T è chiusa anche alle operazioni di intersezione.

$$ \{ B \} \cap \{ B, C \} ⊆ \{ B \} ⊆ T$$

$$ \{ B \} \cap \{ A, B, C \} ⊆ \{ B \} ⊆ T$$

$$ \{ B \} \cap \{ \ \} ⊆ \{ \ \} ⊆ T $$

$$ \{ B \} \cap \{  B \} ⊆ \{ B \} ⊆ T$$

Pertanto, la collezione T è una topologia dell'insieme X perché soddisfa tutte le condizioni necessarie.

Esempio 2

Considero una collezione leggermente diversa dal precedente esempio.

L'insieme X è sempre lo stesso.

$$ X = \{ A,B,C \} $$

In questo caso, però, nella collezione T c'è anche il sottoinsieme {A} oltre ai sottoinsiemi { }, {A,B,C}, {B}, {B,C}.

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

Questa nuova collezione T di sottoinsiemi non è una topologia, dell'insieme X perché non soddisfa tutte le condizioni.

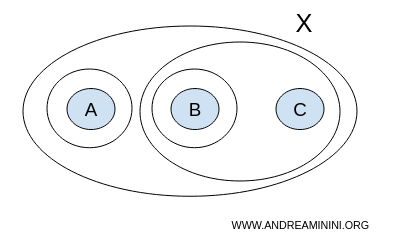
Ad esempio, l'unione dei sottoinsiemi {A} e {B} genera un insieme {A,B} che non è incluso nella collezione T stessa.

$$ \require{cancel}  \{ A \} \cup \{ B \} = \{ A, B \} \cancel{ \in } T  $$

In altre parole, i due insiemi {A} e {B} sono considerati insiemi "aperti" perché si trovano nella collezione T.

Tuttavia, la loro unione non genera un altro insieme aperto {A,B} perché l'insieme {A,B} non si trova nella collezione.

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

Questo viola una delle condizioni necessarie della topologia di un insieme aperto.

Pertanto, la collezione T non posso considerarla una topologia dell'insieme X. 

E così via