Le basi di una topologia

Le basi della topologia sono una collezione B di insiemi aperti tale che ogni insieme aperto nello spazio topologico T può essere ottenuto come unione di insiemi nella base B.

Considerato un insieme X e una collezione T di sottoinsiemi di X che definiscono una topologia su X, le basi della topologia T sono una collezione B di insiemi, detti elementi di base, che soddisfano le seguenti condizioni:

• Ogni elemento x dell'insieme X deve appartenere ad almeno un insieme contenuto in B.
• Ogni elemento x dell'insieme X presente nell'intersezione B₁⋂B₂ (non vuota) di una coppia di insiemi appartenenti a B, deve appartenere a un insieme B₃ contenuto nell'intersezione. In altre parole, l'elemento x è un elemento di base.
  

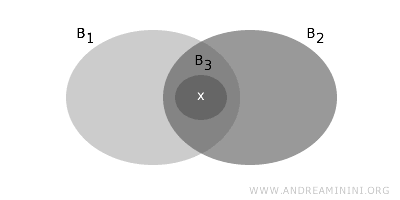
Queste condizioni mi garantiscono che la collezione di insiemi B sia una base della topologia T.

A cosa serve?

Le basi della topologia mi consentono di costruire la topologia T tramite l'unione di elementi di base, senza dover elencare ogni singolo insieme della collezione T.

Nota. La proprietà relativa alle intersezioni degli elementi di base mi assicura che la topologia soddisfi gli assiomi fondamentali, inclusa la condizione che l'intersezione di due insiemi aperti sia aperta.

Un esempio pratico

Considero l'insieme X

$$ \{a, b, c \} $$

e la topologia T

$$ T = \{ Ø, \{ a \}, \{ b,c \}, \{ a,b,c, \}  \} $$

In questo caso, T è l'insieme di tutti gli insiemi aperti in X, e ogni elemento di T è un insieme aperto per definizione.

Una base B per questa topologia potrebbe essere la seguente:

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

Queste basi soddisfano tutte le condizioni necessarie perché ogni elemento di X={a,b,c} è presente in un sottoinsieme di B e non ci sono intersezioni.

Nota che ogni insieme aperto in T può essere espresso come un'unione di insiemi in B.

Ad esempio, l'insieme {a} è già in B, l'insieme {b,c} è anch'esso in B, e l'intero spazio X può essere ottenuto unendo {a} e {b,c}.

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c, \}  = \{ a \} \cup \{ b,c \} $$

Nota. Nella teoria degli insiemi l'insieme vuoto Ø è un sottoinsieme improprio di qualsiasi insieme ed è sempre presente per definizione. Quindi, è presente anche in B. $$ Ø \in B $$ Inoltre, l'insieme vuoto è un insieme aperto per definizione in una topologia.

Questo esempio illustra il concetto di base di un insieme aperto in un contesto finito.

In contesti più complessi o infiniti, la definizione di base e la sua applicazione possono diventare più sofisticate, ma l'idea di fondo rimane la stessa: una base fornisce gli "elementi costruttivi" per tutti gli insiemi aperti dello spazio topologico.

Soluzione alternativa

Un'altra possibile base B della topologia sull'insieme X={a,b,c} è la seguente:

$$ B = \{ \{ a \} ,\{ b \}, \{ c \}  \} $$

In questo caso la base è composta dagli insiemi singoletti (singleton) degli elementi di X.

Verifico che B sia effettivamente una base per la topologia T={∅,X,{a},{b,c}}

• L'insieme vuoto ∅ è un insieme aperto per definizione e non richiede elementi per essere costruito. Inoltre è un sottoinsieme improprio di qualsiasi insieme ed è sempre presente.
• L'insieme {a} è già presente in B. $$ \{ a \} \in B $$
• L'insieme {b,c} può essere ottenuto dall'unione di {b} e {c}, entrambi presenti in B. $$ \{ b,c \}  = \{ b \} \cup \{ c \} $$
• L'intero insieme X={a,b,c} posso ottenerlo unendo tutti gli insiemi in B, ovvero {a}, {b}, e {c}. $$ \{ a,b,c \}  = \{ a \} \cup \{ b \} \cup \{ c \} $$

Quindi, B funziona come una base per la topologia su X perché mi permette di costruire tutti gli insiemi aperti di T mediante unioni degli insiemi in B.

Nota. Questo esempio dimostra come possano esistere diverse basi per la stessa topologia, ognuna delle quali fornisce un modo diverso di "generare" gli insiemi aperti della topologia attraverso unioni degli insiemi base.

Esempio 2

La base formata da tutti gli intervalli reali (a,b) con a<b genera tutti i punti della retta.

$$ B=\{ \ (a,b) \ ⊂ \ R \ | \ a<b \ \} $$

Si tratta di una base perché ogni punto della retta è compreso in un intervallo aperto (a,b).

Inoltre, se due intervalli aperti si intersecano, allora il punto che si trova nell'intersezione è contenuto in un altro insieme di B all'interno dell'intersezione.

Ad esempio, se considero due intervalli aperti (0, 3) e (2, 4), la loro intersezione è l'intervallo aperto (2,3).

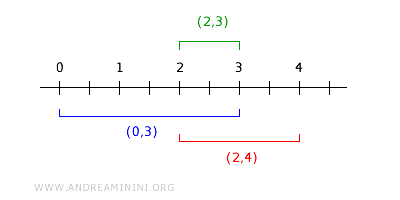
L'intervallo (2,3) a sua volta è un altro insieme B_i della base B e si trova all'interno dell'intersezione. $$ (0,3) \cap (2,4) = (2,3) ∈  B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

Teorema

Una collezione di insiemi aperti C in uno spazio topologico (X, T) è una base per la topologia T se per ogni insieme aperto U in T e per ogni punto x∈U, c'è un insieme V nella collezione C che contiene x e che è completamente contenuto in U. $$ x \in V \subset U $$

Un esempio

Considero la topologia T nell'insieme X composta dall'insieme vuoto, dall'insieme dei numeri reali R e da tutti gli intervalli (-∞, p) per ogni p di R.

Questa è una base della topologia T perché contiene l'insieme vuoto, sia l'unione che l'intersezione sono a loro volta degli insiemi aperti.

Devo verificare se per qualsiasi numero razionale q di Q, la collezione di insiemi C={(−∞,q)⊂R} è una base della topologia (X,T).

Considero un generico insieme aperto U={−∞,p} di T.

Per qualsiasi elemento x∈U contenuto nell'insieme U, posso scegliere un numero razionale tale che x>q>p.

Questo mi assicura che:

• L'elemento x è contenuto nell'intervallo (−∞,q) che è un insieme aperto V={−∞,q} della collezione C, poiché x<q. $$ x \in V={−∞,q} \subset C $$
• L'insieme V={−∞,q} è completamente contenuto nell'insieme U={−∞,p} della topologia T, poiché p>q

Pertanto, la collezione C={(−∞,q)⊂R} è una base della topologia (X,T).

Osservazioni

Alcune osservazioni aggiuntive sulle basi di una topologia

• Se considero un insieme X e costruisco una base B in cui ogni elemento x∈X è un insieme {x}∈B nelle basi, ottengo le basi di qualsiasi topologia T sull'insieme X.

  In generale, l'unione dei singoletti (singleton) mi permette di ottenere qualsiasi topologia.
  
  Ad esempio, la base B={ {a}, {b}, {c} } nel caso dell'insieme X={a,b,c} genera la topologia T={Ø,{a},{b,c},X}
  
  La stessa base B può generare qualsiasi altra topologia su X come la topologia T={Ø,{b},{a,c},X}. la topologia banale T={Ø, X} o la topologia discreta T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X}, ecc.

  Nota. La prima condizione è soddisfatta perché ogni elemento di X si trova in un insieme di B. Anche la seconda condizione è soddisfatta perché gli insiemi {x} sono insiemi disgiunti per costruzione, essendo ogni insieme composto da un singolo elemento dell'insieme X.

E così via.