La topologia standard di un insieme aperto
La topologia standard su R considera come insieme aperto ogni intervallo (a,b) con a<b e l'unione, sia finita che infinita, di intervalli aperti (a,b).
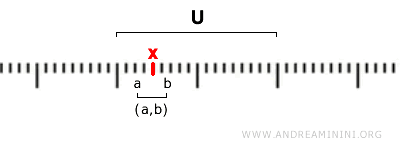
Questo significa che un insieme U è aperto se ogni punto x in U ha almeno un intervallo aperto (a,b) tale che x appartiene a (a,b) e (a,b)⊆U.
$$ x \in (a,b) \subseteq U $$
In altre parole, ogni elemento x dell'insieme aperto U si trova in un intervallo (a,b) che appartiene ancora all'insieme U.
Quindi, nella topologia standard sono insiemi aperti i seguenti:
- Intervalli aperti
Gli insiemi aperti nella topologia standard su \( \mathbb{R} \) sono definiti come intervalli aperti \( (a, b) \), con a<b, e qualsiasi unione, sia finita che infinita, di intervalli aperti \( (a, b) \). - Operazioni sugli insiemi sperti
Sono insiemi aperti anche le unioni e le intersezioni degli insiemi aperti
- Unioni: L'unione di qualsiasi numero di insiemi aperti, indipendentemente da quanto sia grande il numero, è sempre un insieme aperto.
- Intersezioni finite: L'intersezione di un numero finito di insiemi aperti è anche un insieme aperto.
Va detto che la topologia standard è solo una tra le molteplici topologie che possono essere definite su un insieme aperto X, ma a causa della sua rilevanza e frequenza d'uso in molte aree della matematica, viene denominata "standard".
La scelta di questa topologia non è arbitraria, dipende dalla sua utilità nel rappresentare concetti intuitivi di vicinanza, apertura e continuità, in particolare, della retta reale R.
Nota. Le topologie alternative su R o su altri insiemi possono avere basi diverse, che a loro volta generano insiemi aperti secondo regole diverse dalla topologia standard. In genere, sono definite per studiare proprietà diverse o per esplorare situazioni matematiche sotto una luce nuova.
Esempio pratico
La topologia standard di una retta reale R consiste in una base composta da tutti gli intervalli aperti (a,b) con a<b.
$$ B = \{ (a,b) ⊂ R \ \ | \ \ a<b \} $$
La caratteristica chiave qui è che per ogni punto x all'interno di un intervallo, posso trovare un piccolo intervallo aperto attorno a quel punto che è completamente contenuto nell'intervallo originale, il che soddisfa la definizione di insieme aperto nella topologia standard.
$$ \forall \ x \ \in U \ \exists \ ε>0 \ | \ x \in (x-ε ,x+ε ) \subseteq U $$
Dove U è un insieme aperto della topologia standard nell'insieme R.
Questa topologia è detta "standard" perché è la più comunemente utilizzata sulla retta reale.
Esempio 2
Considero l'intervallo di numeri reali (0,1) compreso tra 0 e 1 esclusi e la topologia standard.
Devo verificare se formano uno spazio topologico.
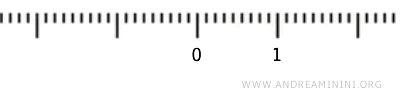
In pratica, un insieme \( U \subset (0, 1) \) è aperto in \( (0, 1) \) se per ogni punto \( x \in U \), esiste un intervallo aperto \( (a, b) \) in \( \mathbb{R} \) tale che \( x \in (a, b) \) e \( (a, b) \cap (0, 1) \subseteq U \).
In questo caso, però, basta osservare che l'intervallo (0,1) è un'intersezione tra gli insiemi aperti della topologia standard in R.
Quindi, l'intervallo \( (0, 1) \) è uno spazio topologico con la topologia indotta dalla topologia standard di \( \mathbb{R} \).
Ad esempio, \( (0.1, 0.5) \), \( (0.2, 0.9) \), o l'unione di tali intervalli, come \( (0.1, 0.5) \cup (0.6, 0.8) \), sono tutti insiemi aperti in \( (0, 1) \) secondo la topologia indotta. In altre parole, gli insiemi aperti all'interno di \( (0, 1) \) sono quelli già compresi in R, ma confinati all'interno di \( (0, 1) \).
Poiché \( (0, 1) \) è un sottospazio di \( \mathbb{R} \) con la topologia indotta, conserva tutte le proprietà di base di un spazio topologico.
Esempio 3
Considero l'insieme finito X={1,2,3} composto da tre numeri interi.
Devo verificare se forma uno spazio topologico con la topologia standard di $ \mathbb{R} $.
In questo caso, i singoli elementi di X non sono insiemi aperti, perché la topologia standard di \( \mathbb{R} \) si riferisce agli intervalli aperti come base per gli insiemi aperti, il che non è applicabile direttamente all'insieme \( X \).
Ad esempio, se considero l'elemento {2} dell'insieme X come numero reale questo è compreso in un intervallo aperto (2-ε,2+ε) ma i punti di questo intervallo sono altri numeri reali che non appartengono all'insieme X. Quindi, la definizione di insieme aperto della topologia standard in R non è soddisfatta.
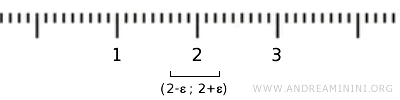
Considerando \( X \) come un sottoinsieme di \( \mathbb{R} \) potrei adottare la "topologia indotta" o "topologia di sottospazio" su \( X \) ma in questo caso gli insiemi aperti sarebbero solo l'insieme vuoto e l'insieme \( X \) stesso, e non sarebbe una situazione molto interessante dal punto di vista topologico.
Per costruire uno spazio topologico con gli insiemi finiti come \( X \) è preferibile adottare la topologia discreta, dove ogni sottoinsieme di \( X \) è considerato un insieme aperto per definizione.
E così via
