Analisi dello spettro di frequenza e fase

Per analizzare lo spettro di un segnale periodico seguo alcune regole e convenzioni pratiche.

1. L'angolo di fase è misurato rispetto al coseno. Pertanto, le eventuali componenti seno devono essere convertite in coseno. $$ \sin at = \cos (at - 90°) $$
2. L'ampiezza A del coseno deve essere positiva. Le eventuali ampiezze -A cos wt devono essere trasformate in A cos (wt ±180°). $$ -A \cos wt = A \cos (wt ±180°) $$ La scelta +180° o -180° è indifferente.
3. L'argomento (angolo) del coseno deve essere indicati sulla base di 2π. Questo permette di rappresentare lo spettro delle ampiezze e delle fasi.

Un esempio pratico

Ho il seguente segnale

$$ w(t) = 7 - 10 \cos (40 \pi t - 60°)+4 \sin 120 \pi t $$

Trasformo le costanti in termini di frequenza zero

$$ w(t) = 7 \cos 2 \pi 0t - 10 \cos (40 \pi t - 60°)+4 \sin 120 \pi t $$

Converto l'ampiezza negativa in positiva aggiungendo +180°

$$ w(t) = 7 \cos 2 \pi 0t + 10 \cos (40 \pi t - 60° + 180°)+4 \sin 120 \pi t $$

$$ w(t) = 7 \cos 2 \pi 0t + 10 \cos (40 \pi t + 120°) + 4 \sin 120 \pi t $$

Trasformo il seno in coseno riducendo l'argomento di -90°

$$ w(t) = 7 \cos 2 \pi 0t + 10 \cos (40 \pi t + 120°) + 4 \cos (120 \pi t -90°) $$

Nota. La forma d'onda del segnale nel dominio del tempo è la seguente

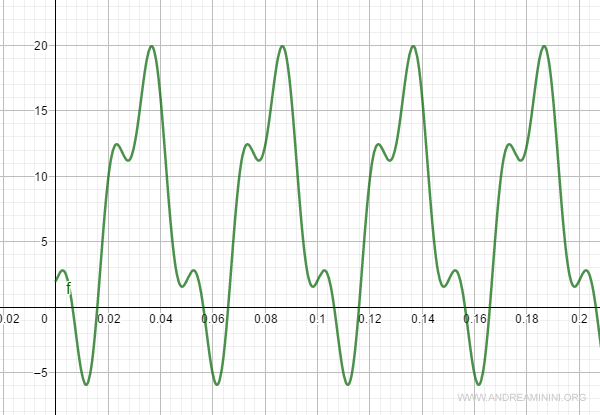
Analisi dello spettro di frequenze

Trasformo gli argomenti in 2π

$$ w(t) = 7 \cos 2 \pi 0t + 10 \cos (2 \pi \cdot 20 \cdot t + 120°) + 4 \cos (2 \pi \cdot 60 \cdot t -90°) $$

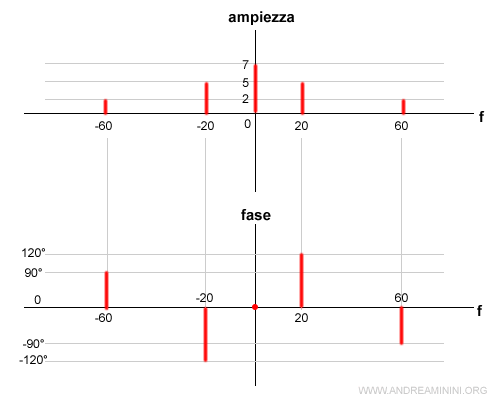
In questo modo posso associare le ampiezze ( 7, 10, 4) delle componenti del segnale alle relative frequenze (0, 20, 60).

Questo mi permette di analizzare lo spettro delle frequenze rispetto all'ampiezza e alla fase.

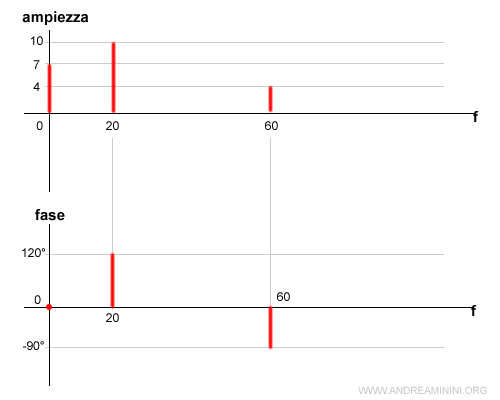
Analisi dello spettro di frequenze con i fasori

Per rappresentare lo spettro di frequenze del segnale tramite i fasori, uso la regola seguente

$$ \cos ω_0t+φ = \frac{A}{2} \cdot e^{iφ}e^{iω_0t} + \frac{A}{2} \cdot e^{-iφ}e^{-iω_0t } $$

Questa regola mette in relazione la parte reale del segnale sul piano di Gauss con il fasore

$$ w(t) = 7 \cos 2 \pi 0t + 10 \cos (2 \pi \cdot 20 \cdot t + 120°) + 4 \cos (2 \pi \cdot 60 \cdot t -90°) $$

Per semplificare la spiegazione suddiviso il segnale in tre parti

$$ 7 \cos 2 \pi 0t $$ $$ 10 \cos (2 \pi \cdot 20 \cdot t + 120°) $$ $$ 4 \cos (2 \pi \cdot 60 \cdot t -90°) $$

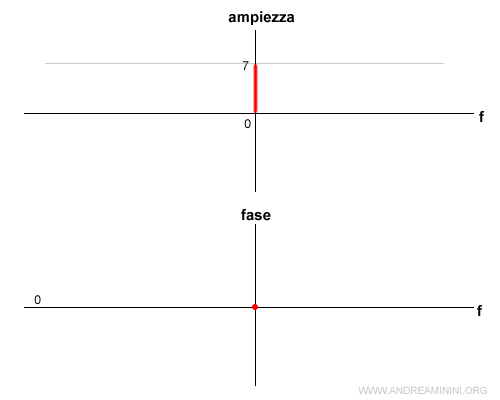
Trasformo la prima componente 7 cos(2π·0·t) in fasore.

In questo caso A=7, ω₀=0, φ=0

$$ 7 \cos 2 \pi 0t = \frac{7}{2} \cdot e^{i \cdot 0}e^{i \cdot 0 \cdot t} + \frac{7}{2} \cdot e^{-i \cdot 0}e^{-i \cdot 0 \cdot t } $$

Questa forma mi permette di ottenere i dati positivi e negativi delle frequenze.

In questo caso coincidono perché ω₀=0, φ=0

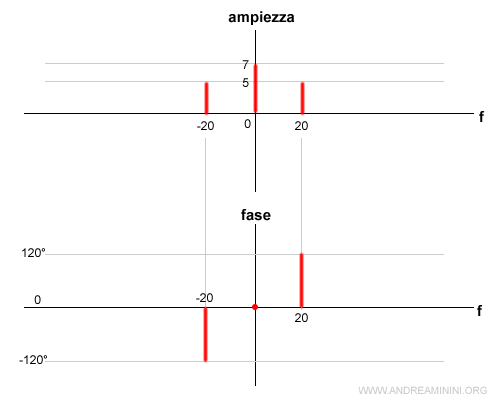
Trasformo la seconda componente 10 cos(2π·20·t + 120°) in fasore.

In questo caso A=10, ω₀=20, φ=120°

$$ 10 \cos 2 \pi \cdot 20 \cdot t + 120° = \frac{10}{2} \cdot e^{i \cdot 120°}e^{i \cdot 20 \cdot t} + \frac{10}{2} \cdot e^{-i \cdot 120°}e^{-i \cdot 20 \cdot t } $$

$$ 10 \cos 2 \pi \cdot 20 \cdot t + 120° = 5 \cdot e^{120° \cdot i}e^{ 20 \cdot i \cdot t} + 5 \cdot e^{-120° \cdot i}e^{-20 \cdot i \cdot t } $$

Questa forma mi permette di ottenere i dati positivi e negativi delle frequenze.

Il fasore (primo termine) è A=5, φ=120° e ω₀=20

Il fasore coniguato (secondo termine) è A=5, φ=-120° e ω₀=-20

Trasformo la terza componente 4 cos(2π·60·t - 90°) in fasore.

In questo caso A=4, ω₀=60, φ=-90°

$$ 4 \cos 2 \pi \cdot 60 \cdot t - 90° = \frac{4}{2} \cdot e^{i \cdot (-90°)}e^{i \cdot 60 \cdot t} + \frac{4}{2} \cdot e^{-i \cdot (-90°)}e^{-i \cdot 60 \cdot t } $$

$$ 4 \cos 2 \pi \cdot 60 \cdot t - 90° = 2 \cdot e^{-90°i }e^{60 \cdot i \cdot t} + 2 \cdot e^{-90°i}e^{-60 \cdot i \cdot t } $$

Il fasore (primo termine) è A=2, φ=-90° e ω₀=60

Il fasore coniguato (secondo termine) è A=2, φ=90° e ω₀=-60

E così via.