La varianza

La varianza è un indicatore della dispersione di una variabile o distribuzione statistica che ottengo calcolando la media dei quadrati degli scarti della media aritmetica (μ). $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$

Nel caso delle distribuzioni di frequenza la formula della varianza è la seguente

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - \mu )^2 \cdot n_i $$

Dove μ è la media aritmetica mentre n_i sono le frequenze.

La varianza si basa sulla proprietà che la somma dei quadrati degli scarti dalla media è minima, ovvero è la più bassa possibile.

Se calcolassi la somma dei quadrati degli scarti da un valore diverso dalla media, otterrei un valore maggiore.

Nota. La varianza è espressa tramite il quadrato dell'unità di misura delle osservazioni. Ad esempio, se le osservazioni sono misure in metri, la varianza è una misura in metri al quadrato. Pertanto, non posso rappresentare la varianza e la distribuzione di dati in un unico diagramma.

Un esempio pratico

Esempio 1

Considero una distribuzione di valori composta da n=6 elementi

$$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$

La media aritmetica della distribuzione statistica è uguale a μ=5

$$ \mu = \frac{1+5+7+3+6+8}{6 } = \frac{30}{6 } = 5 $$

Per misurare la dispersione intorno alla media calcolo la varianza

$$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$

Sapendo che n=6 e μ=5

$$ \sigma^2 = \frac{1}{6} \cdot \sum_{i=1}^n (x_i - 5 )^2 $$

Sviluppo la serie di valori x₁=1, x₂=5, x₃=7, x₄=3, x₅=6, x₆=8

$$ \sigma^2 = \frac{1}{6} \cdot [ (1- 5 )^2+(5- 5 )^2+(7- 5 )^2+(3- 5 )^2+(6- 5 )^2+(8- 5 )^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ (-4 )^2+(0 )^2+(2)^2+(-2)^2+(1)^2+(3)^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ 16+0+4+4+1+9] $$

$$ \sigma^2 = \frac{34}{6} $$

Pertanto, la varianza della distribuzione è σ^₂=5,66

$$ \sigma^2 = 5,66 $$

Esempio 2

Considero questa distribuzione di frequenze

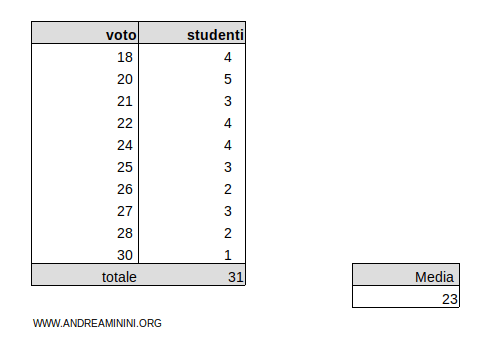
La media aritmetica ponderata dei dati è μ=23

In questo caso, per calcolare la varianza uso la formula delle distribuzioni di frequenze

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - \mu )^2 \cdot n_i $$

Nella tabella ci sono k=10 classi e la media dei dati è μ=23

$$ \sigma^2 = \frac{1}{\sum_i^{10} n_i} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

La somma delle frequenze Σn_i=31

$$ \sigma^2 = \frac{1}{31} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

Sviluppo il calcolo dei quadrati degli scarti degli elementi x₁=18, x₂=20, x₃=21, x₄=22, x₅=24, x₆=25, x₇=26, x₈=27, x₉=28, x₁₀=30 rispetto alla media ponderata μ=23

$$ \sigma^2 = \frac{(18 - 23 )^2 \cdot 4 + (20 - 23 )^2 \cdot 5 + (21 - 23 )^2 \cdot 3 + (22 - 23 )^2 \cdot 4 + (24 - 23 )^2 \cdot 4 + \\ + (25 - 23 )^2 \cdot 3 + (26 - 23 )^2 \cdot 2 + (27 - 23 )^2 \cdot 3 + (28 - 23 )^2 \cdot 2 + (30- 23 )^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{(-5)^2 \cdot 4 + (-3)^2 \cdot 5 + (-2)^2 \cdot 3 + (-1)^2 \cdot 4 + (1)^2 \cdot 4 + \\ + (2)^2 \cdot 3 + (3)^2 \cdot 2 + (4)^2 \cdot 3 + (5)^2 \cdot 2 + (7)^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{25 \cdot 4 +9 \cdot 5 + 4 \cdot 3 +1 \cdot 4 + 1 \cdot 4 +4 \cdot 3 + 9 \cdot 2 + 16 \cdot 3 + 25 \cdot 2 + 49 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{100 +45 + 12 +4 + 4 +12 + 18 + 48 + 50+ 49 }{31} $$

$$ \sigma^2 = \frac{342}{31} $$

Pertanto, la varianza della distribuzione di frequenze è σ^₂=11,03

$$ \sigma^2 = 11,03 $$

Osservazioni

Alcune osservazioni utili sulla varianza

• La varianza non ha la stessa unità di misura del fenomeno osservato
  La varianza è pari al quadrato dell'unità di misura del fenomeno osservato. Ad esempio, se il fenomeno è misurato in metri (m), la varianza del fenomeno è misurata in metri al quadrato (m²). Pertanto, non posso confrontare, né rappresentare i dati in un unico sistema di riferimento o diagramma.
• Un modo alternativo per calcolare la varianza
  Posso calcolare la varianza anche come differenza tra il quadrato della media quadratica (μ_q)e il quadrato della media aritmetica (μ) della distribuzione $$ \sigma^2 = \mu_q^2 - \mu^2 $$ In alternativa, posso calcolare la varianza anche tramite la differenza tra la media aritmetica dei quadrati dei valori (x₁²,x₂²,...,x_n²)/n e il quadrato della media aritmetica (μ²) $$ \sigma^2 = \frac{x_1^2+x_2^2+...+x_n^2}{n} - \mu^2 $$
  

  Esempio. Considero la distribuzione dell'esempio precedente $$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$ Di questa conosco già la media aritmetica μ=5 e la varianza σ²=5,66. Calcolo la media quadratica della distribuzione $$ \mu_q = \sqrt{ \frac{1^2+5^2+7^2+3^2+6^2+8^2}{6} } $$ $$ \mu_q = \sqrt{ \frac{1+25+49+9+36+64}{6} } $$ $$ \mu_q = \sqrt{ \frac{184}{6} } = \sqrt{ 30,66} = 5,538 $$ A questo punto conosco la media aritmetica μ=5 e la media quadratica μ_q=5,538. Calcolo la varianza come differenza tra il quadrato della media quadratica e il quadrato della media aritmetica $$ \sigma^2 = \mu_q^2 - \mu^2 $$ $$ \sigma^2 = 5,538^2 - 5^2 $$ $$ \sigma^2 = 30,66 - 25 $$ $$ \sigma^2 = 5,66 $$ Il risultato finale è lo stesso. La varianza della distribuzione è σ²=5,66.

  Dimostrazione. La formula della varianza è $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$ Svolgo il quadrato del binomio $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i^2 -2 x_i \mu + \mu^2) $$ Applico le proprietà delle serie numeriche $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - \sum_{i=1}^n 2 x_i \mu + \sum_{i=1}^n \mu^2) \ ] $$ Sapendo che 2μ è un termine costante, applico nuovamente le proprietà delle serie e lo faccio uscire dalla seconda serie $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \mu \sum_{i=1}^n x_i + \sum_{i=1}^n \mu^2) \ ] $$ La terza serie posso riscriverla come Σμ²=nμ² $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \mu \cdot ( \sum_{i=1}^n x_i ) + n \mu^2 \ ] $$ La media aritmetica posso riscriverla come μ=Σx_i/n $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot ( \frac{1}{n} \sum_{i=1}^n x_i ) \cdot ( \sum_{i=1}^n x_i ) + n \mu^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} ( \sum_{i=1}^n x_i )^2 + n \mu^2 \ ] $$ L'ultimo termine lo riscrivo come nμ²=n(Σx_i/n)² $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} ( \sum_{i=1}^n x_i )^2 + n ( \frac{1}{n} \cdot \sum_{i=1}^n x_i )^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 + n \cdot \frac{1}{n^2} \cdot \sum_{i=1}^n x_i^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 + \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 - \frac{1}{n} \cdot \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 \ $$ $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 - \frac{1}{n^2} \cdot \sum_{i=1}^n x_i ^2 $$ $$ \sigma^2 = ( \frac{1}{n} \cdot \sum_{i=1}^n x_i^2) - (\frac{1}{n} \cdot \sum_{i=1}^n x_i) ^2 $$ Il primo termine è la media quadratica al quadrato (μ_q)² mentre il secondo termine è la media aritmetica al quadrato μ². Il risultato è quello che volevo dimostrare $$ \sigma^2 = \mu_q^2 - \mu^2 $$

• La correzione di Sheppard
  Quando la distribuzione è suddivisa in classi il raggruppamento causa un'approssimazione nel calcolo della varianza. Per ridurre l'approssimazione si utilizza la correzione di Sheppard. $$ \sigma^2_R = \sigma^2 - \frac{ \alpha^2 }{12} $$ Dove σ² è la varianza e α è l'ampiezza delle classi.

  Nota. Una certa approssimazione nel calcolo si presenta in tutti gli indicatori quando il fenomeno è suddiviso in classi ma è molto più marcato nella varianza perché la misura della varianza è il quadrato dell'unità di misura del fenomeno osservato.

E così via.